Abstract
We address the problem of proof-search in the natural deduction calculus for Intuitionistic propositional logic. Our aim is to improve the usual proof-search procedure where introduction rules are applied upwards and elimination rules downwards. In particular, we introduce \(\mathbf {Nbu} \), a variant of the usual natural deduction calculus for Intuitionistic Propositional Logic, and we show that it can be used as a base for a goal-oriented proof-search procedure. We also show that the implementation of our proof-search procedure is competitive with those based on sequent or tableaux calculi.








Similar content being viewed by others
Notes
The derivations and their LaTeX rendering are generated with nbu, an implementation of our proof-search procedure available at http://www.dista.uninsubria.it/~ferram/.
Differently from the examples discussed in previous sections, open \(\mathbf {Nbu} \)-trees corresponding to failed derivations are not explicitly built, but are implicitly represented by the recursion tree.
\(\texttt {nbu} \) is a available at http://github.com/ferram/jtabwb_provers/.
The provers have been tested with the following configurations: \(\mathtt {fCube}\) v 11.1 and \(\mathtt {intuit}\) with no options; \(\mathtt {IntHistGC}\) with options -b -c -c3; \(\mathtt {Imogen}\) with options prop prove -h optimize.
The problem set, named randomXX, is available at http://github.com/ferram/jtabwb_ipl_problems.
References
Brock-Nannestad, T., Schürmann, C.: Focused natural deduction. In: Fermüller, C.G., Voronkov, A. (eds.) LPAR-17, LNCS, vol. 6397, pp. 157–171. Springer, Berlin (2010)
Chagrov, A., Zakharyaschev, M.: Modal Logic. Oxford University Press, Oxford (1997)
Claessen, K., Rosén, D.: SAT modulo intuitionistic implications. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR-20, vol. 9450, pp. 622–637. Springer, Berlin (2015)
Dyckhoff, R., Lengrand, S.: A strongly focused calculus for intuitionistic logic. In: Beckmann, A., Berger, U., Löwe, B., Tucker, J.V. (eds.) CiE, LNCS, vol. 3988, pp. 173–185. Springer, Berlin (2006)
Dyckhoff, R., Pinto, L.: Permutability of inferences in intuitionistic sequent calculi. Technical Report CS/97/7, University of St Andrews (1997)
Dyckhoff, R., Pinto, L.: Cut-elimination and a permutation-free sequent calculus for intuitionistic logic. Stud. Log. 60(1), 107–118 (1998)
Dyckhoff, R., Pinto, L.: Permutability of proofs in intuitionistic sequent calculi. Theor. Comput. Sci. 212(1–2), 141–155 (1999)
Englander, C., Dowek, G., Haeusler, E.H.: Yet another bijection between sequent calculus and natural deduction. Electron. Notes Theor. Comput. Sci. 312, 107–124 (2015)
Ferrari, M., Fiorentini, C.: Proof-search in natural deduction calculus for classical propositional logic. In: Nivelle, H.D. (ed.) TABLEAUX 2015, LNCS, vol. 9323, pp. 237–252. Springer, Berlin (2015)
Ferrari, M., Fiorentini, C., Fiorino, G.: FCube: an efficient prover for intuitionistic propositional logic. In: Fermüller, C.G., Voronkov, A. (eds.) LPAR-17, LNCS, vol. 6397, pp. 294–301. Springer, Berlin (2010)
Ferrari, M., Fiorentini, C.: Simplification rules for intuitionistic propositional tableaux. ACM Trans. Comput. Log. TOCL 13(2), 14:1–14:23 (2012)
Ferrari, M., Fiorentini, C., Fiorino, G.: A terminating evaluation-driven variant of G3i. In: Galmiche, D., Larchey-Wendling, D. (eds.) TABLEAUX 2013, LNCS, vol. 8123, pp. 104–118. Springer, Berlin (2013)
Ferrari, M., Fiorentini, C., Fiorino, G.: An evaluation-driven decision procedure for G3i. ACM Trans. Comput. Log. TOCL 16(1), 8:1–8:37 (2015)
Ferrari, M., Fiorentini, C., Fiorino, G.: JTabWb: a Java framework for implementing terminating sequent and tableau calculi. Fundam. Inf. 150, 119–142 (2017)
Gentzen, G., Gentzen, G.: Investigations into logical deduction. In: Szabo, M. (ed.) The Collected Works of Gerhard Gentzen, pp. 68–131. North-Holland, Amsterdam (1969)
Goré, R., Thomson, J., Wu, J.: A history-based theorem prover for intuitionistic propositional logic using global caching: IntHistGC system description. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) Automated Reasoning—7th International Joint Conference, IJCAR 2014, LNCS, vol. 8562, pp. 262–268. Springer, Berlin (2014)
Herbelin, H.: A lambda-calculus structure isomorphic to Gentzen-style sequent calculus structure. In: Pacholski, L., Tiuryn, J. (eds.) CSL, LNCS, vol. 933, pp. 61–75. Springer, Berline (1994)
Heuerding, A., Seyfried, M., Zimmermann, H.: Efficient loop-check for backward proof search in some non-classical propositional logics. In: Miglioli, P., Moscato, U., Mundici, D., Ornaghi, M. (eds.) TABLEAUX, LNCS, vol. 1071, pp. 210–225. Springer, Berlin (1996)
Howard, W.: The formulae-as-types notion of construction. In: Seldin, J., Hindley, J. (eds.) To H.B. Curry: Essay on Combinatory Logic, Lambda-calculus and Formalism. Kluwer Academic Publishers, Hingham (1980)
Howe, J.: Proof search issues in some non-classical logics. Ph.D. thesis, School of Mathematical and Computational Sciences, University of St Andrews (1998)
Howe, J.W.: Two loop detection mechanisms: a comparison. In: Galmiche, D. (ed.) TABLEAUX 1997, LNCS, vol. 1227, pp. 188–200. Springer, Berlin (1997)
Liang, C., Miller, D.: On focusing and polarities in linear logic and intuitionistic logic (2008). http://www.lix.polytechnique.fr/~dale/papers/focusli.pdf
Liang, C., Miller, D.: Focusing and polarization in linear, intuitionistic, and classical logics. Theor. Comput. Sci. 410(46), 4747–4768 (2009)
McLaughlin, S., Pfenning, F.: Imogen: focusing the polarized inverse method for intuitionistic propositional logic. In: Cervesato, I., Veith, H., Voronkov, A. (eds.) LPAR-15, LNCS, vol. 5330, pp. 174–181. Springer, Berlin (2008)
Miller, D., Nadathur, G., Pfenning, F., Scedrov, A.: Uniform proofs as a foundation for logic programming. Ann. Pure Appl. Log. 51, 125–157 (1991)
Mints, G., Steinert-Threlkeld, S.: ADC method of proof search for intuitionistic propositional natural deduction. J. Log. Comput. 26(1), 395–408 (2016)
Pfenning, F.: Automated theorem proving. Lecture notes, Carnegie Mellon University (2004)
Prawitz, D.: Natural Deduction. Almqvist and Wiksell, Stockholm (1965)
Raths, T., Otten, J., Kreitz, C.: The ILTP problem library for intuitionistic logic. J. Autom. Reason. 31, 261–271 (2007)
Sahlin, D., Franzén, T., Haridi, S.: An intuitionistic predicate logic theorem prover. J. Log. Comput. 2(5), 619–656 (1992)
Santo, J.E.: The lambda-calculus and the unity of structural proof theory. Theory Comput. Syst. 45(4), 963–994 (2009)
Savnik, I.: Index data structure for fast subset and superset queries. In: Cuzzocrea, A., Kittl, C., Simos, D.E., Weippl, E., Xu, L. (eds.) Availability, Reliability, and Security in Information Systems and HCI, LNCS, vol. 8127, pp. 134–148. Springer, Berlin (2013)
Sieg, W., Byrnes, J.: Normal natural deduction proofs (in classical logic). Stud. Log. 60(1), 67–106 (1998)
Sieg, W., Cittadini, S.: Normal natural deduction proofs (in non-classical logics). In: Hutter, D., Stephan, W. (eds.) Mechanizing Mathematical Reasoning, LNCS, vol. 2605, pp. 169–191. Springer, Berlin (2005)
Troelstra, A., Schwichtenberg, H.: Basic proof theory. In: Cambridge Tracts in Theoretical Computer Science (2nd ed.), vol. 43. Cambridge University Press (2000)
Acknowledgements
We thank the anonymous reviewers for their valuable remarks which helped us to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
A Completeness of \(\mathbf {NI} \)
We prove the completeness of \(\mathbf {NI} \) (Theorem 2). We start from the calculus \(\mathbf {NI}_0 \) introduced in [5, 7, 27] to build derivations in normal form for \(\mathrm {IPL} \). Rules of \(\mathbf {NI}_0 \) are the same as \(\mathbf {NI} \) (see Fig. 2), except that \(\downarrow \!\uparrow ^{}\), \(\bot E\) and \(\vee E\) are applied without restrictions (p, F and D are any formulas). By the Normalization Theorem of natural deduction calculus of \(\mathrm {IPL} \) we get:
Theorem 8
(Completeness of \(\mathbf {NI}_0 \)) \(A\in \mathrm {IPL} \) iff  . \(\square \)
. \(\square \)
In order to prove the completeness of \(\mathbf {NI} \), we introduce the calculus \(\mathbf {NI}_1 \), obtained from \(\mathbf {NI}_0 \) by imposing on \(\downarrow \!\uparrow ^{}\) and \(\bot E\) the same restrictions as in \(\mathbf {NI} \) (see Fig. 2). Note that \(\mathbf {NI}_1 \)-derivations correspond to derivations in “long normal form”.
Let \(\rho \) be the reduction on \(\mathbf {NI}_0 \)-derivations defined in Fig. 9; given an \(\mathbf {NI}_0 \)-derivation \(\mathscr {D}\) of \(\sigma \), \(\rho (\mathscr {D})\) is an \(\mathbf {NI}_0 \)-derivation of \(\sigma \) obtained from \(\mathscr {D}\) by replacing an application of \(\mathscr {R}\in \{\!\downarrow \!\uparrow ^{},\bot E\}\) with one or more application of \(\mathscr {R}\) to smaller formulas. By repeatedly applying \(\rho \), we eventually get an \(\mathbf {NI}_0 \)-derivation \(\mathscr {E}\) of \(\sigma \) which is an \(\mathbf {NI}_1 \)-derivation. This proves that:
Lemma 17
\(\mathbf {NI}_0 \vdash \sigma \) implies \(\mathbf {NI}_1 \vdash \sigma \). \(\square \)
By the completeness of \(\mathbf {NI}_0 \) and Lemma 17, the completeness of \(\mathbf {NI}_1 \) follows:
Theorem 9
(Completeness of \(\mathbf {NI}_1 \)) \(A\in \mathrm {IPL} \) iff  . \(\square \)
. \(\square \)
To complete the proof of the completeness of \(\mathbf {NI} \), we have to map \(\mathbf {NI}_1 \) into \(\mathbf {NI} \). Let \(\mathscr {D}\) be an \(\mathbf {NI}_1 \)-derivation and let \(\mathscr {C}^{\vee E}(\mathscr {D})\) be the multiset collecting all the sequents which occur in \(\mathscr {D}\) as the conclusion of an applications of \(\vee E\). The \(\vee \)-rank of \(\mathscr {D}\), denoted by \(\mathrm {Rnk}^{\vee }(\mathscr {D})\), is defined as follows:

Note that, if \(\mathrm {Rnk}^{\vee }(\mathscr {D})=0\), then every application of \(\vee E\) in \(\mathscr {D}\) has a conclusion either of the form  , with \(F\in {\mathscr {V}} \cup \{\bot \}\), or of the form
, with \(F\in {\mathscr {V}} \cup \{\bot \}\), or of the form  , hence \(\mathscr {D}\) is an \(\mathbf {NI} \)-derivation. In the next lemma we show how we can reduce the \(\vee \)-rank of an \(\mathbf {NI}_1 \)-derivation.
, hence \(\mathscr {D}\) is an \(\mathbf {NI} \)-derivation. In the next lemma we show how we can reduce the \(\vee \)-rank of an \(\mathbf {NI}_1 \)-derivation.
Lemma 18
Let \(\mathscr {D}\) be an \(\mathbf {NI}_1 \)-derivation of \(\sigma \) such that \(\mathrm {Rnk}^{\vee }(\mathscr {D})=k\) and \(k >0\). Then, there exists an \(\mathbf {NI}_1 \)-derivation of \(\sigma \) having \(\vee \)-rank bounded by \(k-1\).
Proof
Since \(\mathrm {Rnk}^{\vee }(\mathscr {D})>0\), \(\mathscr {D}\) contains at least a subderivation \(\mathscr {E}\) of the form

such that:
-
\(H=H_1\wedge H_2\) or \(H= H_1\rightarrow H_2\)
-
\(\mathrm {Rnk}^{\vee }(\mathscr {E}_0) \,=\, \mathrm {Rnk}^{\vee }(\mathscr {E}_1)\,=\, \mathrm {Rnk}^{\vee }(\mathscr {E}_2)\,=\,0\).
Note that \(\mathrm {Rnk}^{\vee }(\mathscr {E})=|H|\). We build an \(\mathbf {NI}_1 \)-derivation \(\mathscr {F}\) of  such that \(\mathrm {Rnk}^{\vee }(\mathscr {F}) \le |H|-1\). By replacing in \(\mathscr {D}\) the subderivation \(\mathscr {E}\) with \(\mathscr {F}\), we get an \(\mathbf {NI}_1 \)-derivation of \(\sigma \) having \(\vee \)-rank at most \(k-1\).
such that \(\mathrm {Rnk}^{\vee }(\mathscr {F}) \le |H|-1\). By replacing in \(\mathscr {D}\) the subderivation \(\mathscr {E}\) with \(\mathscr {F}\), we get an \(\mathbf {NI}_1 \)-derivation of \(\sigma \) having \(\vee \)-rank at most \(k-1\).
Let \(H=H_1\wedge H_2\). Since \(\mathrm {Rnk}^{\vee }(\mathscr {E}_1)=0\) and \(\mathrm {Rnk}^{\vee }(\mathscr {E}_2)=0\), the root rule of \(\mathscr {E}_1\) and \(\mathscr {E}_2\) must be an application of \(\wedge I\). Thus, \(\mathscr {E}\) has the form

We build \(\mathscr {F}\) as follows:

The case \(H=H_1\rightarrow H_2\) is similar. In this case \(\mathscr {E}\) has the form

and we define \(\mathscr {F}\) as follows

\(\square \)
By repeatedly applying Lemma 18, we can transform an \(\mathbf {NI}_1 \)-derivation of \(\sigma \) into an \(\mathbf {NI}_1 \)-derivation of \(\sigma \) having \(\vee \)-rank 0, namely into an \(\mathbf {NI} \)-derivation of \(\sigma \). By the completeness of \(\mathbf {NI}_1 \) (Theorem 9), it follows that \(A\in \mathrm {IPL} \) iff  , and this proves the completeness of \(\mathbf {NI} \) (Theorem 2).
, and this proves the completeness of \(\mathbf {NI} \) (Theorem 2).
B The Isomorphism Between \(\mathbf {Nbu} \) and \(\mathbf {LJTbu} \)
We define a 1-1 translation from \(\mathbf {Nbu} \)-derivations to \(\mathbf {LJTbu} \)-derivations, where \(\mathbf {LJTbu} \) is the sequent calculus obtained by adding labels b, u to Herbelin calculus \(\mathbf {LJT} \) (see Sect. 7). Following [6,7,8, 20], we introduce two maps \(\psi \) and \(\psi '\), where I-rules are translated bottom-up and E-rules top-down, and we show that they admit inverse maps \(\theta \) and \(\theta '\) respectively.
An \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) is \(\uparrow \)-reduced if the root rule of \(\mathscr {T}\) is one among \(\downarrow \!\uparrow ^{}\), \(\bot E\), \(\vee E\). Let \(\mathscr {T}\) be an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree with root sequent \(\sigma _r\); then, \(\sigma _r\) has the form  , where \(D\in {\mathscr {V}} \cup \{\bot \}\) or \(D=D_0\vee D_1\). The main branch of an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) is its left-most branch, namely the branch containing the major premises of rule applications. Note that, except for the root sequent \(\sigma _r\), every sequent \(\sigma \) in the main branch of \(\mathscr {T}\) has the form
, where \(D\in {\mathscr {V}} \cup \{\bot \}\) or \(D=D_0\vee D_1\). The main branch of an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) is its left-most branch, namely the branch containing the major premises of rule applications. Note that, except for the root sequent \(\sigma _r\), every sequent \(\sigma \) in the main branch of \(\mathscr {T}\) has the form  and it is either a leaf of \(\mathscr {T}\) or the conclusion of one of the rules \(\mathrm {Id} \), \(\wedge E_k\), \(\rightarrow E\). By the notation
and it is either a leaf of \(\mathscr {T}\) or the conclusion of one of the rules \(\mathrm {Id} \), \(\wedge E_k\), \(\rightarrow E\). By the notation

we indicate an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) such that  is the root sequent of \(\mathscr {T}\),
is the root sequent of \(\mathscr {T}\),  is an open assumption on the main branch of \(\mathscr {T}\) and \(\mathscr {T}\) has no other open assumption. To translate \(\mathbf {Nbu} \) into \(\mathbf {LJTbu} \), we define the maps \(\psi \) and \(\psi '\) by mutual induction, so that the following properties hold:
is an open assumption on the main branch of \(\mathscr {T}\) and \(\mathscr {T}\) has no other open assumption. To translate \(\mathbf {Nbu} \) into \(\mathbf {LJTbu} \), we define the maps \(\psi \) and \(\psi '\) by mutual induction, so that the following properties hold:
-
(P1)
Let \(\mathscr {D}\) be an \(\mathbf {Nbu} \)-derivation of
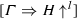 . Then, \(\psi (\mathscr {D})\) is an \(\mathbf {LJTbu} \)-derivation of
. Then, \(\psi (\mathscr {D})\) is an \(\mathbf {LJTbu} \)-derivation of 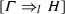 .
. -
(P2)
Let \(\mathscr {T}\) be the \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree
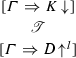
Then, \(\psi '(\mathscr {T})\) is an \(\mathbf {LJTbu} \)-derivation of
 .
.
The maps \(\psi \) and \(\psi '\) are defined in Figs. 10 and 11 respectively. The latter case in Fig. 10 defines the application of \(\psi \) to an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-derivation \(\mathscr {D}\). Note that the derivation \(\mathscr {D}\) is obtained by applying the rule \(\mathrm {Id} \) to the open assumption of the \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree

Since  is in \(\mathscr {D}\) an axiom sequent, it holds that \(A\in \varGamma \). To compute \(\psi (\mathscr {D})\), we firstly apply \(\psi '\) to \(\mathscr {T}_0\), yielding by (P2) an \(\mathbf {LJTbu} \)-derivation of
is in \(\mathscr {D}\) an axiom sequent, it holds that \(A\in \varGamma \). To compute \(\psi (\mathscr {D})\), we firstly apply \(\psi '\) to \(\mathscr {T}_0\), yielding by (P2) an \(\mathbf {LJTbu} \)-derivation of  . Since \(A\in \varGamma \), we can apply \(\mathrm {Cont} \) to get
. Since \(A\in \varGamma \), we can apply \(\mathrm {Cont} \) to get  . The map \(\psi '\) destructures an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) with the open assumption \(\sigma \) in the main branch, starting from \(\sigma \) and moving downwards. The base cases (first three cases in Fig. 11) occur when \(\sigma \) is a premise of the root rule of \(\mathscr {T}\). Otherwise, \(\sigma \) must be a premise of \(\mathscr {R}\in \{\wedge E_k,\rightarrow E\}\) and we inductively apply \(\psi '\) to the subtree of \(\mathscr {T}\) having the conclusion of \(\mathscr {R}\) as open assumption. One can immediately check that (P1) and (P2) hold.
. The map \(\psi '\) destructures an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) with the open assumption \(\sigma \) in the main branch, starting from \(\sigma \) and moving downwards. The base cases (first three cases in Fig. 11) occur when \(\sigma \) is a premise of the root rule of \(\mathscr {T}\). Otherwise, \(\sigma \) must be a premise of \(\mathscr {R}\in \{\wedge E_k,\rightarrow E\}\) and we inductively apply \(\psi '\) to the subtree of \(\mathscr {T}\) having the conclusion of \(\mathscr {R}\) as open assumption. One can immediately check that (P1) and (P2) hold.
Now, we define the maps \(\theta \) and \(\theta '\), corresponding to the inverse of \(\psi \) and \(\psi '\) respectively, so that the following properties hold:
-
(T1)
Let \(\mathscr {E}\) be an \(\mathbf {LJTbu} \)-derivation of
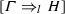 . Then, \(\theta (\mathscr {E})\) is an \(\mathbf {Nbu} \)-derivation of
. Then, \(\theta (\mathscr {E})\) is an \(\mathbf {Nbu} \)-derivation of 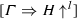 .
. -
(T2)
Let \(\mathscr {E}\) be an \(\mathbf {LJTbu} \)-derivation of
 . Then, \(\theta '(\mathscr {E})\) is an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) of the form
. Then, \(\theta '(\mathscr {E})\) is an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) of the form 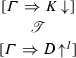
The maps \(\theta \) and \(\theta '\) are defined in Figs. 12 and 13 respectively. In the latter case of Fig. 12, by applying \(\theta '\) to \(\mathscr {E}_0\) we get an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-tree \(\mathscr {T}\) having the open assumption  in the main branch and no other open assumption. Note that, since rule \(\mathrm {Cont} \) has been applied at the root of \(\mathscr {E}\), \(A\in \varGamma \). To turn \(\mathscr {T}\) into an \(\mathbf {Nbu} \)-derivation, we can apply \(\mathrm {Id} \) to \(\sigma \). The following facts can be easily checked:
in the main branch and no other open assumption. Note that, since rule \(\mathrm {Cont} \) has been applied at the root of \(\mathscr {E}\), \(A\in \varGamma \). To turn \(\mathscr {T}\) into an \(\mathbf {Nbu} \)-derivation, we can apply \(\mathrm {Id} \) to \(\sigma \). The following facts can be easily checked:
-
(1)
\(\theta (\psi (\mathscr {D}))\,=\,\mathscr {D}\), where \(\mathscr {D}\) is an \(\mathbf {Nbu} \)-derivation;
-
(2)
\(\theta '(\psi '(\mathscr {T}))\,=\,\mathscr {T}\), where \(\mathscr {T}\) is an \(\uparrow \)-reduced \(\mathbf {Nbu} \)-derivation with an open assumption in the main branch;
-
(3)
\(\psi (\theta (\mathscr {E})) \,=\,\mathscr {E}\), where \(\mathscr {E}\) is an \(\mathbf {LJTbu} \)-derivation of
 ;
; -
(4)
\(\psi '(\theta '(\mathscr {E})) \,=\,\mathscr {E}\), where \(\mathscr {E}\) is an \(\mathbf {LJTbu} \)-derivation of
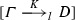 .
.
Accordingly, \(\theta =\psi ^{-1}\) and \(\theta '=\psi '^{-1}\). We conclude that \(\psi \) is a 1-1 map between \(\mathbf {Nbu} \) and \(\mathbf {LJTbu} \).
Rights and permissions
About this article
Cite this article
Ferrari, M., Fiorentini, C. Goal-Oriented Proof-Search in Natural Deduction for Intuitionistic Propositional Logic. J Autom Reasoning 62, 127–167 (2019). https://doi.org/10.1007/s10817-017-9427-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-017-9427-3











 ;
; 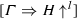 . Then,
. Then, 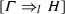 .
.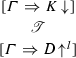
 .
.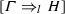 . Then,
. Then, 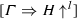 .
. . Then,
. Then, 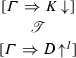
 ;
;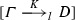 .
.