Abstract
The notion of a monad cannot be expressed within higher-order logic (HOL) due to type system restrictions. I show that if a monad is restricted to values of a fixed type, this notion can be formalised in HOL. Based on this idea, I develop a library of effect specifications and implementations of monads and monad transformers. Hence, I can abstract over the concrete monad in HOL definitions and thus use the same definition for different (combinations of) effects. I illustrate the usefulness of effect polymorphism with a monadic interpreter.
Similar content being viewed by others
Notes
Available in the Archive of Formal Proofs at https://www.isa-afp.org/entries/Monomorphic_Monad.html.
Type variables that appear in the signature of locale parameters are fixed for the whole locale. In particular, the value type
 cannot be instantiated inside the locale
cannot be instantiated inside the locale
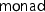 or its extension
or its extension
 . The interpreter
. The interpreter
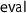 , however, returns
, however, returns
 s. For this reason,
s. For this reason,
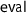 is defined in an extension of
is defined in an extension of
 that merely specialises
that merely specialises
 to
to
 . For readability, I usually omit this detail in this article.
. For readability, I usually omit this detail in this article.Continuation parameters like
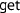 ’s and
’s and
 ’s make it possible to circumvent the restriction to monomorphic values. More generally, if we made every definition take a continuation, like in continuation-passing style, we would regain value polymorphism. In doing so, we would however lose that sequencing of computations and control flow is captured by a small number of (primitive) operations. Instead, every definition could implement arbitrary control flow, like in a continuation monad. Thus, we would need a lot more lemmas to reason about sequencing. In a commutative monad, e.g., one commutativity lemma would be needed for every pair of definitions. In contrast, my approach needs just one assumption comm to express commutativity of sequencing (Sect. 2.5), and a few assumptions about the primitive operations, e.g., sample-comm (Sect. 2.3).
’s make it possible to circumvent the restriction to monomorphic values. More generally, if we made every definition take a continuation, like in continuation-passing style, we would regain value polymorphism. In doing so, we would however lose that sequencing of computations and control flow is captured by a small number of (primitive) operations. Instead, every definition could implement arbitrary control flow, like in a continuation monad. Thus, we would need a lot more lemmas to reason about sequencing. In a commutative monad, e.g., one commutativity lemma would be needed for every pair of definitions. In contrast, my approach needs just one assumption comm to express commutativity of sequencing (Sect. 2.5), and a few assumptions about the primitive operations, e.g., sample-comm (Sect. 2.3).In my monad implementations in Sect. 3, sampling is relationally parametric for arbitrary relations
 , so I could drop the restriction
, so I could drop the restriction
 . However, this would unnecessarily exclude some other implementations as all my abstract proofs so far used only
. However, this would unnecessarily exclude some other implementations as all my abstract proofs so far used only
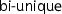 relations.
relations.The support of
 is the set of elementary events with positive probability:
is the set of elementary events with positive probability:
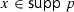 iff
iff

The conference paper [23] demanded sample-cong instead of sample-param. Parametricity is a better condition as it allows us to rename choices like in the biased coin flip example above.
Such environments can be nicely handled by adding a reader monad transformer (Sect. 4).
Isabelle’s
 feature, which resolves overloading during type checking, cannot be used either as it does not support recursive resolutions. For example, resolving
feature, which resolves overloading during type checking, cannot be used either as it does not support recursive resolutions. For example, resolving
 takes two steps: first to
takes two steps: first to
 and then to
and then to
 . The second step fails due to the intricate interleaving of type checking and resolution. Even if this is just an implementation issue, resolving overloading during type checking prevents definitions that are generic in the monad, which general overloading supports.
. The second step fails due to the intricate interleaving of type checking and resolution. Even if this is just an implementation issue, resolving overloading during type checking prevents definitions that are generic in the monad, which general overloading supports.Following the “as abstract as possible” spirit of this paper, I actually proved the identities in the locale of commutative monads and showed that
 is commutative if its inner monad is.
is commutative if its inner monad is.The alternative applicative interface [16] with the operator
 is amenable to monomorphisation if we restrict ourselves to infinite value types
is amenable to monomorphisation if we restrict ourselves to infinite value types
 as then
as then
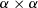 is isomorphic to
is isomorphic to
 . This interface is tailored towards a first-order language [10]. So functions must be uncurried and their arguments encoded using the isomorphism. We would thus clutter the definitions and proofs with conversions and lose the benefits of built-in higher-order unification.
. This interface is tailored towards a first-order language [10]. So functions must be uncurried and their arguments encoded using the isomorphism. We would thus clutter the definitions and proofs with conversions and lose the benefits of built-in higher-order unification.
References
Back, R.J., Wright, J.: Refinement Calculus—A Systematic Introduction. Springer, Berlin (1998)
Ballarin, C.: Locales: a module system for mathematical theories. J. Autom. Reason. 52(2), 123–153 (2014). https://doi.org/10.1007/s10817-013-9284-7
Blanchette, J.C., Hölzl, J., Lochbihler, A., Panny, L., Popescu, A., Traytel, D.: Truly modular (co)datatypes for Isabelle/HOL. In: ITP 2014. LNCS, vol. 8558, pp. 93–110. Springer (2014)
Bulwahn, L., Krauss, A., Haftmann, F., Erkök, L., Matthews, J.: Imperative functional programming with Isabelle/HOL. In: TPHOLs 2008. LNCS, vol. 5170, pp. 134–149. Springer (2008). https://doi.org/10.1007/978-3-540-71067-7_14
Eberl, M., Hölzl, J., Nipkow, T.: A verified compiler for probability density functions. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 80–104. Springer (2015). https://doi.org/10.1007/978-3-662-46669-8_4
Erwig, M., Kollmansberger, S.: Functional pearls: probabilistic functional programming in Haskell. J Funct Program 16, 21–34 (2006). https://doi.org/10.1017/S0956796805005721
Gibbons, J., Hinze, R.: Just do it: simple monadic equational reasoning. In: ICFP 2011, pp. 2–14. ACM (2011). https://doi.org/10.1145/2034773.2034777
Grimm, N., Maillard, K., Fournet, C., Hriţcu, C., Maffei, M., Protzenko, J., Ramananandro, T., Rastogi, A., Swamy, N., Zanella Béguelin, S.: A monadic framework for relational verification: applied to information security, program equivalence, and optimizations. In: CPP 2018, pp. 130–145. ACM (2018). https://doi.org/10.1145/3167090
Harrison, W.L.: The essence of multitasking. In: Johnson, M., Vene, V. (eds.) Algebraic Methodology and Software Technology (AMAST 2006). LNCS, vol. 4019, pp. 158–172. Springer (2006). https://doi.org/10.1007/11784180_14
Hinze, R.: Lifting operators and laws. http://www.cs.ox.ac.uk/ralf.hinze/Lifting.pdf. Accessed 12 June 2018 (2010)
Hölzl, J., Lochbihler, A., Traytel, D.: A formalized hierarchy of probabilistic system types. In: ITP 2015. LNCS, vol. 9236, pp. 203–220. Springer (2015). https://doi.org/10.1007/978-3-319-22102-1_13
Homeier, P.V.: The HOL-Omega logic. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 244–259. Springer (2009). https://doi.org/10.1007/978-3-642-03359-9_18
Huffman, B.: Formal verification of monad transformers. In: ICFP 2012, pp. 15–16. ACM (2012). https://doi.org/10.1145/2364527.2364532
Huffman, B., Kunčar, O.: Lifting and Transfer: a modular design for quotients in Isabelle/HOL. In: CPP 2013. LNCS, vol. 8307, pp. 131–146. Springer (2013). https://doi.org/10.1007/978-3-319-03545-1_9
Huffman, B., Matthews, J., White, P.: Axiomatic constructor classes in Isabelle/HOLCF. In: Hurd, J., Melham, T. (eds.) TPHOLs. LNCS, vol. 3603, pp. 147–162. Springer (2005). https://doi.org/10.1007/11541868_10
Hutton, G.: Higher-order functions for parsing. J. Funct. Program. 2(3), 323–343 (1992)
Jeuring, J., Jansson, P., Amaral, C.: Testing type class laws. In: Haskell 2012, pp. 49–60. ACM (2012). https://doi.org/10.1145/2364506.2364514
Kunčar, O.: Correctness of Isabelle’s cyclicity checker: implementability of overloading in proof assistants. In: CPP 2015, pp. 85–94. ACM (2015). https://doi.org/10.1145/2676724.2693175
Lammich, P., Tuerk, T.: Applying data refinement for monadic programs to Hopcroft’s algorithm. In: ITP 2012. LNCS, vol. 7406, pp. 166–182. Springer (2012). https://doi.org/10.1007/978-3-642-32347-8_12
Liang, S., Hudak, P., Jones, M.: Monad transformers and modular interpreters. In: POPL 1995, pp. 333–343. ACM (1995). https://doi.org/10.1145/199448.199528
Lobo Vesga, E.: Hacia la formalización del razonamiento ecuacional sobre mónadas. Technical report, Universidad EAFIT (2013). http://hdl.handle.net/10784/4554
Lochbihler, A.: Probabilistic functions and cryptographic oracles in higher order logic. In: Thiemann, P. (ed.) ESOP. LNCS, vol. 9632, pp. 503–531. Springer (2016). https://doi.org/10.1007/978-3-662-49498-1_20
Lochbihler, A.: Effect polymorphism in higher-order logic (proof pearl). In: Ayala-Rincón, M., Muñoz, C.A. (eds.) Interactive Theorem Proving (ITP 2017), vol. 10499, pp. 389–409. Springer (2017). https://doi.org/10.1007/978-3-319-66107-0_25
Lochbihler, A., Schneider, J.: Equational reasoning with applicative functors. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 252–273. Springer (2016). https://doi.org/10.1007/978-3-319-43144-4_16
Mitchell, J.C.: Representation independence and data abstraction. In: POPL 1986, pp. 263–276. ACM (1986). https://doi.org/10.1145/512644.512669
Moggi, E.: An abstract view of programming languages. Technical report ECS-LFCS-90-113, LFCS, School of Informatics, University of Edinburgh (1990)
Nipkow, T., Klein, G.: Concrete semantics. Springer, Berlin (2014). https://doi.org/10.1007/978-3-319-10542-0
Nipkow, T., Paulson, L.C.: Proof pearl: defining functions over finite sets. In: Hurd, J., Melham, T. (eds.) TPHOLs 2005. LNCS, vol. 3603, pp. 385–396. Springer (2005)
Piróg, M., Gibbons, J.: The coinductive resumption monad. In: Mathematical Foundations of Programming Semantics (MFPS 2014). ENTCS, vol. 308, pp. 273–288 (2014). https://doi.org/10.1016/j.entcs.2014.10.015
Ramsey, N., Pfeffer, A.: Stochastic lambda calculus and monads of probability distributions. In: POPL 2002, pp. 154–165. ACM (2002). https://doi.org/10.1145/503272.503288
Reynolds, J.C.: Types, abstraction and parametric polymorphism. In: IFIP 1983. Information Processing, vol. 83, pp. 513–523. North-Holland/IFIP (1983)
Sternagel, C., Thiemann, R.: A framework for developing stand-alone certifiers. In: Ayala-Rincón, M., Mackie, I. (eds.) Logical and Semantic Frameworks with Applications (LSFA 2014), vol. 312, pp. 51–67. ENTCS (2015). https://doi.org/10.1016/j.entcs.2015.04.004
Wadler, P.: How to replace failure by a list of successes: a method for exception handling, backtracking, and pattern matching in lazy functional languages. In: Jouannaud, J.P. (ed.) Functional Programming Languages and Computer Architecture (FPCA 1985). LNCS, vol. 201, pp. 113–128. Springer (1985). https://doi.org/10.1007/3-540-15975-4_33
Wadler, P.: Monads for functional programming. In: Jeuring, J., Meijer, E. (eds.) Advanced Functional Programming. LNCS, vol. 925, pp. 24–52. Springer (1995). https://doi.org/10.1007/3-540-59451-5_2
Wenzel, M.: Type classes and overloading in higher-order logic. In: Gunter, E.L., Felty, A. (eds.) TPHOLs 1997. LNCS, vol. 1275, pp. 307–322. Springer (1997). https://doi.org/10.1007/BFb0028402
Wimmer, S., Hu, S., Nipkow, T.: Verified memoization and dynamic programming. In: Avigad, J., Mahboubi, A. (eds.) Interactive theorem proving. ITP 2018. LNCS, vol. 10895, pp. 579–596. Springer, Cham (2018)
Acknowledgements
I thank Dmitriy Traytel and the anonymous reviewers for suggesting many improvements to the presentation. This work is supported by the Swiss National Science Foundation Grant 153217 “Formalising Computational Soundness for Protocol Implementations”.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article extends the conference version presented at Interactive Theorem Proving 2017 [23]. Most of this work was done while the author was at the Institute of Information Security at ETH Zurich, Zurich, Switzerland.
Appendix A: Step-By-Step Proof of Lemma memo-idem
Appendix A: Step-By-Step Proof of Lemma memo-idem
Proof
First, I prove that updating the table of memoised calls is idempotent. Let
 . Then,
. Then,
 holds:
holds:

Next, let

Then,

Rights and permissions
About this article
Cite this article
Lochbihler, A. Effect Polymorphism in Higher-Order Logic (Proof Pearl). J Autom Reasoning 63, 439–462 (2019). https://doi.org/10.1007/s10817-018-9476-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-018-9476-2





 cannot be instantiated inside the locale
cannot be instantiated inside the locale
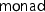 or its extension
or its extension
 . The interpreter
. The interpreter
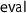 , however, returns
, however, returns
 s. For this reason,
s. For this reason,
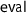 is defined in an extension of
is defined in an extension of
 that merely specialises
that merely specialises
 to
to
 . For readability, I usually omit this detail in this article.
. For readability, I usually omit this detail in this article.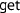 ’s and
’s and
 ’s make it possible to circumvent the restriction to monomorphic values. More generally, if we made every definition take a continuation, like in continuation-passing style, we would regain value polymorphism. In doing so, we would however lose that sequencing of computations and control flow is captured by a small number of (primitive) operations. Instead, every definition could implement arbitrary control flow, like in a continuation monad. Thus, we would need a lot more lemmas to reason about sequencing. In a commutative monad, e.g., one commutativity lemma would be needed for every pair of definitions. In contrast, my approach needs just one assumption
’s make it possible to circumvent the restriction to monomorphic values. More generally, if we made every definition take a continuation, like in continuation-passing style, we would regain value polymorphism. In doing so, we would however lose that sequencing of computations and control flow is captured by a small number of (primitive) operations. Instead, every definition could implement arbitrary control flow, like in a continuation monad. Thus, we would need a lot more lemmas to reason about sequencing. In a commutative monad, e.g., one commutativity lemma would be needed for every pair of definitions. In contrast, my approach needs just one assumption  , so I could drop the restriction
, so I could drop the restriction
 . However, this would unnecessarily exclude some other implementations as all my abstract proofs so far used only
. However, this would unnecessarily exclude some other implementations as all my abstract proofs so far used only
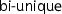 relations.
relations. is the set of elementary events with positive probability:
is the set of elementary events with positive probability:
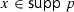 iff
iff

 feature, which resolves overloading during type checking, cannot be used either as it does not support recursive resolutions. For example, resolving
feature, which resolves overloading during type checking, cannot be used either as it does not support recursive resolutions. For example, resolving
 takes two steps: first to
takes two steps: first to
 and then to
and then to
 . The second step fails due to the intricate interleaving of type checking and resolution. Even if this is just an implementation issue, resolving overloading during type checking prevents definitions that are generic in the monad, which general overloading supports.
. The second step fails due to the intricate interleaving of type checking and resolution. Even if this is just an implementation issue, resolving overloading during type checking prevents definitions that are generic in the monad, which general overloading supports. is commutative if its inner monad is.
is commutative if its inner monad is. is amenable to monomorphisation if we restrict ourselves to infinite value types
is amenable to monomorphisation if we restrict ourselves to infinite value types
 as then
as then
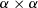 is isomorphic to
is isomorphic to
 . This interface is tailored towards a first-order language [
. This interface is tailored towards a first-order language [