Inhibition enhances memory capacity: optimal feedback, transient replay and oscillations

Abstract

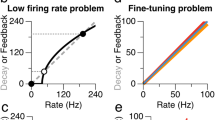
Recurring sequences of neuronal activation in the hippocampus are a candidate for a neurophysiological correlate of episodic memory. Here, we discuss a mean-field theory for such spike sequences in phase space and show how they become unstable when the neuronal network operates at maximum memory capacity. We find that inhibitory feedback rescues replay of the sequences, giving rise to oscillations and thereby enhancing the network’s capacity. We further argue that transient sequences in an overloaded network with feedback inhibition may provide a mechanistic picture of memory-related neuronal activity during hippocampal sharp-wave ripple complexes.

Appendix: First and second moments

The dynamics underlying neuronal activity sequences is formulated as a two-dimensional iterated map in Eqs. (2)–(6). This time-discrete dynamics is simplified using Gaussian approximations for the distributions of the number h of synaptic inputs to a specified neuron. The Gaussian approximation therefore requires expressions for the means and variances of the input sums h.

Inputs can be of two kinds, hits m and false alarms n. The input sum $h=\sum_{j=1}^{m+n}w_{j}\, s_{j}$ thus runs over all m + n ≤ N active (firing) neurons in the network and depends on two binary random variables for each potential input: w ∈ {0,1} indicating the presence of a synaptic connection, and s ∈ {0,1} indicating its state (Gibson and Robinson 1992). The stochasticity of s is inherited from the randomness of the activity patterns underlying the memory sequences via Willshaw’s learning rule.

The distribution of w is given by the morphological connectivity such that prob(w = 1) = c _m . The probability prob(s = 1) of a synapse having been potentiated depends on whether it connects or not neurons that should fire in sequence at the particular point in time.

The Willshaw rule ensures that synapses that connect sequentially firing neurons are in the potentiated state, i.e. prob(s = 1) = 1, and thus for this subset of synapses the input sum depends on a binomial process with probability prob(w = 1) = c _m .

For the other synapses, the probability prob(s = 1) = q _x depends on the the number x ≤ P of associations the specific postsynaptic neuron is involved in. Note that if the postsynaptic neuron is never supposed to fire, the Willshaw rule will activate none of its synapses and thus q ₀ = 0. In general, the probability that a neuron is not a target in one specific step of the sequence (association) is 1 − f, and thus the probability that it is not a target in any one of x associations is (1 − f)^x. Conversely, the probability of such a synapse being potentiated is $q_{x}=1-(1-f)^{x}$. Hence, assuming independence of the two binomial processes, the input sum h for this subset of synapses is binomial with probability

$${\rm prob}(w_{i}\, s_{i}=1)=c_{m}\, q_{x}\ .\label{eq-pwa} $$

(11)

The probability distribution of the input h can then be determined as

$$ p(h)=\sum\limits_{x=0}^{P}p(h|x)\, p(x)\ ,\label{eq-ph} $$

(12)

in which the conditional probability $p(h|x)=\binom{m+n}{h}\,(c_{m}\ q_{x})^{h}\,(1-c_{m} q_{x})^{m+n-h}$ is derived from Eq. (11), and the probability p(x) that a neuron is involved in x associations is also binomial, viz. $p(x)=\binom{P}{x}\, f^{x}\,(1-f)^{P-x}$.

To compute expected values of h, we have to discern between neurons that should be active at time step t + 1 (and are supposed to generate the hits) and those that should be silent (and potentially give rise to false alarms). For the potential false alarms, we obtain

$$\begin{array}{rll} \langle h\rangle_{\rm Of\/f} &=& \sum\limits_{h=0}^{m+n} h \sum\limits_{x=0}^P p(h|x)\, p(x) =\sum\limits_{x=0}^Pp(x)\sum\limits_{h=0}^{m+n} h\, p(h|x) \\ &=&\sum\limits_{x=0}^P p(x)\, (m+n)\, (c_m\, q_x)\\ &=& (m+n)\, c_m \sum\limits_{x=0}^P [1-(1-f)^x]\,\binom{P}{x} f^{x} (1-f)^{P-x}\\ &=& (m+n)\, c_m \left[ 1 - (1-f)^P \sum\limits_{x=0}^P\binom{P}{x} f^{x}\right] \\ &=&(m+n)\, c_m \left[ 1 - (1-f)^P\, (1+f)^P\right]\\ &=&(m+n)\, c\ . \end{array}$$

Note that the last step makes use of the capacity of the Willshaw rule, Eq. (1). Similarly, for the potential hits, we obtain

$$\begin{array}{rll} \langle h\rangle_{\rm On} &=& \sum\limits_{h'=0}^{n} h' \sum\limits_{x=0}^P p(h'|x)\, p(x) + \sum\limits_{h''=0}^{m} h''\, p(h'')\\ &=& n\, c + m\, c_m\ . \end{array}$$

Here the expected value sums over two independent subsets of neurons, the first one (h′) representing the false alarms, and the second (h′′) representing the hits during the previous time step.

The corresponding variances can be obtained analogously employing the formula of the geometric series several times, and introducing the abbreviation ${\rm CV}^2_{q}={\rm var}_{x}\ q/\langle q\rangle_{x}^{2}$ with expected values according to the distribution p(x):

$$\begin{array}{rll} \sigma_{\rm On}^{2}(m,n) & = & c_{m}\, m\,(1-c_{m})\\ &&+ \ n\, c\,\big[(1-c)+c\,{\rm CV}_{q}^{2}\,(n-1)\big]\\ \sigma_{\rm Of\/f}^{2}(m,n) & = & (m+n)\, c\\ &&\times\big[(1-c)+c\,{\rm CV}_{q}^{2}\,(m+n-1)\big]\ . \end{array}$$

Note that CV _q →0 for f→0, and, in this limit, the variance formulas $\sigma_{\rm On}^{2}\to m\, c_{m}\,(1-c_{m})+n\, c\,(1-c)$, $\sigma_{\rm Of\/f}^{2}\to(m+n)\, c\,(1-c)$ from the present theory approximate those in Leibold and Kempter (2006).