Describing and deriving certain answers over partial databases

Abstract

Although there has been much work in recent years on answering queries using views, there has been less work on deriving answers from partial databases. That is given a partial database state D^V, materialized via the view V, what queries can be asked over D^V that can be answered with certainty using only the instance of the partial database and standard query evaluation mechanisms. We define these as the derivable answers and show several special cases in which we can compute and intensionally describe them.

1 Introduction

Under Reiter’s closed-world assumption (CWA) any formula that can not be proven from a given set of formulas, is considered to be false (Reiter 1978). As applied to databases this means that any fact not represented in a database state D is assumed to not hold in the world represented by D. In practice however, we often wish to invoke the CWA for portions of our databases. For example in a USA geography domain we may safely invoke CWA over the State relation, but we might not have not captured all tuples for the City relation. For example perhaps we only fully represent the large cities in our database.

Motro was one of the first to seriously look at this issue and he proposed a method in which an administrator declares completeness assertions to define portions of the database for which complete information has been supplied (Motro 1986, 1989, 1996). Using the example USA geography database depicted in Table 1, we may declare the completeness assertion {x|State(x)} to mean that we have data on all the states, and the more restrained completeness assertion that we have information on all the cities of size ‘large’, with $\{x |City(x) \wedge x.size = \textsf{`large'}\}$. Given such completeness assertions, Motro develops an approach to query answering that reports which answers to a given query are in fact complete in the real world. Thus if one was to pose a query for the “cities in Michigan”, Motro’s system would yield a complete extension for the cities in Michigan with size large and, to the point of this paper, be able to offer an exact intensional description of this query. Namely the user would be informed that their query was only complete for the large cities of Michigan.

Table 1 Part of an example USA geography database

It is worth reviewing the method that Motro uses to calculate such intensional descriptions. First off Motro limits attention to completeness descriptions of conjunctive queries (Chandra and Merlin 1977). His technique is to create special meta-tuples that represent these queries using an annotation scheme similar to query by example (QBE)(Zloof 1977). Thus for the example in Table 1 along with the completeness assertions considered thus far we see the creation of two meta relations depicted in Table 2. In Motro’s notation if an asterisk (*) prepends a value or variable or stands alone in a column, then the corresponding completeness assertion is projecting on the corresponding column.

Table 2 Representation of completeness assertions in meta-relations

Motro defines a set of transformations that mirror the query processing of conjunctive queries over the relations of the data oriented relations with the operations over the meta-tuples represented in meta-relations. The precise definitions of these operations are presented in Motro (1989) where definitions are provided for the relational algebra operations of projections, selection and Cartesian product. The result of these operations applied to our original query yield the completeness tuple depicted in Table 3, namely a tuple that represents the conjunctive query “all the large cities in Michigan”.

Table 3 Representation of meta answer to “Cities in Michigan”

Motro’s technique is limited to conjunctive queries and conjunctive completeness assertions. While many practical cases can be handled with conjunctive queries, one can envision cases where it would be very useful to include more expressive queries. For example suppose we issued the query for the states that do not have any large cities. This query should in fact be complete for the given database. That is if one was to evaluate such a query over the instance of the partial database, then exactly the states that do not have large cities would be in the result set. Similar examples may be constructed for superlative type queries such as “the smallest state with a large city.” Finally even queries using universal quantification (e.g. “business with stores in every large city of Michigan”) of queries employing double negation (e.g. “states that do not border states without a tall mountain”) could be considered. This paper extends Motro’s work to query languages containing such limited forms of negation.

There is a subtle derivability issue that emerges in Motro’s approach. To illustrate suppose that we had a completeness assertion for the city tuples for cities with a mayor who is a member of the democratic party, as depicted in Table 4. Thus what is shown in Table 4 is that while we project the city tuples we do not in fact have any information on tuples representing mayors. The issue then becomes, how do we handle a query such as “give the large cities with with democratic mayors”? While the database holds all such cities, the problem is that such a query applied to the actual database would yield the null result assuming that no other completeness assertion covered the table Mayor. The approach in this paper maintains derivability of answers over partial databases.

Table 4 Representation of completeness assertions

Motro’s technique is efficient, yet it is not proved to be complete. That is not all relevant covering views will necessarily be reported in the meta-answer. In subsequent work Halevy developed algorithms that were complete for exactly the problem of finding equivalent rewritings of conjunctive queries using sets of conjunctive views. Still the problem of finding complete maximally contained rewritings of conjunctive queries over conjunctive views remains unsolvable in the general case. The work here develops a case of expressive queries and view definitions which, given various testable condition, do in fact generate complete maximally contained rewritings.

1.1 A set theoretic treatment of querying partial databases

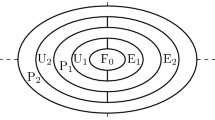
To orient the reader to the precise problem treated in this paper consider Fig. 1. We have W, the set of database tuples that represent the complete, through unavailable database state. The database state D is the state of our partial database. D is obtained by evaluating the view V over the complete database W. To keep everything based on sets of database tuples, V defines a filter that determines which tuples to let into D. It’s role is exactly that of completeness assertion is Motro’s work (Motro 1986, 1989, 1996) and the set of local completeness statements discussed in Halevy (1996).

Fig. 1

Set theoretic treatment of querying partial databases

Because V is simply a filter, $D \subseteq W$. Now given a user query Q, consider the evaluation of Q over the partial database D versus its evaluation over the complete database W. That is Q(D) versus Q(W). If we restrict our attention to filter queries that simply select for subsets of tuples in a database state, we obtain the set theoretic analysis of Fig. 1.

Figure 1 shows us that when we evaluate the filter query over the partial database state we may obtain incorrect answer tuples or correct answer tuples. In addition there may be missed answer tuples that we should have identified as answers and of course there are the unavailable answer tuples that D does not contain, but which could be intensionally described. To illustrate, consider the USA geography example above. If we query our partial database for “cities”, then all the large cities will be correct answer tuples and the non-large cities without democratic mayors will be unavailable answers tuples. Considering that we do not have any tuples in the relation Mayor, the query “cities with Republican mayors” will yield an empty result although there are many cities in D which do in fact have republican mayors. These are missed answer tuples. Finally if we evaluate the query “large cities without republican mayor” we will yield all of the cities in our database of which many will be incorrect answer tuples.

The contribution of the work here is to identify a testable condition, that, if met, will allow us to evaluate a query directly over the partial database and be guaranteed of yielding exactly the correct answer tuples, without generating any incorrect tuples and without missing any answer tuples. Moreover we will be able to calculate intensional descriptions of both the unavailable answer tuples as well as an intensional description of the correct answer tuples. The condition required to achieve this result are restrictive, though, we will show, general enough to cover many practical cases.

1.2 Organization of this article

Section 2 introduces the basic definitions of our system. The treatment is fairly standard, but the critical notion of typing tuples to relations as well as the notion of a filter query are introduced. These are non-standard assumptions, critical to what follows. Section 3 gives an abstract treatment of the problem of determining the exact portion of a query that can be derived over a partial database. Section 4 provides a special query language fragment based on the Shönfinkle-Bernays fragment (Bernays and Schönfinkel 1928) in which we may operationalize the concepts in Section 3. Section 5 presents another fragment based on the guarded fragment (Andreka et al. 1998; Grädel 1999) in which we may operationalize the concepts of Section 3. Section 6 discusses this work in relation to prior and contemporary work. Section 7 concludes.

2 Foundations

2.1 Basic notions

Let us assume the existence of three disjoint, countably infinite sets: att (attribute names), dom (universal domain of atomic values) and relname (relation names). Furthermore let us assume that dom is totally ordered and that we have a finite set of constant symbols C that uniquely identify elements in dom. Following the named perspective covered in Abiteboul et al. (1995), assume a function sort from relname to $\mathcal{P}^{\rm fin}$(att) (the family of finite subsets of att) which associates a finite set of attribute names with a given relation name. A relation schema is simply a relation name R interpreted under sort. We shall often write R[U] where U is a finite subset of attributes and sort(R) = U. A database schemaR, is a finite, non-empty set of relation names. Hereafter we shall assume the relational schema is fixed.

Tuples are viewed as functions. The tuple t over the relation schema R[U] is a total mapping from U to dom and is said to have the sort U. The value of t on the attribute A in U is denoted t(A). A relation state of a relation schema R[U] is a finite (possibly empty) set D _R of tuples with sort U. A database state of the database schema R is a mapping D with domain R, such that D(R) is a relation state D _R over R. We slightly abuse the notation and write t ∈ D to indicate that a tuple t is in the database state D. Furthermore for database states D and D′ we write $D \subseteq D'$ to state that all tuples in D are also in D′ and we use ∅ denote the empty state, i.e. the state with no tuples. Finally we denote the set of all possible database states as $\mathcal{U}$. Note that in this work we do not take database constraints into account.

2.1.1 Typed tuples

We stipulate that tuples are typed to one and only one relation schema. Formally there exists a function type from the tuples in D to R such that for the tuple t ∈ D, t ∈ D _R if and only if R = type(t). As a consequence it should be clear that each tuple in a database state belongs to one and only one relation state.

Given the typed nature of tuples we may speak of set operations on databases instances. So for $W \in \mathcal{U}$ and $W' \in \mathcal{U}$, W − W′ and W ∩ W′ are well defined.

2.2 Tuple relational calculus (Codd 1972)

Let tvar be an infinite set of tuple variables and assume z (and z′) is a tuple variable, A (A′) is an attribute in the sort of the relation that z (z′) ranges over and c₁,...,c _n are constants drawn from the finite set C. Furthermore assume that θ denotes one of the operators (=,>,<,≥,≤ or ≠). The following are atomic tuple formulas: R(z) (range conditions), z.Aθc _i (simple conditions), z.Aθz′.A′ (join conditions). All atomic formulas are tuple relational formulas and if F₁ and F₂ are tuple relational formulas, where F₁ has some free tuple variable z, then F₁ ∧ F₂, F₁ ∨ F₂, $\neg F_{1}$, $(\exists z)F_{1}$ and ( ∀ z)F₁ are also tuple relational formulas. Without loss of generality, assume that all variables within a formula are distinct and the function var applied to a formula F returns all of its variables. Finally the substitution {z ↦z′} applied to F replaces all occurrences of the variable z with the variable z′ throughout F. We refer the reader to Ullman (1989) for the semantics of tuple calculus. Needless to say it corresponds directly to standard first order logic.

2.3 Filter queries

We shall limit our attention to a simple type of query that returns whole tuples of schema relations. These queries can be seen as filters that decide for each tuple in a database instance whether that tuple is to be included in the answer set.

Definition 1

(filter queries) A filter query is an expression of the form {x|γ(x)}, where γ(x) is a tuple relational formula over the free tuple variable x.

If the query Q is {x ∣ γ(x)} then we denote its application to the database state W as Q(W) or, more formally {x ∣ γ(x)}(W). For every tuple t, t ∈ {x ∣ γ(x)}(W) if and only if t ∈ W and {x ↦t}γ(x) is true in W. Hereafter in this paper, assume all references to queries are references to filter queries.

Definition 2

(Query containment and equivalence) Query Q contains query Q′, denoted $Q' \sqsubseteq Q$ if for all databases $W \in \mathcal{U}$, $Q'(W) \subseteq Q(W)$. Query Q is equivalent to query Q′, denoted Q′ ≡ Q when $Q' \sqsubseteq Q$ and $Q \sqsubseteq Q'$

3 Certain and derivable queries over partial databases

Assume two database states over the same schema R: the state W of the complete database that describes the real world, and the state D of a partial database. The partial database state D contains the image of the view mappingV over W where V is a filter query that specifies which tuples in W to let into D. Thus by necessity $D \subseteq W$. As a point of notation, the database state D^V indicates that the view mapping V was used to build it.

Definition 3

(A view mapping V) A view mapping V is a query {x ∣ v(x)} that when applied to the real world database state W gives us the state D^V of our partial database. That is D^V = V(W).

These view mappings serve the same role as completeness assertions in Motro’s work.

Definition 4

(A certain answer to Q over D^V) Let Q be a query, V be a view mapping and D^V a partial database. A tuple τ is a certain answer to Q over D^V if for all database states $W \in \mathcal{U}$, if D^V = V(W) then τ ∈ Q(W).

This notion of certain answer here is equivalent to the standard definition of certain answer over views under the closed world assumption (see for example Halevy 2000; Abiteboul and Duschka 1998).

Definition 5

(A derivable answer to Q over D^V) Let Q be a query, V be a view mapping and D^V a partial database. A tuple τ is a derivable answer to Q over D^V if for all database states $W \in \mathcal{U}$, if D^V = V(W) then τ ∈ Q(W) and τ ∈ Q(D^V).

The definition of derivable answer extends certain answer with the added condition that the answer must be derivable from the partial database itself using standard query evaluation.

The following two definitions extend the definitions of certain and derivable answers, to certain and derivable queries. That is queries that return exclusively certain (or derivable) answers.

Definition 6

(A certain query Q over D^V) Let Q be a query, V be a view mapping and D^V a partial database. Q is a certain query over D^V if for all $W \in \mathcal{U}, W' \in \mathcal{U}$, if D^V = V(W) = V(W′) then Q(W) = Q(W′). We denote this by $\textsf{certain}(Q,D^V)$.

Definition 7

(A derivable query Q over D^V) Let Q be a query, V be a view mapping and D^V a partial database. Q is a derivable query over D^V if for all $W \in \mathcal{U}, W' \in \mathcal{U}$, if D^V = V(W) = V(W′) then Q(W) = Q(W′) = Q(D^V). We denote this by $\textsf{derivable}(Q,D^V)$.

Example 1

Consider a relation schema R with the relations R(A,B), S(C,D) and T(E) and the database state W with exactly relation states W _R  = {(1,0),(1,1),(0,1)}, W _S  = {(1,0),(1,1)} and W _T  = {(1)}. Let the view mapping $V = \{x \vert (R(x) \wedge (\exists y) (S(y) \wedge x.A=y.C \wedge x.B = y.D)) \vee T(x)\}$. If D^V = V(W) then $D^{V}_R = \{(1,0),(1,1)\}$, $D^{V}_S = \{\}$ and $D^{V}_T = \{(1)\}$. It should be clear that (1) is a certain and derivable answer to {x ∣ T(x)} and (1,1) is a certain, but not derivable, answer to {x ∣ S(x)}. Also $\textsf{derivable}(\{x \vert T(x)\},D^V)$, $\textsf{certain}(\{x \vert R(x) \wedge (\exists y) (S(y) \wedge x.B=y.C)\},D^V)\}$, but not $\textsf{derivable}(\{x \vert R(x) \wedge (\exists y) (S(y) \wedge x.B=y.C)\},D^V)\}$.

Given a user’s arbitrary query, we are interested in determining the largest query that will return only the derivable answers over the partial database state. That is we are interested in identifying exactly the query that covers the correct answer tuples in Fig. 1. This corresponds directly with the maximally contained derivable writing of Q over D^V.

Definition 8

(Maximally contained derivable rewriting of Q over D^V) Let Q be a query, V be a view mapping and D^V a partial database. Q′ is the maximally contained derivable rewriting of Q over D^V if $Q' \sqsubseteq Q$ and $\textsf{derivable}(Q',D^V)$ and there does not exist any Q′′ where $Q' \sqsubseteq Q'' \sqsubseteq Q$ and $\textsf{derivable}(Q'',D^V)$. We denote this such a query with $\textsf{max-der}(Q,D^V)$.

Since the maximally contained derivable writing is an abstraction, we must characterize computed rewritings with respect to the exact maximally contained rewriting.

Definition 9

(A sound derivable rewriting of Q using D^V) Let Q be a query, V be a view mapping, D^V a partial database and $\textsf{rewrite}(Q,D^V)$ be a rewriting of Q using V and D^V. $\textsf{rewrite}(Q,D^V)$ is a sound derivable rewriting Q over D^V if $\textsf{rewrite}(Q,D^V) \sqsubseteq \textsf{max-der}(Q,D^V)$

A sound rewriting excludes the incorrect answer tuples of Fig. 1.

Definition 10

(A complete derivable rewriting of Q using D^V) Let Q be a query, V be a view mapping, D^V a partial database and $\textsf{rewrite}(Q,D^V)$ be a rewriting of Q using V and D^V. $\textsf{rewrite}(Q,D^V)$ is a complete derivable rewriting Q over D^V if $\textsf{max-der}(Q,D^V) \sqsubseteq \textsf{rewrite}(Q,D^V)$

A complete rewriting excludes the missing answer tuples of Fig. 1.

The following relationship emerges directly from the set theoretic treatment of Fig. 1. As we shall see in the subsequent sections the given test can be operationalized under various assumption about the language in which we express queries and views.

Theorem 1

(The completeness test) If rewrite(Q,D^V) is a sound derivable rewriting of Q over D^V , then if for all $W \in \mathcal{U}$ , (V(W) − rewrite(Q,D^V)(W)) ∩ Q(W) = ∅ then rewrite(Q,D^V) is a complete derivable rewriting of Q over D^V

Proof

Assume that rewrite(Q,D^V) is a sound derivable rewriting of Q over D^V and that for all $W \in \mathcal{U}$, (V(W) − rewrite(Q,D^V)(W)) ∩ Q(W) = ∅. Now suppose rewrite(Q,D^V) is not a complete derivable rewriting of Q over D^V. This would mean that for at least one $W' \in \mathcal{U}$ where D^V = V(W′) there is a tuple τ where $\tau \in \textsf{max-der}(Q,D^V)(W')$ and $\tau \notin \textsf{rewrite}(Q,D^V)(W')$. If $\tau \in \textsf{max-der}(Q,D^V)(W')$ then τ is a derivable answer to Q over D^V and thus τ ∈ D^V and, by consequence, τ ∈ V(W′). Thus (V(W′) − rewrite(Q,V)(W′)) must be non-empty with τ as a member. But based on the assumption that for all $W \in \mathcal{U}$ (including W′), that (V(W) − rewrite(Q,V)(W)) ∩ Q(W) = ∅ then τ ∉ Q(W′) which is a contradiction of $\tau \in \textsf{max-der}(Q,D^V)(W')$. Hence, by contradiction, rewrite(Q,D^V) is a complete derivable rewriting of Q over D^V. □

4 Filter queries of the Shönfinkle-Bernays fragment (Bernays and Shönfinkle 1928; Börger et al. 1997)

We now explore a case in which we are able to operationalize the test within Theorem 1.

4.1 The language $\mathcal{L}_{SB}$

Let us introduce some notions that will help us to define a special language $\mathcal{L}_{SB}$. A positive query component built over the free tuple variable x is a formula of the form $(\exists y_{1})(\exists y_{2})...(\exists y_{n}) \rho(y_1,...,y_n)\wedge \varphi (x,y_1,...,y_n)$, where ρ is a conjunction of range conditions $R_{a_1}(y_1) \wedge ... \wedge R_{a_n}(y_n)$ and ϕ is a well formed Boolean formula of simple and join conditions over the tuple variables x,y₁,..,y _n . By defining positive query components in such a way, we guarantee their safety.

A signed query component is either a positive query component or the negation of a positive query component. Let us refer to a signed query component as a component and, when necessary, let us use the terms positive or negative component to indicate sign.

Definition 11

(The language $\mathcal{L}_{SB}$) The language $\mathcal{L}_{SB}$ consists of all formulas of the form:

$$ R(x) \wedge \alpha(x) \wedge \psi_{1}(x) \wedge ... \wedge \psi_{n}(x) $$

where R(x) restricts x to range over an arbitrary relation R, α(x) is a Boolean formula of simple conditions over x and ψ _i is a signed query component over x. We state that that the type of such a formula is R.

The language $\mathcal{L}_{SB}^{pos}$ is a sub-language of $\mathcal{L}_{SB}$ that uses only positive query components.

Lemma 1

($\mathcal{L}_{SB}$ is decidable for emptiness) For $l(x) \in \mathcal{L}_{SB}$ we may decide if {x ∣ l(x)}(W) = ∅ for all $W \in \mathcal{U}$.

Proof

To determine if {x ∣ l(x)} is necessarily empty, we determine if the sentence $\mathsf{encode}((\exists x)(l(x)))$ is unsatisfiable. The function encode yields a first order sentence that expands the supplied tuple calculus formula and, in addition, expresses the unique names assumption (UNA) and LessThan for the constants used in l(x). The sentence $\mathsf{encode}((\exists x)(l(x)))$ where $l(x) \in \mathcal{L}_{SB}$ is always within the well known decidable Shönfinkel1-Bernays class (Bernays and Schönfinkel 1928; Börger et al. 1997) with equality. That is the resulting formula has the quantifier prefix $\exists^{*}\forall^{*}$. □

4.2 The language $\mathcal{Q}_{SB}$

We define the language $\mathcal{Q}_{SB}$ as the closure of $\mathcal{L}_{SB}$ over disjunction.

Definition 12

(The language $\mathcal{Q}_{SB}$) $q(x) \in \mathcal{Q}_{SB}$ if q(x) is written as a finite expression l₁(x) ∨ ... ∨ l _k (x) where $l_{i}(x) \in \mathcal{L}_{SB}$

The language $\mathcal{Q}_{SB}^{pos}$ is a sub-language of $\mathcal{Q}_{SB}$ in which all disjuncts are in $\mathcal{L}_{SB}^{pos}$.

Lemma 2

($\mathcal{Q}_{SB}$ is decidable for emptiness) Given $q(x) \in \mathcal{Q}_{SB}$ we may decide if {x ∣ q(x)}(W) = ∅ for all $W \in \mathcal{U}$.

Proof

An emptiness test may be conducted for each disjunct of q(x). Since the number of disjuncts is finite, this process will terminate with an answer. □

Lemma 3

(Syntactic difference of $\mathcal{Q}_{SB}$ queries) Let $q_{1}(x) \in \mathcal{Q}_{SB}$ and $q_{2}(x) \in \mathcal{Q}_{SB}$ . There is a $q_{3}(x) \in \mathcal{Q}_{SB}$ such that for all $W \in \mathcal{U}$ , {x ∣ q₃}(W) = {x ∣ q₁}(W) − {x ∣ q₂}(W).

Proof

A simple consequence of DeMorgan’s law, associativity and distributivity of ∧ over ∨. □

Observe that using DeMorgan’s law we may in fact calculate q₃(x) given q₁(x) and q₂(x). The typing of tuples (see Section 2.1.1) is critical for this result.

Example 2

Under the normal non-typed case, given the database relations R[AB] and S[AB], the query $\{x \vert R(x)\} - \{x \vert S(x)\} = \{x \vert R(x)\wedge \neg S(x)\}$. In the typed case however, $\{x \vert R(x)\wedge \neg S(x)\}$ = {x ∣ R(x)}. Thus in the traditional, non-typed case, a calculation of difference would need to be performed over the states of the given relations R and S. In contrast in the typed case the calculation can be made purely at the intensional level.

Lemma 4

(Syntactic intersection of $\mathcal{Q}_{SB}$ queries) Let $q_{1} \in \mathcal{Q}_{SB}$ and $q_{2} \in \mathcal{Q}_{SB}$ . Then there is a $q_{3} \in \mathcal{Q}_{SB}$ such that for all database states {x ∣ q₁} ∩ {x ∣ q₂} = {x ∣ q₃}.

Proof of Lemma 4

A consequence of Lemma 3. □

Again observe that we may actually calculate q₃ given q₁ and q₂.

Theorem 2

(Containment and equivalence over $\mathcal{Q}_{SB}$) If $q_{1}(x) \in \mathcal{Q}_{SB}$ , $q_{2}(x) \in \mathcal{Q}_{SB}$ , then one may decide if:

• 1. for all $W \in \mathcal{U}$ , $\{x \vert q_{1}(x)\}(W) \subseteq \{x \vert q_{2}(x)\}(W)$

• 2. for all $W \in \mathcal{U}$, {x ∣ q₁(x)}(W) = {x ∣ q₂(x)}(W)

Proof

Property 1 is true iff for all $W \in \mathcal{U}$, {x ∣ q₁(x)}(W) − {x ∣ q₂(x)}(W) = ∅. This may be decided based on Lemmas 3 and 4. The decidability of Property 2 follows directly from the ability to decide Property 1. □

4.3 Restricting view mappings to $\mathcal{Q}_{SB}^{pos}$ and queries to $\mathcal{L}_{SB}$

We now turn to a restricted version of the problem developed in Section 3. Our restriction is that the query Q = {x ∣ l(x)} where $l(x) \in \mathcal{L}_{SB}$ and the view mapping V = {x ∣ v(x)} where $v(x) \in \mathcal{Q}_{SB}^{pos}$.

Definition 13

(A rewrite step) Given a query Q = {x ∣ l(x)} where $l(x) \in \mathcal{L}_{SB}$ and V = {x ∣ l₁(x) ∨ ... ∨ l _n (x)} with each $l_i(x)\in \mathcal{L}^{pos}_{SB}$, and a non-empty set Ω of non-rooted variables in Q, a rewrite step is the query obtained by matching of z ∈ Ω with the i-th disjunct of V, rewriting Q into Q′ = {x ∣ l′(x)} according to the following cases:

• 1. If the x in l _i (x) ranges over a different relation than z in l(x), then the rewriting has failed.

• 2. If z = x of l(x) then l′(x) = l(x) ∧ l _i (x).

• 3. If l _i (x) and z is within the j-th signed component of l(x) where $\psi_j(x)\, =\, s\, \cdot ( \exists y_1 )\,...\,( \exists z )\,...\,( \exists y_m ) \rho ( y_1,, z,,y_m ) \wedge \varphi(x, y_1,...,z,...,y_m)$ and ς(z) = l _i (x), then $l'(x) = R(x) \wedge \alpha(x) \wedge \psi_{1}(x) \wedge ... \wedge \psi_{j-1}(x) \wedge \psi_{j+1}(x) \wedge ... \wedge \psi_{n}(x) \wedge s \cdot (\exists y_1)...(\exists z)...(\exists y_m) (\rho( y_1,...,z,...,y_m) \wedge \varphi(x, y_1,...,z,...,y_m)\wedge \{x \mapsto z\} l_i(x))$.

A final check is made to verify that $Q' \sqsubseteq Q$ and z is marked as a rooted variable in Q′.

Each successful rewrite step in a rewrite marks a variable as rooted and inserts a disjunct from the view mapping into the query. A sequence of rewrite steps $\langle Q_1,\Omega_1 \rangle \rightarrow ... \rightarrow \langle Q_m, \emptyset \rangle$ where Ω₁ is the set of all variables in Q₁ marked as non-rooted. Q _m is a query expression with all rooted variables is a rooted rewrite derivation. Since each rewrite step may introduce new non-rooted variables from the view mapping, the rewrite process does not necessarily terminate. Still in those cases where it does terminate, the set of all the final queries in rooted rewrite derivations is the set of rooted rewrites. It should be clear that all rooted rewrites can be expressed are within $\mathcal{L}_{SB}$ and the disjunction of all such rooted rewrites is an expression with in $\mathcal{Q}_{SB}$. We term this disjunction all finite rooted rewrites as rewrite(l(x),v(x)).

Theorem 3

(soundness of rewriting) Given $l(x) \in \mathcal{L}_{SB}$ over $v(x) \in \mathcal{Q}_{SB}^{pos})$ , rewrite(l(x),v(x)) is a sound derivable rewriting)

Proof

Assume that τ ∈ {x ∣ rewrite(l(x),v(x))}(D^V) but there exists a $W \in \mathcal{U}$ where D^V = V(W) and τ ∉ {x ∣ rewrite(l(x),v(x))}(W). In the case that $\mathsf{rewrite}(l(x),v(x)) \in \mathcal{Q}_{SB}^{pos}$ this is a contradiction based on monotonicity. That is since $D^V \subseteq W$ and since rewrite(l(x),v(x)) is based solely on the view mapping and thus uses only tuples within D^V to decide whether τ is an answer, then τ ∈ {x ∣ rewrite(l(x),v(x))}(W). In the case that there is a disjunct l′(x) in rewrite(l(x),v(x)) which contains a negative component, there must be a τ′ ∈ W (τ′ ∉ D^V) which makes the overall negative component false when evaluated over W (as opposed to true when evaluated over D^V). But since all variables in l′(x) are based solely on the view mapping there can be no τ′ ∉ D^V that serves as a spoiler to negate the negative component. Thus for all τ ∈ {x ∣ rewrite(l(x),v(x))}(D^V) τ is a derivable answer and thus {x ∣ rewrite(l(x),v(x))} is a sound derivable rewriting. □

Example 3

Let us consider the first example posed in the introduction. We have the following completeness statement

$$\begin{array}{rll} V &=& \{x \vert \\ &&\; {\kern3pt}State(x) \\ &\bigvee & City(x) \wedge x.size = \textsf{`large'}\} \\ \end{array}$$

When $Q = \{x \vert City(x) \wedge (\exists y)(State(x) \wedge x.state = y.name \wedge x.name = \textsf{`Michigan'})\}$, the sound re-writing of Q over V takes two steps and is just $Q' = \{x \vert City(x) \wedge x.size=\textsf{`large'} \wedge (\exists y)(State(x) \wedge x.state = y.name \wedge x.name = \textsf{`Michigan'})\}$. Via a theorem prover we can establish that the completeness test is passed and thus Q′ may be applied to the partial database state and return all certain answers.

When $Q = \{x \vert State(x) \wedge \neg (\exists y)(City(y) \wedge x.name = y.state \wedge y.size=\textsf{`large'})\}$, an equivalent rewriting is achieved via two rewrite steps and the completeness test is passed.

When $Q = \{x \vert State(x) \wedge (\exists y)(City(y) \wedge x.name = y.state \wedge y.size=\textsf{`large'}) \wedge \neg (\exists y)(\exists z)(State(y) \wedge y.population \leq x.population \wedge City(z) \wedge y.name\! = z.state \wedge z.$ $size=\textsf{`large')} \}$, an equivalent rewriting is achieved via four rewrite steps and the completeness test is passed. Note had the query been for the smallest state with a city, then the rewriting would have failed.

Example 4

In the extended example in the introduction. We have the following completeness statement:

$$\begin{array}{rll}V &=& \{x \vert \\ &&\; {\kern7pt}State(x) \\ &\bigvee & City(x) \wedge x.size = \textsf{`large'}\\ &\bigvee & City(x) \wedge (\exists y)(Mayor(y) \wedge x.name=y.city \wedge y.party = \textsf{`democratic'})\} \\ \end{array}$$

In this case only the last two queries in the above example succeed in achieving a rewriting. The reason the first query fails is that the variable for Mayor remains un-rooted in all cases. Thus even though there are rooted rewrites of the input query, none are broad enough to pass the completeness test.

5 Filter queries of the guarded fragment (Andreka et al. 1998; Grädel 1999)

In an analogous manner to Section 4, here we shall develop an alternative query language in which we can operationalize the concepts of Section 3. This language is based directly on the guarded fragment of first-order logic (Andreka et al. 1998; Grädel 1999). This language permits a much more expressive use of negation than $\mathcal{L}_{SB}$. We call this new language $\mathcal{L}_{G}$ and present its definition here.

We inductively define the set of guarded components. In this definition, we assume that the guarded component ψ(y) over the variable y may be written as $s \cdot (\exists y) (P(y) \wedge \phi(y))$ where s is the sign (empty or $\neg$), P(y) is the guard and φ(y) is the body of the guarded component.

Definition 14

(Guarded components)

• 1. The formula $(\exists y) (P(y) \wedge \phi(y))$ is a guarded component where ϕ(y) is a conjunction of meaningful set and simple conditions limited to the operators = and ≠ over y.

• 2. If ψ and ψ′ are guarded components ($\psi \equiv s \cdot (\exists y) (P(y) \wedge \phi(y))$ and $\psi' equiv s' \cdot (\exists y') (P'(y') \wedge \phi'(y'))$), then $(\exists y) (P(y) \wedge \phi(y) \wedge s' \cdot (\exists y') (P'(y') \wedge y.a = y'.b \wedge \phi'(y')))$ is a guarded component where y.a = y′.b is a meaningful equality join between the attribute a of P and the attribute b of P′.

• 3. If ψ and φ are guarded components, then ψ ∧ φ and $\neg \psi$ are guarded components.

Definition 15

(The language $\mathcal{L}_{G}$) The language $\mathcal{L}_{G}$ consists of all formulas of the form,

$$ P(x) \wedge \left(\bigwedge\limits_{i=1}^{n} \phi_i(x)\right) $$

where P is an arbitrary relation and ϕ _i is either a Boolean formula of simple and set conditions over x or a guarded component over x.

A simple translation of $\mathcal{L}_{G}$ to the domain calculus results in a formula in the guarded fragment (Andreka et al. 1998; Grädel 1999), a decidable fragment of first order logic. Thus we can decide query emptiness of $\mathcal{L}_{G}$ based queries. Moreover we can close $\mathcal{L}_{G}$ under disjunction and define $\mathcal{Q}_{G}$. The resulting language is decidable for emptiness (analogous to Lemma 2 above) and the syntactic query difference and intersection properties hold over $\mathcal{Q}_{G}$. Results analogous to Theorem 2 and Theorem 3 above hold for $\mathcal{Q}_{G}$. In fact because $\mathcal{L}_{G}$ allows for alternation, we may broaden its applicability to Q = {x ∣ l(x)} where $l(x) \in \mathcal{L}_{G}$ and the view mapping V = {x ∣ v(x)} where $v(x) \in \mathcal{Q}_{G}$.

Example 5

Consider the following completeness statement

$$\begin{array}{rll} V &=& \{x \vert \\ &&\; {\kern4pt}State(x) \\ &\bigvee & City(x) \wedge x.size = \textsf{`large'} \\ & \bigvee & Borders(x)\} \\ \end{array}$$

Where Borders(state1,state2) is a relation that specifies which states border each other. When we search for “states that do not border states that do not have large cities” we have the formal query $Q = \{x \vert State(x) \wedge \neg (\exists y)(Borders(y) \wedge x.name = y.state1 \wedge \neg (\exists z)(City|(z) \wedge y.state2 = z.state \wedge x.size = \textsf{`Large'}))\}$. This query is within $\mathcal{L}_{G}$ and after three rewrite steps an equivalent rewriting is achieved.

6 Discussion

There has been much past work that has looked at rewriting queries over views (see Halevy 2000, 2001, for a systems and theory survey). There are two related problems. The first is that of finding an equivalent rewriting of a query over a set of views, and the second is that of finding a maximally contained rewriting of a query over a set of views. The later problem is of interest here—we assume that user queries may be broader than what the view mapping offers. Typically approaches to obtaining maximally contained rewritings are based on rewriting the query solely in terms of the set of views, replacing each predicate in a query with a view definition. When a rewritten query is evaluated it is done so based on the extensions of these views. While this technique can be made to work in the standard relational environment, it does require some extra processing steps and storage of view extensions in separate tables. Such rewriting techniques have been applied to conjunctive queries and sets of conjunctive query view definitions.

The process of finding maximally contained rewritings is inherently combinatorial, typically bounded by the number of conjunctive views raised to the power of the query length. While this may seem impractical, one must keep in mind that the size of the query is the critical parameter and typically queries do not involve more than several relations. The combinatorial cost in the work presented here is further increased by the fact that views must in turn be rewritten by other views to root all variables. In certain cases this may lead to non-terminating rewrites. Simple non-cyclicity conditions can be placed on view mappings to guarantee termination, but even so the worst case complexity is rather dire. In essence we simply accept this and just attempt to find a rewriting that passes the completeness test of Theorem 1. In cases where a rewriting can not be found we don’t make any claims of completeness.

Generally speaking rewriting approaches have great difficulty with negation in either the query or the view definitions. A straight forward rewriting of a query using negation is likely to generalize a query and thus such approaches require some type of theorem prover to guarantee that a rewriting is contained by the original query. The work here is the only case the author is aware of that directly explores negation in queries rewritten over views. This is achievable here because of the strict conditions placed on the query and view definitions—namely that they are filter queries fitting into the fragments defined in either Section 3 or 4.

Although this paper introduces the term derivable answers (i.e. answers that are certain and can be derived directly from a partial database), in essence the problem was looked at in Larson and Yang (1985) as the problem of answering queries over materialized views using relational algebra over the materialized relations. Only the base case of a single conjunctive query over a single conjunctive view mapping was considered and the line of research was largely abandoned. The problem of deciding certain answers over materialized views was addressed in Abiteboul and Duschka (1998). That work encoded the completeness constraints using conditional tables (Imieliński and Lipski 1981). Each tuple in the materialized view was decided using a deduction method, of combinatorial cost in the data size of the materialized view. This work is one of the few other places in the literature in which negation in view mappings and queries is considered. Still the query mechanism is exotic and is based on a tuple-by-tuple analysis. Furthermore there is no attempt to intensionally describe certain (or unavailable) answers.

A primary advantage of the approach here is that the resulting rewriting of a query, if it passes the completeness test, can be applied directly over a given partial database using off-the-shelf relational engines and derive exactly the correct answers to the to the original query. The completeness test may be decided using a high performance theorem prover (e.g. (Weidenbach et al. 2002) in the case of the Shönfinkle-Bernays fragment and other theorem proving mechanisms in he case of the guarded fragment (Ganzinger and de Nivelle 1999)).

The limitation of the queries and view mappings here to only be filter queries is a serious limitation. Still when one considers schema such as triple stores stored as property tables (that is the verb value names a table in which the subject value and object value are stored as arguments) then it is quite conceivable that projection is not exercised and filter queries are sufficient. In other cases one may envision an approach where schemata are losslessly decomposed into a dependency preserving sub-schema over which filter queries may capture the important projection patterns over the original schema. The theory for performing such decompositions is very well understood.

A partial implementation of the concepts described in this article has been carried out for the C-Phrase natural language system for databases (Minock 2007). Of particular interest a paraphrasing mechanism has been built to describe queries of $\mathcal{L}_{SB}$ (Minock 2006). This is critical to communicate the intensional descriptions of completeness (or incompleteness) to users. We envision a system in which administrators (or even users) are able to declare in natural language completeness statements over their databases. Such descriptions accumulate a view mapping and then user queries can be characterized in terms of their completeness.

7 Conclusions

Aside from Motro’s initial work in the area, there has been very little attention paid to generating intensional descriptions that characterize either the portion of a query that can be answered with certainty over a partial database or the portion of a query that is inaccessible over the partial database given the view mapping. This paper reopens that issue, using query rewriting and theorem proving to derive exact descriptions of what portion of a user’s query can be answered correctly over a partial database. Moreover the evaluation of this intensional description over the partial database yields correct answers. The results are achieved by limiting user queries and completeness assertion to certain classes of filter queries. The two classes considered in this paper are $\mathcal{L}_{SB}$ and $\mathcal{L}_{G}$, both capable of expressing limited forms of negation.