Repertoire Contraction

Abstract

The basic assumption of repertoire contraction is that only some of the logically closed subsets of the original belief set are viable as contraction outcomes. Contraction takes the form of choosing directly among these viable outcomes, rather than among cognitively more far-fetched objects such as possible worlds or maximal consistent subsets of the original belief set. In this first investigation of repertoire contraction, postulates for various variants of the operation are introduced. Necessary and sufficient conditions are given for when repertoire contraction coincides with AGM contraction or with operations generated by AGM-style contraction on a belief base. A close connection is shown to hold between repertoire contraction and specified meet contraction.

Appendix: Proofs

Lemma 1

If compactness and Zorn’s lemma hold, then: If $X \subseteq A$ and $X \nvdash p$, then there is some $X^{\prime }$ such that $X \subseteq X^{\prime } \in A \perp p$. (upper bound property)

Proof of Lemma 1

See (Alchourrón and Makinson (1981), p. 129).

Lemma 2

$\mathrm{Cn}(\{a \vee b\}) = \mathrm{Cn}(\{a\}) \cap \mathrm{Cn}(\{b\})$

Proof of Lemma 2

See (Hansson (1999), p. 28).

Lemma 3

Let $K$ be logically closed, $X \in K \perp p$, and $q \in K \setminus X$. Then $X \in K \perp q$.

Proof of Lemma 3

See Alchourrón et al. (1985) or (Hansson (1999), p. 48).

Lemma 4

Let $A$ be a finite set of sentences. Then the following two conditions on a set $X$ of sentences are equivalent:

• 1 There is some $p$ such that $X \in A \perp p$.

• 2 There is some $p$ such that $\{X\} = A \perp p$.

Proof of Lemma 4

Hansson (1995) or (Hansson (1999), p. 60).

Lemma 5

The following three conditions are equivalent:

• 1. $A\perp p=A \perp q$

• 2. $A\bot \!\!\!\bot p=A\bot \!\!\!\bot q$

• 3. For all subsets $X$ of $A$: $X\vdash p$ iff $X\vdash q.$

Proof of Lemma 5

Hansson (1994) or (Hansson (1999), pp. 170–171).

Lemma 6

$\bigcap (A\perp p) =A \setminus \left(\bigcup (A \bot \!\!\!\bot p)\right)=\{q \in A\mid$ For all $X\subseteq A: X \vdash p$ iff $X\cup \{q\}\vdash p\}.$

Proof of Lemma 6

Hansson (1994) or (Hansson (1999), p. 171).

Lemma 7

Let $K$ be a belief set and let $p \in K$. Then (1) $K \sim p = K \cap \mathrm{Cn}(\{ \lnot p\})$, and (2) if $K$ is finite-based, then $K \sim p = \mathrm{Cn}(\{{ \& }K \vee \lnot p\})$.

Proof of Lemma 7

For (1), see Alchourrón and Makinson (1982) or (Hansson (1999), pp. 125–126). (2) follows from (1) and Lemma 2.

Lemma 8

Let $A$ and $B$ be sets of sentences and $p$ a sentence such that $\{A\} = B \perp p$. Let $\sigma$ be an incision function on $B$. Then $B \approx _\sigma p = A$.

Proof of Lemma 8

Let $q \in B \setminus A$. Then $q$ is not an element of any element of $B \perp p$, and it follows from Lemma 1 that $q \vdash p$ and $\{q\} \in B \bot \!\!\!\bot p$. Since $A \nvdash p$, no subset of $A$ is an element of $B \bot \!\!\!\bot p$. Furthermore, since each set containing elements from both $A$ and $B \setminus A$ has a proper subset that is an element of $B \bot \!\!\!\bot p$, no such set can itself be an element of $B \bot \!\!\!\bot p$. Hence $B \bot \!\!\!\bot p = \{\{q\} \mid q \in B \setminus A \}$, and when applied to $B \bot \!\!\!\bot p$ any incision function $\sigma$ will remove exactly the elements of $B \setminus A$, thus $B \approx _\sigma p = A$.

Proof of Theorem 1,

  Part I:

Recovery $\Rightarrow$ Relevance: Let $z \in K \setminus (K \div p)$. Then due to Vacuity, $p \in K$. Using Closure and Lemma 1, let $K \div p \subseteq X \in K \perp z$. Due to Recovery, $K \div p \vdash p \rightarrow z$, hence $X \vdash p \rightarrow z$. Since $X \nvdash z$ it follows that $X \nvdash p$. Due to Lemma 3, since $p \in K$ we also have $X \cup \{z\} \vdash p$.

Relevance $\Rightarrow$ Core-retainment: Directly from the definitions.

Core-retainment $\Rightarrow$ Recovery: Suppose that Core-retainment holds but Recovery does not hold. Then there are $p, q \in K$ such that $q \notin \mathrm{Cn}((K \div p) \cup \{p\})$. It follows that $p\rightarrow q \in K \setminus K\div p$. Due to Core-retainment there is some $X \subseteq K$ such that $X \cup \{p \rightarrow q\} \vdash p$ but $X \nvdash p$. This is impossible since $X \cup \{p \rightarrow q\} \vdash p$ implies $X \vdash p$. We can conclude from this contradiction that Recovery holds.

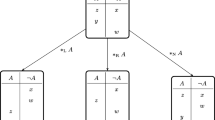
Part II, Positive Results: We are going to show that the five implications indicated in the figure hold:

Recovery $\Rightarrow$ Preservativity: Let $K^{\prime } \nsubseteq K \div p$. Let

$K^{\prime \prime } = K\div (({ \& }(K \div p) \ \& \ ({ \& }K^{\prime } \rightarrow p)) \rightarrow { \& }K)$.

We are going to show (a) that $({ \& }(K \div p) \ \& \ ({ \& }K^{\prime } \rightarrow p)) \rightarrow { \& }K$ is not a tautology, (b) that $K \div p \subseteq K^{\prime \prime }$, (c) that $K^{\prime \prime } \nvdash p$, and (d) that $K^{\prime \prime } \cup K^{\prime } \vdash p$.

• (a): Suppose that the contrary is true. We then have: $\vdash ({ \& }(K \div p) \ \& \ ({ \& }K^{\prime } \rightarrow p)) \rightarrow { \& }K$ $\vdash ({ \& }(K \div p) \ \& \ ({ \& }K^{\prime } \rightarrow p)) \rightarrow { \& }K^{\prime }$ (Since $K^{\prime } \subseteq K$) $\vdash { \& }(K \div p) \rightarrow { \& }K^{\prime }$ (Truthfunctionally) contrary to $K^{\prime } \nsubseteq K \div p$.

• (b): We have: $K^{\prime \prime } \vdash (({ \& }(K \div p) \ \& \ ({ \& }K^{\prime } \rightarrow p)) \rightarrow { \& }K) \rightarrow { \& }K$ (Recovery) $K^{\prime \prime } \vdash { \& }(K \div p) \ \& \ ({ \& }K^{\prime } \rightarrow p)$ (Truthfunctionally since ${ \& }K \vdash ({ \& }(K \div p) \ \& \ ({ \& }K^{\prime } \rightarrow p)$)). $K \div p \subseteq K^{\prime \prime }$ (Closure)

• (c): We have: $K \div p \subseteq K^{\prime \prime }$ (Part b) $K^{\prime \prime } \vdash p \rightarrow { \& }K$ (Since $K \div p \vdash p \rightarrow { \& }K$ due to Recovery.) $K^{\prime \prime } \nvdash p$ (Part (a) and Success)

• (d): Directly from $K^{\prime \prime } \vdash { \& }K^{\prime } \rightarrow p$ that was shown in (b).

Preservativity $\Rightarrow$ Weak Preservativity: Directly from the definitions.

Recovery $\Rightarrow$ Defeasible Maximality: Let Recovery hold and let $K \div p \subset K^{\prime } \nvdash p$. We need to find some $K^{\prime \prime }$ such that $K \div p \subset K^{\prime \prime } \nvdash p$ and $K^{\prime } \cup K^{\prime \prime } \vdash p$. Let $X = \mathrm{Cn}((K \div p) \cup \{ { \& }K^{\prime } \rightarrow p\})$. Using Finite-based Outcome, let $K^{\prime \prime } = K \div ({ \& }X \rightarrow { \& }K)$.

First suppose that $X \vdash p$, i.e. $(K \div p) \cup \{ { \& }K^{\prime } \rightarrow p\} \vdash p$. Then equivalently $K \div p \vdash { \& }K^{\prime } \vee p$. Since Recovery and Inclusion yield $K \div p \vdash p \rightarrow { \& }K^{\prime }$ we would then have $K \div p \vdash { \& }K^{\prime }$, contrary to our assumption $K \div p \subset K^{\prime }$. We can conclude that $X \nvdash p$.

Recovery yields $K \div ({ \& }X \rightarrow { \& }K) \vdash ({ \& }X \rightarrow { \& }K) \rightarrow { \& }K$, and since $\vdash { \& }K \rightarrow { \& }X$ it follows that $K \div ({ \& }X \rightarrow { \& }K) \vdash { \& }X$, hence $X \subseteq K \div ({ \& }X \rightarrow { \& }K)$, hence $K \div p \subseteq K \div ({ \& }X \rightarrow { \& }K)$.

It follows from $K \div p \subset K^{\prime } \nvdash p$ that ${ \& }K^{\prime } \rightarrow p \notin K \div p$. From this and ${ \& }K^{\prime } \rightarrow p \in X \subseteq K \div ({ \& }X \rightarrow { \& }K)$ it follows that $K \div ({ \& }X \rightarrow { \& }K) \nsubseteq K \div p$. Since we already have $K \div p \subseteq K \div ({ \& }X \rightarrow { \& }K)$ we can conclude that $K \div p \subset K \div ({ \& }X \rightarrow { \& }K)$, i.e. $K \div p \subset K^{\prime \prime }$.

Suppose that $K \div ({ \& }X \rightarrow { \& }K) \vdash p$. Since $K \div p \subseteq K \div ({ \& }X \rightarrow { \& }K)$ it would then follow from Recovery and Closure that $K \div ({ \& }X \rightarrow { \& }K) = K$. Success would then yield $\vdash { \& }X \rightarrow { \& }K$, contrary to $X \nvdash p$ that was shown above. Hence $K \div ({ \& }X \rightarrow { \& }K) \nvdash p$, i.e. $K^{\prime \prime } \nvdash p$.

Finally, it follows from ${ \& }K^{\prime } \rightarrow p \in X \subseteq K \div ({ \& }X \rightarrow { \& }K)$ that $K^{\prime } \cup K \div ({ \& }X \rightarrow { \& }K) \vdash p$. In summary, we have shown that $K \div p \subset K^{\prime \prime } \nvdash p$ and $K^{\prime } \cup K^{\prime \prime } \vdash p$, as desired.

Maximality $\Rightarrow$ Preservativity: ¹⁵ Let Maximality hold and let $K^{\prime } \nsubseteq K \div p$. Let $K^{\prime \prime } = K \div p$. It follows from Failure and Inclusion that $p \notin \mathrm{Cn}(\varnothing )$. Therefore it follows from Success that $K^{\prime \prime }$ does not induce $p$ in $K$. On the other hand, since $K \div p$ is a maximal $p$-excluder in $\mathcal{K }$, any element of $\mathcal{K }$ that contains $(K \div p) \cup K^{\prime }$ must contain $p$.

Maximality $\Rightarrow$ Defeasible Maximality: Directly from the definitions.

Part II, Negative Results:

1. Recovery $\Rightarrow \!\!\!\!\!\!\!/$   Maximality: Let $\div$ be (direct) full meet contraction. That it satisfies Recovery is a standard result (Alchourrón et al. (1985); Hansson 1999, p. 123.)

2. Maximality $\Rightarrow \!\!\!\!\!\!\!/$   Recovery: Let $\mathcal{K } = \{\mathrm{Cn}(\varnothing ), K\}$ and let $\div$ be such that $K \div p = \mathrm{Cn}(\varnothing )$ if and only if $p \in K \setminus \mathrm{Cn}(\varnothing )$.

3. Weak Preservativity $\Rightarrow \!\!\!\!\!\!\!\!\!\!/$   Preservativity: Let $K = \mathrm{Cn}(\{a,b,c\})$ and $\mathcal{K } = \{K, \mathrm{Cn}(\{a,b\}), \mathrm{Cn}(\{b,c\}), \mathrm{Cn}(\{a,c\}), \mathrm{Cn}(\{a\}), \mathrm{Cn}(\{b\}), \mathrm{Cn}(\{c\}), \mathrm{Cn}(\varnothing )\}$. Let $K \div (a \& (b \vee c)) = \mathrm{Cn}(\{b\})$, and for all other sentences $p \in K \setminus \mathrm{Cn}(\varnothing )$ let $K \div p$ be a maximal $p$-excluder in $\mathcal{K }$. For all $p \notin K \setminus \mathrm{Cn}(\varnothing )$ let $K \div p = K$.

Proof that Weak Preservativity holds: Let $K^{\prime } \nsubseteq K \div p$. We have to show that there is some $K^{\prime \prime }$ such that $K^{\prime \prime } \cup K^{\prime }$ but not $K^{\prime \prime }$ induces $p$ in $\mathcal{K }$. Due to the construction of $\div$, either $K \div p$ is a maximal $p$-excluder in $\mathcal{K }$ or $p = a \& (b \vee c)$. If $K \div p$ is a maximal $p$-excluder in $\mathcal{K }$, then $(K \div p) \cup K^{\prime }$, being a proper superset of $K \div p$, induces $p$. In the other case we have $K \div (a \& (b \vee c)) = \mathrm{Cn}(\{b\})$. For each $K^{\prime } \in \mathcal{K }$ such that $K^{\prime } \nsubseteq K\div (a \& (b \vee c))$ we can find some $K^{\prime \prime }$ such that $K^{\prime } \cup K^{\prime \prime } \vdash a \& (b \vee c)$, whereas $K^{\prime \prime } \nvdash a \& (b \vee c)$: If $K^{\prime }$ is $\mathrm{Cn}(\{c\})$ or $\mathrm{Cn}(\{b, c\})$, then let $K^{\prime \prime } = \mathrm{Cn}(\{a\})$. If $K^{\prime }$ is either $K$, $\mathrm{Cn}(\{a\})$, $\mathrm{Cn}(\{a,b \})$, or $\mathrm{Cn}(\{a,c\})$ then let $K^{\prime \prime } = \mathrm{Cn}(\{ b \})$.

Proof that Preservativity does not hold: Let $K^{\prime } = \mathrm{Cn}(\{c\})$. We then have $K^{\prime } \nsubseteq K \div ( a \& (b \vee c))$. However, there is no $K^{\prime \prime }$ such that $K\div (a \& (b \vee c)) \subseteq K^{\prime \prime }$, $K^{\prime \prime } \nvdash a \& (b \vee c)$ and $K^{\prime \prime } \cup K^{\prime }$ induces $a \& (b \vee c)$.

4. Preservativity $\Rightarrow \!\!\!\!\!\!\!\!/$   Defeasible Maximality: Let $K = \mathrm{Cn}(\{a,b\})$ and let $\mathcal{K } = \{\mathrm{Cn}(\{a,b\}), \mathrm{Cn}(\{a \vee b\}), \mathrm{Cn}(\{a \rightarrow b\}), \mathrm{Cn}(\varnothing )\}$. Let $K \div a = \mathrm{Cn}(\varnothing )$, and for all other $p \in K \setminus \mathrm{Cn}(\varnothing )$ let $K \div p$ be a maximal $p$-excluder in $\mathcal{K }$. (It will then be either $\mathrm{Cn}(\{a \rightarrow b\})$ or $\mathrm{Cn}(\{a \vee b\})$.) For all $p \notin K \setminus \mathrm{Cn}(\varnothing )$ let $K \div p = K$.

Proof that Preservativity holds: Let $K^{\prime } \nsubseteq K \div p$. There are five cases:

Case i, $K \div p = \mathrm{Cn}(\varnothing )$. Then $p = a$. If $K^{\prime } = \mathrm{Cn}(\{a \rightarrow b\})$ or $K^{\prime } = \mathrm{Cn}(\{a, b\})$, then let $K^{\prime \prime } = \mathrm{Cn}(\{a \vee b\})$. If $K^{\prime } = \mathrm{Cn}(\{a \vee b\})$, then let $K^{\prime \prime } = \mathrm{Cn}(\{a \rightarrow b\})$. (Note that $\mathrm{Cn}(\{a \vee b\}) \cup \mathrm{Cn}(\{a \rightarrow b\})$ induces $a$ in $\mathcal{K }$ without implying $a$.)

Case ii, $K \div p = \mathrm{Cn}(\{a \rightarrow b\})$ and $K^{\prime } = \mathrm{Cn}(\{a \vee b\})$. Let $K^{\prime \prime } = K \div p$. Then $K \div p$ does not imply $p$, thus it does not induce $p$. However $K^{\prime } \cup K^{\prime \prime }$ is a proper superset of $K \div p$, and since $K \div p$ is a maximal $p$-excluder it follows that $K^{\prime } \cup K^{\prime \prime }$ induces $p$.

Case iii, $K \div p = \mathrm{Cn}(\{a \rightarrow b\})$ and $K^{\prime } = \mathrm{Cn}(\{a, b\})$: Let $K^{\prime \prime } = K \div p$.

Case iv, $K \div p = \mathrm{Cn}(\{a \vee b\})$ and $K^{\prime } = \mathrm{Cn}(\{a \rightarrow b\})$. Similar to case ii.

Case v, $K \div p = \mathrm{Cn}(\{a \vee b\})$ and $K^{\prime } = \mathrm{Cn}(\{a, b\})$: Let $K^{\prime \prime } = K \div p$.

Proof that Defeasible Maximality does not hold: Let $K^{\prime } = \mathrm{Cn}(\{a \rightarrow b\})$. We have $K \div a \subset K^{\prime } \nvdash a$. Let $K^{\prime \prime }$ be such that $K \div a \subset K^{\prime \prime } \nvdash a$. Then either $K^{\prime \prime } = \mathrm{Cn}(\{a \rightarrow b\})$ or $K^{\prime \prime } = \mathrm{Cn}(\{a \vee b\})$. In neither of these cases does it hold that $K^{\prime } \cup K^{\prime \prime } \vdash a$.

5. Defeasible Maximality $\Rightarrow \!\!\!\!\!\!\!/$   Weak Preservativity: Let $K = \mathrm{Cn}(\{a, b\})$. Let $\mathcal{K } = \{\mathrm{Cn}(\{a,b\}), \mathrm{Cn}(\{a\}), \mathrm{Cn}(\{b\}), \mathrm{Cn}(\{a \vee b \vee c\}), \mathrm{Cn}(\{a \vee b \vee \lnot c\})\}$. Let $K \div (a \& b) = \mathrm{Cn}(\{a \vee b \vee c\})$ and otherwise let $K \div p$ be an inclusion-maximal $p$-excluder unless $p \in \mathrm{Cn}(\varnothing )$ in which case $K \div p = K$.

Proof that Defeasible Maximality holds: Let $K \div p \subset K^{\prime } \nvdash p$. Then $p = a \& b$ and $K^{\prime }$ is either $\mathrm{Cn}(\{a\})$ or $\mathrm{Cn}(\{b\})$. In the former case, let $K^{\prime \prime } = \mathrm{Cn}(\{b\})$ and in the latter case let $K^{\prime \prime } = \mathrm{Cn}(\{a\})$.

Proof that Weak Preservativity does not hold: Let $K^{\prime } = \mathrm{Cn}(\{a \vee b \vee \lnot c\})$. Then $K^{\prime } \nsubseteq K \div (a \& b)$. Let $K^{\prime \prime }$ be an element of $\mathcal{K }$ that does not induce $a \& b$. Then $K^{\prime \prime }$ is either $\mathrm{Cn}(\{a\})$, $\mathrm{Cn}(\{b\})$, $\mathrm{Cn}(\{a \vee b \vee c\})$, or $\mathrm{Cn}(\{a \vee b \vee \lnot c\})$. In neither case does $K^{\prime \prime } \cup K^{\prime }$ induce $a \& b$.

6. Preservativity $\Rightarrow \!\!\!\!\!\!\!/$   Recovery: Suppose not. We then have Maximality $\Rightarrow$ Preservativity $\Rightarrow$ Recovery, contrary to (2).

7. Preservativity $\Rightarrow \!\!\!\!\!\!\!/$   Maximality: Suppose not. Then: Recovery $\Rightarrow$ Preservativity $\Rightarrow$ Maximality, contrary to (1).

8. Weak Preservativity $\Rightarrow \!\!\!\!\!\!\!/$   Recovery: Suppose not. Then: Weak Preservativity $\Rightarrow$ Recovery $\Rightarrow$ Preservativity, contrary to (3).

9.Weak Preservativity $\Rightarrow \!\!\!\!\!\!\!/$   Maximality: Suppose not. Then: Weak Preservativity $\Rightarrow$ Maximality $\Rightarrow$ Preservativity, contrary to (3).

10. Weak Preservativity $\Rightarrow \!\!\!\!\!\!\!/$   Defeasible Maximality: Suppose not. Then: Preservativity $\Rightarrow$ Weak Preservativity $\Rightarrow$ Defeasible Maximality, contrary to (4).

11. Defeasible Maximality $\Rightarrow \!\!\!\!\!\!\!/$   Recovery: Suppose not. Then: Maximality $\Rightarrow$ Defeasible Maximality $\Rightarrow$ Recovery, contrary to (2).

12. Defeasible Maximality $\Rightarrow \!\!\!\!\!\!\!/$   Maximality: Suppose not. Then: Recovery $\Rightarrow$ Defeasible Maximality $\Rightarrow$ Maximality, contrary to (1).

13. Defeasible Maximality $\Rightarrow \!\!\!\!\!\!\!/$   Preservativity: Suppose not. Then: Defeasible Maximality $\Rightarrow$ Preservativity $\Rightarrow$ Weak Preservativity, contrary to (5).

Proof of Theorem 2

From (1) to (2): According to Theorem 5 of Hansson (2012a), for $\mathcal{K }$ to be the outcome set of a base-generated kernel contraction it must satisfy integrity and excluder merge. It follows directly from the definition of base-generated kernel contraction that it satisfies Success.

In order to prove that base-generated kernel contraction satisfies Weak Preservativity, let $\sigma$ be an incision function for the belief base $B$, let $K = \mathrm{Cn}(B)$, and let $K^{\prime } \nsubseteq K {\mathop {\approx }\limits ^{\frown }}_\sigma p$. Then there is some $z \in B$ such that $z \in K^{\prime }$ and $z \notin K {\mathop {\approx }\limits ^{\frown }}_\sigma p$, consequently $z \notin B \approx _\sigma p$, hence $z \in \sigma (B \bot \!\!\!\bot p)$, hence $z \in \bigcup (B \bot \!\!\!\bot p)$. It follows from Lemma 6 that there is some $X$ such that $z \notin X \in B \perp p$, from Lemma 4 that there is some $q$ such that $\{X\} = B \perp q$ and then from Lemma 8 that $B \approx _\sigma q = X$, hence $\mathrm{Cn}(X) \in \mathcal{K }$. Then $\mathrm{Cn}(X)$ is a maximal $p$-excluder in $\mathcal{K }$. Since $z \in B$ and $X$ is a $B$-closed subset of $B$, it follows from $z \notin X$ that $z \notin \mathrm{Cn}(X)$. Clearly, $\mathrm{Cn}(X) \nvdash p$ but $\mathrm{Cn}(X) \cup \{z\} \vdash p$, thus $\mathrm{Cn}(X) \cup K^{\prime } \vdash p$. It follows that $\mathrm{Cn}(X) \cup K^{\prime }$ but not $\mathrm{Cn}(X)$ induces $p$ in $\mathcal{K }$.

In order to prove that base-generated kernel contraction satisfies Symmetry, let $K {\mathop {\approx }\limits ^{\frown }}_{\sigma } p \ne K {\mathop {\approx }\limits ^{\frown }}_\sigma q$. We need to show that there is some $r$ for which it does not hold that $K {\mathop {\approx }\limits ^{\frown }}_\sigma r \vdash p$ if and only if $K {\mathop {\approx }\limits ^{\frown }}_\sigma r \vdash q$. It follows from $K {\mathop {\approx }\limits ^{\frown }}_{\sigma } p \ne K {\mathop {\approx }\limits ^{\frown }}_\sigma q$ that $B \approx _{\sigma } p \ne B \approx _\sigma q$ and thus $B \bot \!\!\!\bot p \ne B \bot \!\!\!\bot q$. Due to Lemma 5, $B \perp p \ne B \perp q$. Without loss of generality we may assume that there is some $X\in B \perp p$ such that $X\notin B \perp q$. There are two cases: Case 1, $X\vdash q$: Due to Lemma 4 there is some $r$ such that $\{X \}= B \perp r$. Lemma 8 yields $B \approx _\sigma r=X$, so that $B \approx _\sigma r \nvdash p$ and $B \approx _\sigma r \vdash q$, hence $K {\mathop {\approx }\limits ^{\frown }}_\sigma r \nvdash p$ and $K {\mathop {\approx }\limits ^{\frown }}_\sigma r \vdash q$. Case 2, $X\nvdash q$. Then, since $B$ is finite, there is some $X^{\prime }$ such that $X\subset X ^{\prime }\in B \perp q$. It follows from Lemma 4 that there is some $r$ such that $\{X ^{\prime }\}= B \perp r$ and from Lemma 8 that $B \approx _\sigma r =X^{\prime }$. It follows that $B \approx _\sigma r \vdash p$ and $B \approx _\sigma r \nvdash q$, thus $K {\mathop {\approx }\limits ^{\frown }}_\sigma r \vdash p$ and $K {\mathop {\approx }\limits ^{\frown }}_\sigma r \nvdash q$.

From (2) to (1): It follows from integrity that $K \in \mathcal{K }$. Let $B = \{ { \& }K^{\prime } \mid K^{\prime } \in \mathcal{K }\}$ and let $\sigma$ be the function such that for all $p \in K \setminus \mathrm{Cn}(\varnothing )$:

$\sigma (B \bot \!\!\!\bot p) = \{q \in B \mid K \div p \nvdash q \}$

We have to show (i) that $\sigma$ is a well-defined function, (ii) that $\sigma$ is an incision function on $B$, and (iii) that $K \div p = \mathrm{Cn}(B \setminus \sigma (B \bot \!\!\!\bot p))$ for all $p$.

To prove (i), we need to show that if $B \bot \!\!\!\bot p = B \bot \!\!\!\bot p^{\prime }$ then $\sigma (B \bot \!\!\!\bot p) = \sigma (B \bot \!\!\!\bot p^{\prime })$. Let $B \bot \!\!\!\bot p = B \bot \!\!\!\bot p^{\prime }$. It follows from Lemma 5 and Symmetry that $K \div p = K \div p^{\prime }$, thus $\sigma (B \bot \!\!\!\bot p) = \sigma (B \bot \!\!\!\bot p^{\prime })$.

To prove (ii), we need to show that (ii-a) $\sigma (B \bot \!\!\!\bot p) \subseteq \bigcup (B \bot \!\!\!\bot p)$ and (ii-b) if $\varnothing \ne X \in B \bot \!\!\!\bot p$, then $X \cap \sigma (B \bot \!\!\!\bot p) \ne \varnothing$.

For (ii-a), let $x \in \sigma (B \bot \!\!\!\bot p)$. Then $x \in B$ and $x \notin K \div p$. Due to the construction of $B$ there is some $K_x \in \mathcal{K }$ such that $x =\, { \& }K_x$, hence $K_x \nsubseteq K \div p$. Due to Weak Preservativity there is some $K_m \in \mathcal{K }$ such that $K_m \cup K_x$ but not $K_m$ induces $p$ in $\mathcal{K }$. Then $K_x \nsubseteq K_m$ and ${ \& }K_m \in B$. Since ${ \& }K_m \nvdash p$ there is some $Y$ such that ${ \& }K_m \in Y \in B \perp p$. Due to Lemma 4 there is some $r$ such that $\{Y\} =B \perp r$, thus $Y = \{{ \& }K^{\prime } \mid r \notin K^{\prime } \in \mathcal{K } \}$, and it follows from excluder merge that $\mathrm{Cn}(Y) \in \mathcal{K }$. Since $K_m \cup K_x$ induces $p$ in $\mathcal{K }$, it follows from $K_m \subseteq \mathrm{Cn}(Y) \in \mathcal{K }$ and $Y \nvdash p$ that ${ \& }K_x \notin Y$, thus ${ \& }K_x \notin \bigcap (B \perp p)$, and Lemma 6 yields ${ \& }K_x \in \bigcup (B \bot \!\!\!\bot p)$, i.e. $x \in \bigcup (B \bot \!\!\!\bot p)$ as desired.

For (ii-b), let $\varnothing \ne X \in B \bot \!\!\!\bot p$. Then $\nvdash p$, hence $K \div p \nvdash p$ due to Success. Since $X \vdash p$ we have $X \nsubseteq K \div p$, hence there is then some $x \in X$ such that $K \div p \nvdash x$. Thus $x \in \sigma (B \bot \!\!\!\bot p)$ and consequently $X \cap \sigma (B \bot \!\!\!\bot p) \ne \varnothing$.

For one direction of (iii),we can use ${ \& }(K \div p) \in B$ and ${ \& }(K \div p) \notin \sigma (B \bot \!\!\!\bot p)$ to obtain $K \div p \subseteq \mathrm{Cn}(B \setminus \sigma (B \bot \!\!\!\bot p))$.

For the other direction, suppose to the contrary that $\mathrm{Cn}(B \setminus \sigma (B \bot \!\!\!\bot p)) \nsubseteq K \div p$. Since $K \div p$ is logically closed there is then some $z \in B \setminus \sigma (B \bot \!\!\!\bot p)$ such that $K \div p \nvdash z$. But it follows from $z \in B \setminus \sigma (B \bot \!\!\!\bot p)$ and the definition of $\sigma$ that $K \div p \vdash z$. We can conclude from this contradiction that $\mathrm{Cn}(B \setminus \sigma (B \bot \!\!\!\bot p)) \subseteq K \div p$.

Proof of Theorem 3

From (1) to (2): According to Theorem 5 of Hansson (2012a), for $\mathcal{K }$ to be the outcome set of a base-generated partial meet contraction it must satisfy integrity and excluder merge. It follows directly from the definition of base-generated partial meet contraction that it satisfies Success. Since partial meet contraction is a special case of kernel contraction, it follows from Theorem 2 that Symmetry holds.

In order to prove that Preservativity holds, let $\gamma$ be a selection function for the belief base $B$, let $K = \mathrm{Cn}(B)$, and let $K^{\prime } \nsubseteq K {\mathop {\sim }\limits ^{\frown }}_\gamma p$. Then there is some $z \in B$ such that $z \in K^{\prime }$ and $z \notin K {\mathop {\sim }\limits ^{\frown }}_\gamma p$, consequently $z \notin B \sim _\gamma p$. It follows that there is some $X$ such that $B \sim _\gamma p\subseteq X \in B \perp p$ and $z \notin X$. It follows from Lemma 4 that there is some $q$ such that $\{X\} = B \perp q$, hence $X = B \sim _\gamma q$, hence $\mathrm{Cn}(X) \in \mathcal{K }$. Then $K {\mathop {\sim }\limits ^{\frown }}_\gamma p \subseteq \mathrm{Cn}(X) \nvdash p$ and $\mathrm{Cn}(X) \cup \{z\} \vdash p$, hence $\mathrm{Cn}(X) \cup K^{\prime } \vdash p$. It follows that $\mathrm{Cn}(X) \cup K^{\prime }$ but not $\mathrm{Cn}(X)$ induces $p$ in $\mathcal{K }$.

From (2) to (1): It follows from integrity that $K \in \mathcal{K }$. Let $B = \{ { \& }K^{\prime } \mid K^{\prime } \in \mathcal{K }\}$ and let $\gamma$ be the function such that for all $p \notin \mathrm{Cn}(\varnothing )$,

$\gamma (B \perp p) = \{ K^{\prime } \cap B \mid (K^{\prime } \in \mathcal{K }) \mathrm{\ and \ } (K\div p \subseteq K^{\prime } \nvdash p) \mathrm{\ and \ } \lnot (\exists K^{\prime \prime } \in \mathcal{K })( K^{\prime } \subset K^{\prime \prime } \nvdash p) \}$

and that $\gamma (B \perp p) = \{B\}$ if $p \in \mathrm{Cn}(\varnothing )$. We have to show (i) that $\gamma$ is a well-defined function, (ii) that $\gamma$ is a selection function on $B$, and (iii) that $K \div p = \mathrm{Cn}( \cap \gamma (B \perp p))$.

To prove (i), we need to show that if $B \perp p = B \perp p^{\prime }$ then $\gamma (B \perp p) = \gamma (B \perp p^{\prime })$. Let $B \perp p = B \perp p^{\prime }$. It follows from Lemma 5 and Symmetry that $K \div p = K \div p^{\prime }$, thus $\gamma (B \perp p) = \gamma (B \perp p^{\prime })$.

To prove (ii) we need to show that, whenever $p \notin \mathrm{Cn}(\varnothing )$ and $X \in \gamma (B \perp p)$, then (ii-a) $X \subseteq B$, (ii-b) $X \nvdash p$, and (ii-c) there is no $Y$ such that $X \subset Y \subseteq B$ and $Y \nvdash p$. Furthermore we need to show that (ii-d) $\gamma (B \perp p) \ne \varnothing$ whenever $B \perp p \ne \varnothing$.

(ii-a) and (ii-b) follow directly from the definition. For (ii-c), suppose to the contrary that $X \subset Y \subseteq B$ and $Y \nvdash p$. Then there is some $Y^{\prime } \subseteq B$ such that $X \subset Y^{\prime } \in B \perp p$. Due to Lemma 4 there is some $q$ such that $\{Y^{\prime }\} = B \perp q$, thus $Y^{\prime } = \{{ \& }K^{\prime } \mid q \notin K^{\prime } \in \mathcal{K } \}$. It follows from excluder merge that $\mathrm{Cn}(Y^{\prime }) \in \mathcal{K }$. Since $X$ and $Y^{\prime }$ are $B$-closed and $X \subset Y^{\prime }$ we then have $\mathrm{Cn}(X) \subset \mathrm{Cn}(Y^{\prime }) \nvdash p$, contrary to $X \in \gamma (B \perp p)$. It follows from this contradiction that there is no $Y$ such that $X \subset Y \subseteq B$ and $Y \nvdash p$.

For (ii-d): When $B \perp p$ is non-empty then $p \notin \mathrm{Cn}(\varnothing )$. It then follows from Success that there is some $K^{\prime } \in \mathcal{K }$ such that $K \div p \subseteq K^{\prime } \nvdash p$ (namely $K^{\prime }= K \div p$), thus there is some inclusion-maximal such $K^{\prime }$, thus $\gamma (B \perp p)$ is non-empty.

For one direction of (iii) note that ${ \& }(K\div p)$ is an element of all elements of $\gamma (B \perp p)$, thus $K \div p \subseteq \mathrm{Cn}( \cap \gamma (B \perp p))$.

For the other direction, suppose to the contrary that $\mathrm{Cn}( \cap \gamma (B \perp p)) \nsubseteq K \div p$. Then since $K \div p$ is logically closed there is some $z \in \cap \gamma (B \perp p)$ such that $z \notin K \div p$. Since $z \in B$ there is some $K_z \in \mathcal{K }$ such that $z = { \& }K_z$. Thus $K_z \nsubseteq K \div p$, and it follows from Preservativity that there is some $K_m \in \mathcal{K }$ such that $K \div p \subseteq K_m$ and that $K_m \cup K_z$ but not $K_m$ induces $p$ in $\mathcal{K }$. Then ${ \& }K_m \in B$, and there is some $Y$ such that ${ \& }K_m \in Y \in B \perp p$. It follows from Lemma 4 that there is some $r$ such that $\{Y\} = B \perp r$, thus $Y = \{{ \& }K^{\prime } \mid r \notin K^{\prime } \in \mathcal{K } \}$, and it follows from excluder merge that $\mathrm{Cn}(Y) \in \mathcal{K }$. Since $K_m \cup K_z$ induces $p$ in $\mathcal{K }$ it follows from $K_m \subseteq \mathrm{Cn}(Y)$ that $K_z \nsubseteq \mathrm{Cn}(Y)$, thus ${ \& }K_z \notin Y$. It follows from our definition of $\gamma$ (substituting $\mathrm{Cn}(Y)$ for $K^{\prime }$ and noting that $\mathrm{Cn}(Y) \cap B = Y$) that $Y \in \gamma (B\perp p)$, thus ${ \& }K_z \notin \bigcap \gamma (B \perp p)$, contrary to the assumption.

Proof of Theorem 4

From (1) to (2): Since maxichoice contraction is a special case of partial meet contraction, it follows from Theorem 3 that $\mathcal{K }$ satisfies integrity and excluder merge and that $\div$ satisfies Success, and Symmetry. In order to show that Maximality is satisfied,let $\sim _\gamma$ be a maxichoice contraction and let $K {\mathop {\sim }\limits ^{\frown }}_\gamma p \subset K^{\prime }$. Since $K {\mathop {\sim }\limits ^{\frown }}_\gamma p$ and $K^{\prime }$ are both logical closures of subsets of $B$ it follows that $B \sim _\gamma p = B \cap (K {\mathop {\sim }\limits ^{\frown }}_\gamma p) \subset B \cap K^{\prime }$. Since $\sim _\gamma$ is maxichoice we then have $B \cap K^{\prime } \vdash p$, thus $K^{\prime } \vdash p$.

From (2) to (1): It follows from integrity that $K \in \mathcal{K }$. Let $B = \{ { \& }K^{\prime } \mid K^{\prime } \in \mathcal{K }\}$ and let $\gamma$ be the function such that for all $p \notin \mathrm{Cn}(\varnothing )$:

$\gamma (B \perp p) = \{X \mid { \& }(K \div p) \in X \in B \perp p \}$

and that $\gamma (B \perp p) = \{B\}$ if $p \in \mathrm{Cn}(\varnothing )$. We need to show (i) that $\gamma$ is a well-defined function, (ii) that $\gamma$ is a maxichoice selection function on $B$, and (iii) that $K \div p = \mathrm{Cn}( \bigcap \gamma (B \perp p))$.

To prove (i), we need to show that if $B \perp p = B \perp p^{\prime }$ then $\gamma (B \perp p) = \gamma (B \perp p^{\prime })$. Let $B \perp p = B \perp p^{\prime }$. It follows from Lemma 5 and Symmetry that $K \div p = K \div p^{\prime }$, thus $\gamma (B \perp p) = \gamma (B \perp p^{\prime })$.

To prove (ii) it is, given the construction of $\gamma$, sufficient to prove (ii-a) that $\gamma (B \perp p)$ is non-empty whenever $B \perp p$ is non-empty, and (ii-b) $\bigcap \gamma (B \perp p) \in B \perp p$. (ii-a) follows from Success. For (ii-b), suppose to the contrary that $\bigcap \gamma (B \perp p) \notin B \perp p$. Then there is some $Y$ such that $\bigcap \gamma (B \perp p) \subset Y \in B \perp p$. Due to Lemma 4 there is some $q$ such that $\{Y\} = B \perp q$, thus $Y = \{z \in B \mid z \nvdash q\} = \{ { \& }K^{\prime } \mid q \notin K^{\prime } \in \mathcal{K } \}$, and excluder merge yields $\mathrm{Cn}(Y) \in \mathcal{K }$. Since both $\bigcap \gamma (B \perp p)$ and $Y$ are $B$-closed, it follows from $\bigcap \gamma (B \perp p) \subset Y$ that $\mathrm{Cn}(\bigcap \gamma (B \perp p)) \subset \mathrm{Cn}(Y)$. Since ${ \& }(K \div p) \in \bigcap \gamma (B \perp p)$ we then obtain $K \div p \subset \mathrm{Cn}(Y) \nvdash p$, contrary to Maximality.

To prove (iii), note that due to the construction of $\gamma$, $B \cap (K \div p) \subseteq \bigcap \gamma (B \perp p)$. Suppose that $B \cap (K \div p) \subset \bigcap \gamma (B \perp p)$. Then there is some $B$-closed set $Y$ such that $B \cap (K \div p) \subset Y \in B \perp p$, and it follows in the same way as in part (ii) that $\mathrm{Cn}(Y) \in \mathcal{K }$. We have $\mathrm{Cn}(B \cap (K \div p)) = K \div p$, and since both $Y$ and $B \cap (K \div p)$ are $B$-closed it follows from $B \cap (K \div p) \subset Y$ that $\mathrm{Cn}(B \cap (K \div p)) \subset \mathrm{Cn}(Y)$, hence $K \div p \subset \mathrm{Cn}(Y) \nvdash p$, contrary to Maximality.

Proof of Theorem 5

From (1) to (2): Since full meet contraction is a special case of kernel contraction, it follows from Theorem 2 that $\mathcal{K }$ satisfies integrity and excluder merge and that $\div$ satisfies Weak Preservativity.

In order to show that Combinative Success is satisfied, let $p \notin K^{\prime } \in \mathcal{K }$. Due to the construction, $K^{\prime } = K {\mathop {\sim }\limits ^{\frown }} q = \mathrm{Cn}(B \sim q)$ for some $q$. It follows from $B \sim q \nvdash p$ that there is some $X$ such that $B \sim q \subseteq X \in B \perp p$. Since $B \sim p \subseteq X$ it follows that $(B \sim q) \cup (B \sim p) \nvdash p$, hence $K^{\prime } \cup (K {\mathop {\sim }\limits ^{\frown }} p) \nvdash p$.

From (2) to (1): It follows from integrity that $K \in \mathcal{K }$. Let $B = \{ { \& }K^{\prime } \mid K^{\prime } \in \mathcal{K }\}$. We are going to show that $\mathrm{Cn}(\cap (B \perp p)) = K \div p$.

For one direction, let $X \in B \perp p$. Due to Lemma 4 there is some $q$ such that $\{X\} = B \perp q$, hence $X = \{{ \& }K^{\prime } \mid q \notin K^{\prime } \in \mathcal{K } \}$, and excluder merge yields $\mathrm{Cn}(X) \in \mathcal{K }$. Combinative Success yields $\mathrm{Cn}(X) \cup (K \div p) \nvdash p$, and it follows from $X \in B \perp p$ that ${ \& }(K \div p) \in X$. Since this holds for all $X \in B \perp p$, we have ${ \& }(K\div p) \in \bigcap (B \perp p)$, thus $K\div p \subseteq \mathrm{Cn}( \bigcap (B \perp p))$.

For the other direction, we first need to show that if $K_y$ is a maximal $p$-excluder in $\mathcal{K }$, then $B \cap K_y \in B \perp p$. Suppose not. Then there is some $V$ such that $B \cap K_y \subset V \in B \perp p$. Due to Lemma 4 there is some $q$ such that $\{V\} = B \perp q$, hence $V = \{{ \& }K^{\prime } \mid q \notin K^{\prime } \in \mathcal{K } \}$, and excluder merge yields $\mathrm{Cn}(V) \in \mathcal{K }$. It follows from $B \cap K_y \subset V$ and the $B$-closure of $B \cap K_y$ and $V$ that $\mathrm{Cn}(B \cap K_y) \subset \mathrm{Cn}(V)$, equivalently $K_y \subset \mathrm{Cn}(V)$, contrary to the assumption that $K_y$ is a maximal $p$-excluder. We can conclude that for any maximal $p$-excluder $K_y$, $B \cap K_y \in B \perp p$.

Now let $z \in \bigcap (B \perp p)$. There is then some $K_z \in \mathcal{K }$ such that $z = { \& }K_z$. Since ${ \& }K_z \in \bigcap (B \perp p)$ it follows that $K_z$ is a subset of every maximal $p$-excluder in $\mathcal{K }$, and Weak Preservativity yields $K_z \subseteq K \div p$, hence $z \in B \cap (K \div p)$. Hence $\bigcap (B \perp p) \subseteq B \cap (K \div p)$, hence $\mathrm{Cn}(\cap (B \perp p)) \subseteq K \div p$.

Proof of Theorem 6

From (1) to (2): It follows from Theorem 3 of Hansson (2012a) that $\mathcal{K }$ satisfies integrity and retainability. It follows from the definition that direct partial meet contraction satisfies Success and Failure. That it satisfies Recovery is a standard result from Alchourrón et al. (1985).

Symmetry will be proved in its converse form. Let $K\div p \ne K \div q$. Since $\div$ is a partial meet contraction, it follows that $K\perp p \ne K \perp q$. We can assume without loss of generality that there is some $X$ such that $X \in K \perp p \setminus K \perp q$. There are two cases.

Case 1, $X \vdash q$: Due to compactness and the logical closure of $X$ there is some $x \in X$ such that $x \vdash q$. Since $X \in K \perp p$ we also have $p \rightarrow { \& }K \in X$, thus $x \ \& (p \rightarrow { \& }K) \in X \in K \perp p$. Due to retainability there is some $K^{\prime } \in \mathcal{K }$ such that $x \ \& (p \rightarrow { \& }K) \in K^{\prime } \subset K$. Then $K^{\prime } \nvdash p$ and $K^{\prime } \vdash q$.

Case 2, $X \nvdash q$: Due to Lemma 1 there is some $Z$ such that $X \subset Z \in K \perp q$. Clearly, $Z \vdash p$ and due to compactness there is some $z \in Z$ such that $z \vdash p$. We have $z \ \& (q \rightarrow { \& }K) \in Z \in K \perp q$, and due to retainability there is some $K^{\prime } \in \mathcal{K }$ such that $z \ \& (q \rightarrow { \& }K) \in K^{\prime } \subset K$. Then $K^{\prime } \nvdash q$ and $K^{\prime } \vdash p$.

From (2) to (1): It follows from integrity that $K \in \mathcal{K }$. Let $\gamma$ be a function such that for all $p \notin \mathrm{Cn}(\varnothing )$:

$$\begin{aligned} \gamma (K \perp p) = \{X \in K \perp p \mid K \div p \subseteq X \} \end{aligned}$$

and that $\gamma (K \perp p) = \{K\}$ if $p \in \mathrm{Cn}(\varnothing )$. We need to show (1) that $\gamma$ is a (well-defined) function, (2) that $\gamma$ is a selection function, and (3) that for all $p$: $K \div p = \bigcap \gamma (K \perp p)$.

Part 1: In order for $\gamma$ to be a function, it must be the case that for all $p$ and $q$, if $K\perp p= K \perp q$, then $\gamma (K\perp p) = \gamma ( K \perp q)$. Let $K\perp p= K \perp q$. It follows from Lemma 5 and Symmetry that $K \div p = K \div q$, and then from the definition of $\gamma$ that $\gamma (K\perp p) = \gamma ( K \perp q)$.

Part 2: In order for $\gamma$ to be a selection function, it must be the case that if $K \perp p \ne \varnothing$ then (i) $\gamma (K\perp p) \subseteq K \perp p$ and (ii) $\gamma (K\perp p) \ne \varnothing$. (i) follows directly from the definition. For (ii), let $K \perp p \ne \varnothing$. Then $\nvdash p$, and Success yields $K \div p \nvdash p$. It follows from Lemma 1 that there is some $X$ such that $K \div p \subseteq X \in K \perp p$, and then $X \in \gamma (K \perp p)$.

Part 3: It follows directly from the definition that $K \div p \subseteq \bigcap \gamma (K \perp p)$. In order to show that $\bigcap \gamma (K \perp p) \subseteq K \div p$, let $z \in K \setminus (K \div p)$. Since ${ \& }K \vdash z$, $z$ is equivalent with $(z \rightarrow { \& }K) \rightarrow { \& }K$, thus $K\div p \nvdash (z \rightarrow { \& }K) \rightarrow { \& }K$, thus ${ \& }(K \div p)\ \& \ (z \rightarrow { \& }K) \nvdash { \& }K$. Due to retainability there is some $K^{\prime }$ such that ${ \& }(K \div p)\ \& \ (z \rightarrow { \& }K) \in K^{\prime } \subset K$. Due to Recovery, $K^{\prime } \nvdash p$. Due to Lemma 1 there is some $Y$ such that $K^{\prime } \subseteq Y \in K \perp p$, and since $z \rightarrow { \& }K \in Y$ we have $z \notin Y$. It follows from $z \notin Y \in \gamma (K \perp p)$ that $z \notin \bigcap \gamma (K \perp p)$.

Proof of Theorem 7

From (1) to (2): Given Theorem 6 it remains to show that $\sim$ satisfies Eradication Success. Let $q \in (K \sim p) \cap \mathrm{Cn}(\{p\})$. It follows from Lemma 7 that $q \in \mathrm{Cn}(\{\lnot p\})$, thus $q \in \mathrm{Cn}(\{p\}) \cap \mathrm{Cn}(\{\lnot p\})$, thus due to Lemma 2, $q \in \mathrm{Cn}(\varnothing )$.

From (2) to (1): If $p \notin K$, then Failure yields $K \div p = K$, thus $K \sim p \subseteq K \div p$. If $p \in K$, then due to Recovery, $p \rightarrow { \& }K \in K \div p$, hence due to Lemma 7, $K \sim p \subseteq K \div p$. For the other direction, if $p \notin K$ then $K \sim p = K$, and $K \div p \subseteq K$ follows from $K = \bigcup \mathcal{K }$, thus $K \div p \subseteq K \sim p$. In the case when $p \in K$, let $z \in K \div p$. It follows from Eradication Success that $\mathrm{Cn}(\{z\}) \cap \mathrm{Cn}(\{ p\}) = \mathrm{Cn}(\varnothing )$. Lemma 2 yields $\vdash p \vee z$, equivalently $\lnot p \vdash z$, and Lemma 7 yields $z \in K \sim p$. Hence, $K \div p \subseteq K \sim p$.

Proof of Theorem 8

See Hansson (2007, Observation 2).

Proof of Observation 1

Part 1 follows directly from Lemmas 7 and 2.

Part 2: It follows truth-functionally from ${ \& }K \vdash f(p)$, ${ \& }K \vdash { \& }(K\div p)$ (that follows from Inclusion), and $\vdash { \& }(K \div p) \leftrightarrow (f(p) \rightarrow { \& }K)$ that $\vdash f(p) \leftrightarrow ({ \& }(K \div p) \rightarrow { \& }K)$.