Abstract
Cooper storage is a widespread technique for associating sentences with their meanings, used (sometimes implicitly) in diverse linguistic and computational linguistic traditions. This paper encodes the data structures and operations of cooper storage in the simply typed linear \(\lambda \)-calculus, revealing the rich categorical structure of a graded applicative functor. In the case of finite cooper storage, which corresponds to ideas in current transformational approaches to syntax, the semantic interpretation function can be given as a linear homomorphism acting on a regular set of trees, and thus generation can be done in polynomial time.

















Similar content being viewed by others
Notes
This has nothing to do with endocentricity, or the headedness of syntactic phrases.
Our linguist is using the atomic types e and t [which correspond to the \(\iota \) and o of Church (1940)]. The complex type \(\alpha \beta \) is elsewhere written as \(\alpha \rightarrow \beta \), and juxtaposition is right associative; \(\alpha \beta \gamma \) is \(\alpha (\beta \gamma )\).
The obvious minimal solution, namely, allowing a operation which combines a term of type (et)t with one of type eet (for example \(\lambda m,f,k.m(\lambda x.fxk)\)), will not extend to an account of the ambiguity of sentences with quantifiers.
What exactly this means is discussed in Sect. 1.2.
The retrieval operation is redefined so: \(\text {XP}(\textsc {fa}\ q\ x,X)\mathrel {\hbox {:-}}\mathrm{X}{^{\prime }}({x,\{q\}\cup X})\).
These types can be viewed as right folds over the list p. In particular,
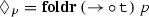 , and
, and  , where
, where  .
.de Groote (1994) presents a translation of the \(\lambda \mu \)-calculus into the \(\lambda \)-calculus, using a continuation passing style transform. From this perspective, continuation-based proposals (developed extensively in Barker and Shan (2014), although there the focus is on delimited continuations) can be viewed as related to the \(\lambda \mu \)-calculus, and thus to cooper-storage.
Notation has been changed from McBride and Paterson (2008). The operator
 (there called pure) lifts a value into a functor type. This is reflected notationally by having the arrow point up. The operator
(there called pure) lifts a value into a functor type. This is reflected notationally by having the arrow point up. The operator  (there written as a binary infix operator
(there written as a binary infix operator  and known as apply) lowers its argument from a function-container to a function over containers, and so the arrow points down. Viewing \(\bigcirc \) as a necessity operator, the type of
and known as apply) lowers its argument from a function-container to a function over containers, and so the arrow points down. Viewing \(\bigcirc \) as a necessity operator, the type of  is familiar as the K axiom, and viewing it as a possibility operator, the type of
is familiar as the K axiom, and viewing it as a possibility operator, the type of 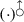 is the axiom T. Lax logic (Fairtlough and Mendler 1997) is the (intuitionistic) modal logic which to the axioms above adds \(\bigcirc \bigcirc \alpha \rightarrow \bigcirc \alpha \) and corresponds via the Curry–Howard correspondance to monads (Moggi 1991; Benton et al. 1998), which are applicative functors enriched with an operation \({\textit{join}} : \bigcirc \bigcirc \alpha \rightarrow \bigcirc \alpha \) satisfying certain conditions.
is the axiom T. Lax logic (Fairtlough and Mendler 1997) is the (intuitionistic) modal logic which to the axioms above adds \(\bigcirc \bigcirc \alpha \rightarrow \bigcirc \alpha \) and corresponds via the Curry–Howard correspondance to monads (Moggi 1991; Benton et al. 1998), which are applicative functors enriched with an operation \({\textit{join}} : \bigcirc \bigcirc \alpha \rightarrow \bigcirc \alpha \) satisfying certain conditions.The parameter arguments will sometimes be suppressed for readability; it is always possible to reconstruct them from the context.
Rather, the equations require only that
 and that
and that 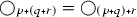 . This is automatic if P is in fact a monoid, but would also be satisfied if, for example, \(\bigcirc \) were the constant function from P into \(\mathcal {T}_A \rightarrow \mathcal {T}_A\).
. This is automatic if P is in fact a monoid, but would also be satisfied if, for example, \(\bigcirc \) were the constant function from P into \(\mathcal {T}_A \rightarrow \mathcal {T}_A\).The applicative functor operations are interdefinable with these, as follows (\(\mathbb {K} = \lambda x,y.x\), \((,) = \lambda x,y.\langle x,y\rangle \), \({\textsf {uncurry}} = \lambda f,x.f (\pi _1 x) (\pi _2 x)\), \({\textsf {app}} = \lambda x,y.xy\), and
 is the empty tuple—the monoidal unit for the product operation).
is the empty tuple—the monoidal unit for the product operation).
While the operations and types involving cooper storage are linear, there is no such guarantee about the objects being so manipulated. A natural way to think about this involves treating the types being manipulated as abstract types [as in abstract categorial grammars de Groote (2001a)], the internal details of which are irrelevant to the storage mechanisms.
Except in the uninteresting case where \(w_i = \alpha \) for some i.
A misguided attempt to generalize the current proposal to arbitrary stores is, when attempting to store something of type
 , to put the entire expression of type
, to put the entire expression of type  into the store (Kobele 2006). This would yield an alternative storage operator
into the store (Kobele 2006). This would yield an alternative storage operator  . (The given
. (The given  would correspond to
would correspond to  .) While such a generalization is logically possible, it is problematic in the sense that there is no obvious way for the other elements in the store to bind what should intuitively be their arguments, which have been abstracted over in the newly stored expression.
.) While such a generalization is logically possible, it is problematic in the sense that there is no obvious way for the other elements in the store to bind what should intuitively be their arguments, which have been abstracted over in the newly stored expression.More precisely,
 is a forest of unranked trees. For
is a forest of unranked trees. For  , \(\epsilon \), \(a(\epsilon )\), and \(a(b(\epsilon ),c(\epsilon )),d(\epsilon )\) are elements of P. The term \(a(\epsilon )\) will be written as a, and so these elements of P will be represented rather as \(\epsilon \), a, and a(b, c), d.
, \(\epsilon \), \(a(\epsilon )\), and \(a(b(\epsilon ),c(\epsilon )),d(\epsilon )\) are elements of P. The term \(a(\epsilon )\) will be written as a, and so these elements of P will be represented rather as \(\epsilon \), a, and a(b, c), d.The rules in the figure are only annotated with a semantic component, the pronounced components remain the same as in Fig. 1.
As in example 2, the rule for retrieve is non-deterministic.
Where size is measured in terms of the sum of the sizes of the types is the store; this bounds as well the maximal size of stored types.
A short Coq development of this proof is available at https://github.com/gkobele/cooper-storage.
References
Atkey, R. (2009). Parameterized notions of computation. Journal of Functional Programming, 19(3–4), 335–376.
Babaev, A. A., & Soloviev, S. V. (1982). A coherence theorem for canonical morphisms in cartesian closed categories. Journal of Soviet Mathematics, 20, 2263–2279.
Barendregt, H., Dekkers, W., & Statman, R. (2013). Lambda calculus with types. Cambridge: Cambridge University Press.
Barker, C., & Shan, C. (2014). Continuations and natural language, Oxford studies in theoretical linguistics (Vol. 53). Oxford: Oxford University Press.
Benton, P. N., Bierman, G. M., & de Paiva, V. (1998). Computational types from a logical perspective. Journal of Functional Programming, 8(2), 177–193.
Büring, D. (2004). Crossover situations. Natural Language Semantics, 12(1), 23–62.
Church, A. (1940). A formulation of the simple theory of types. Journal of Symbolic Logic, 5(2), 56–68.
Cooper, R. (1983). Quantification and syntactic theory. Dordrecht: D. Reidel.
de Groote, P. (1994). A CPS-translation of the \(\lambda \mu \)-calculus. In S. Tison (Ed.), Proceedings of the colloquium on trees in algebra and programming—CAAP’94, lecture notes in computer science (Vol. 787, pp. 85–99). Berlin: Springer.
de Groote, P. (2001a). Towards abstract categorial grammars. In Association for computational linguistics, 39th annual meeting and 10th conference of the European chapter, proceedings of the conference (pp. 148–155).
de Groote, P. (2001b). Type raising, continuations, and classical logic. In R. van Rooy, & M. Stokhof (Eds.), Proceedings of the thirteenth amsterdam colloquium (pp. 97–101). Amsterdam: University of Amsterdam.
de Groote, P., Pogodalla, S., & Pollard, C. (2011). About parallel and syntactocentric formalisms: A perspective from the encoding of convergent grammar into abstract categorial grammar. Fundamenta Informaticae, 106(2–4), 211–231.
Fairtlough, M., & Mendler, M. (1997). Propositional lax logic. Information and Computation, 137(1), 1–33.
Hunter, T. (2010). Relating movement and adjunction in syntax and semantics. Ph.D. thesis, University of Maryland.
Johnson, K. (2000). How far will quantifiers go? In R. Martin, D. Michaels, & J. Uriagereka (Eds.), Step by step: essays on minimalist syntax in honor of Howard Lasnik, chap 5 (pp. 187–210). Cambridge, MA: MIT Press.
Kanazawa, M. (2007). Parsing and generation as datalog queries. In Proceedings of the 45th annual meeting of the association of computational linguistics (ACL) (pp. 176–183). Prague: Association for Computational Linguistics.
Kanazawa, M. (2009). The pumping lemma for well-nested multiple context-free languages. In V. Diekert & D. Nowotka (Eds.), Developments in language theory, lecture notes in computer science (Vol. 5583, pp. 312–325). Berlin: Springer.
Kanazawa, M. (2017). Parsing and generation as Datalog query evaluation. The IfCoLog Journal of Logics and their Applications, 4(4), 1103–1211.
Keller, W. R. (1988). Nested cooper storage: The proper treatment of quantification in ordinary noun phrases. In U. Reyle & C. Rohrer (Eds.), Natural language parsing and linguistic theories, number 35 in studies in linguistics and philosophy (pp. 432–447). Dordrecht: D. Reidel.
Kobele, G. M. (2006). Generating copies: An investigation into structural identity in language and grammar. Ph.D. thesis, University of California, Los Angeles.
Kobele, G. M. (2012). Importing montagovian dynamics into minimalism. In D. Béchet & A. Dikovsky (Eds.), Logical aspects of computational linguistics, lecture notes in computer science (Vol. 7351, pp. 103–118). Berlin: Springer.
Kreisel, G., & Krivine, J. L. (1967). Elements of mathematical logic (model theory). Amsterdam: North-Holland.
Larson, R. K. (1985). Quantifying into NP. http://semlab5.sbs.sunysb.edu/~rlarson/qnp.pdf.
May, R., & Bale, A. (2005). Inverse linking. In M. Everaert & H. van Riemsdijk (Eds.), The Blackwell companion to syntax, chap 36 (Vol. 2, pp. 639–667). Oxford: Blackwell.
McBride, C., & Paterson, R. (2008). Applicative programming with effects. Journal of Functional Programming, 18(1), 1–13.
Melliès, P. A. (2017). The parametric continuation monad. Mathematical Structures in Computer Science, 27(5), 651–683.
Michaelis, J. (2001). On formal properties of minimalist grammars. Ph.D. thesis, Universität Potsdam.
Moggi, E. (1991). Notions of computation and monads. Information and Computation, 93(1), 55–92.
Montague, R. (1973). The proper treatment of quantification in ordinary English. In J. Hintikka, J. Moravcsik, & P. Suppes (Eds.), Approaches to natural language (pp. 221–242). Dordrecht: D. Reidel.
Parigot, M. (1992). \(\lambda \mu \)-calculus: An algorithmic interpretation of classical natural deduction. In A. Voronkov (Ed.), Logic programming and automated reasoning, lecture notes in computer science (Vol. 624, pp. 190–201). Berlin: Springer.
Paterson, R. (2012). Constructing applicative functors. In J. Gibbons & P. Nogueira (Eds.), Mathematics of program construction, lecture notes in computer science (Vol. 7342, pp. 300–323). Berlin: Springer.
Pollard, C. (2011). Covert movement in logical grammar. In S. Pogodalla, M. Quatrini, & C. Retoré (Eds.), Logic and grammar: Essays dedicated to Alain Lecomte on the occasion of his 60th birthday, lecture notes in artificial intelligence (Vol. 6700, pp. 17–40). Berlin: Springer.
Seki, H., Matsumura, T., Fujii, M., & Kasami, T. (1991). On multiple context-free grammars. Theoretical Computer Science, 88, 191–229.
Stabler, E. P. (1997). Derivational minimalism. In C. Retoré (Ed.), Logical aspects of computational linguistics, lecture notes in computer science (Vol. 1328, pp. 68–95). Berlin: Springer.
Stabler, E. P., & Keenan, E. L. (2003). Structural similarity within and among languages. Theoretical Computer Science, 293, 345–363.
Vijay-Shanker, K., Weir, D., & Joshi, A. (1987). Characterizing structural descriptions produced by various grammatical formalisms. In Proceedings of the 25th meeting of the association for computational linguistics (pp. 104–111).
Acknowledgements
My thanks to Chris Barker, Dylan Bumford, Simon Charlow, Itamar Francez, Philippe de Groote, and Carl Pollard for their feedback.
Author information
Authors and Affiliations
Corresponding author
Proofs
Proofs
The purpose of this section is to provide a proof of Theorem 3, that graded applicative functors are closed under composition.Footnote 22 It is helpful to first prove a lemma that, for any applicative functor  ,
,  distributes over composition.
distributes over composition.
Lemma 1
If  is a graded applicative functor, then for any \(p \in P\), \(g : \beta \rightarrow \gamma \) and \(f : \alpha \rightarrow \beta \),
is a graded applicative functor, then for any \(p \in P\), \(g : \beta \rightarrow \gamma \) and \(f : \alpha \rightarrow \beta \), 
Proof

\(\square \)
Theorem 3 is repeated below.
Theorem 7
Let \(\mathbf {P}\) be a monoid, and let  be graded applicative functors. Then \(\bigcirc \) is a graded applicative functor, where
be graded applicative functors. Then \(\bigcirc \) is a graded applicative functor, where  , with
, with

The following lemma identifies a useful equality.
Lemma 2

Proof

\(\square \)
Proof
(Proof of Theorem 3) Note first that  , and that
, and that  , as can be seen by inspection of the definitions.
, as can be seen by inspection of the definitions.
identity

composition

homomorphism

interchange

\(\square \)
Rights and permissions
About this article
Cite this article
Kobele, G.M. The Cooper Storage Idiom. J of Log Lang and Inf 27, 95–131 (2018). https://doi.org/10.1007/s10849-017-9263-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-017-9263-1





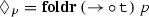 , and
, and  , where
, where  .
. (there called
(there called  (there written as a binary infix operator
(there written as a binary infix operator  and known as
and known as  is familiar as the K axiom, and viewing it as a possibility operator, the type of
is familiar as the K axiom, and viewing it as a possibility operator, the type of 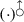 is the axiom T. Lax logic (Fairtlough and Mendler
is the axiom T. Lax logic (Fairtlough and Mendler  and that
and that 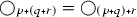 . This is automatic if P is in fact a monoid, but would also be satisfied if, for example,
. This is automatic if P is in fact a monoid, but would also be satisfied if, for example,  is the empty tuple—the monoidal unit for the product operation).
is the empty tuple—the monoidal unit for the product operation).
 , to put the entire expression of type
, to put the entire expression of type  into the store (Kobele
into the store (Kobele  . (The given
. (The given  would correspond to
would correspond to  .) While such a generalization is logically possible, it is problematic in the sense that there is no obvious way for the other elements in the store to bind what should intuitively be their arguments, which have been abstracted over in the newly stored expression.
.) While such a generalization is logically possible, it is problematic in the sense that there is no obvious way for the other elements in the store to bind what should intuitively be their arguments, which have been abstracted over in the newly stored expression. is a forest of unranked trees. For
is a forest of unranked trees. For  ,
,