Skip to main content
SpringerLink
Log in

Fractional Conway Polynomials for Image Denoising with Regularized Fractional Power Parameters

  • Published:
Journal of Mathematical Imaging and Vision Aims and scope Submit manuscript

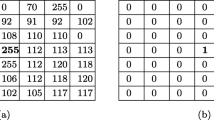
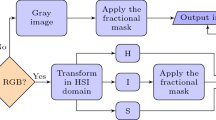
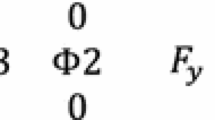Abstract

Image denoising is a significant image processing problem that is difficult to study. The use of fractional masks based on fractional calculus (integral and differential) operators has increased for image denoising. This paper proposes an image denoising algorithm that is based on the generalization of fractional Conway polynomials with regularized fractional power parameters. We operate the structures of fractional masks (differential and integral) by using \(n \times n\) processing masks on eight directions. The performance of the proposed algorithm is evaluated on the basis of visual perception and peak signal-to-noise ratio (PSNR). Theoretical analysis and experimental results demonstrate that the improvements achieved according to visual perception and PSNR values are comparable with Gaussian and Wiener filters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Podlubny, I.: Equations, Fractional Differential, vol. 198 of Mathematics in Science and Engineering, vol. 198. Academic Press, San Diego, CA (1999)

    Google Scholar 

  2. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North Holland Mathematics Studies. Elsevier, Holland (2006)

    MATH  Google Scholar 

  3. Sabatier, J., Agrawal, O.P., Machado, J.T.: Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering. Springer, London (2007)

    Book  Google Scholar 

  4. Lakshmikantham, V., Leela, S.: A Krasnoselskii–Krein-type uniqueness result for fractional differential equations. Nonlinear Anal. 71(7), 3421–3424 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  5. Jalab, H.A., Ibrahim, R.W.: Texture enhancement based on the Savitzky–Golay fractional differential operator. Math. Probl. Eng. 2013, 1–8 (2013)

    MathSciNet  Google Scholar 

  6. Jalab, H.A., Ibrahim, R.W.: Texture enhancement for medical images based on fractional differential masks. Discrete Dyn. Nat. Soc. 2013(2013), 1–10 (2013)

    Google Scholar 

  7. Jalab, H.A., Ibrahim, R.W.: Texture feature extraction based on fractional mask convolution with Cesáro means for content-based image retrieval. In: PRICAI 2012: Trends in Artificial Intelligence, pp. 170–179. Springer, Heidelberg (2012)

  8. Hu, J., Pu, Y., Zhou, J.: A novel image denoising algorithm based on Riemann–Liouville definition. J. Comput. 6(7), 1332–1338 (2011)

    Google Scholar 

  9. Jalab, H.A., Ibrahim, R.W.: Denoising algorithm based on generalized fractional integral operator with two parameters. Discrete Dyn. Nat. Soc. 2012, 1–14 (2012)

  10. Hu, J., Pu, Y., Zhou, J.: Fractional integral denoising algorithm and implementation of fractional integral filter. J. Comput. Inform. Syst. 7(3), 729–736 (2011)

    Google Scholar 

  11. Pu, Y.-F., Zhou, J.-L., Yuan, X.: Fractional differential mask: a fractional differential-based approach for multiscale texture enhancement. IEEE Trans. Image Process. 19(2), 491–511 (2010)

    Article  MathSciNet  Google Scholar 

  12. Guo, H., et al.: Image denoising using fractional integral. In: 2012 IEEE International Conference on Computer Science and Automation Engineering (CSAE). IEEE, Beijing (2012)

  13. Duits, R., et al.: On the axioms of scale space theory. J. Math. Imaging Vis. 20(3), 267–298 (2004)

    Article  MathSciNet  Google Scholar 

  14. Kimmel, R., Sochen, N., Weickert, J.: Scale space and PDE methods in computer vision: 5th International Conference, Scale-Space 2005, Hofgeismar, Germany, April 7–9, 2005, Proceedings, Vol. 3459. Springer, Berlin (2005)

  15. Mathieu, B., et al.: Fractional differentiation for edge detection. Signal Process. 83(11), 2421–2432 (2003)

    Article  MATH  Google Scholar 

  16. Didas, S., et al.: Regularity and scale-space properties of fractional high order linear filtering. In: Scale Space and PDE Methods in Computer Vision, pp. 13–25. Springer, Berlin (2005)

  17. Buades, A., Coll, B., Morel, J.-M.: A review of image denoising algorithms, with a new one. Multiscale Model. Simul. 4(2), 490–530 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  18. Cuesta, E., Kirane, M., Malik, S.A.: Image structure preserving denoising using generalized fractional time integrals. Signal Process. 92(2), 553–563 (2012)

    Article  Google Scholar 

  19. McAndrew, A.: An Introduction to Digital Image Processing with Matlab Notes for SCM2511 Image Processing, pp. 1–264. School of Computer Science and Mathematics, Victoria University of Technology (2004)

  20. Gao, C., et al.: Image enhancement based on improved fractional differentiation. J. Comput. Inform. Syst. 7(1), 257–264 (2011)

    Google Scholar 

  21. Wang, J., et al.: Fractional zero-phase filtering based on the Riemann–Liouville integral. Signal Process. 98, 150–157 (2014)

    Article  Google Scholar 

  22. Qian, K.: Image Processing and Pattern Recognition by Polynomial Approach. ETD collection for University of Nebraska–Lincoln, p. AAI9023021 (1989)

  23. Jassim, W., Raveendran, P., Mukundan, R.: New orthogonal polynomials for speech signal and image processing. Signal Process. IET 6(8), 713–723 (2012)

    Article  MathSciNet  Google Scholar 

  24. Glumov, N.I., Myasnikov, V.V., Sergeyev, V.V.: Application of polynomial bases for image processing using sliding window. In: Digital Image Processing and Computer Graphics: Fifth International Workshop. International Society for Optics and Photonics (1995)

  25. Livingston, C.: Knot Theory, vol. 24. Cambridge University Press, Cambridge (1993)

    MATH  Google Scholar 

  26. Podlubny, I.: Geometric and physical interpretation of fractional integration and fractional differentiation. arXiv: math/0110241 (2001)

  27. Tavassoli, M., Tavassoli, A., Rahimi, M.: The geometric and physical interpretation of fractional order derivatives of polynomial functions. Differ. Geom. Dyn. Syst. 15, 93–104 (2013)

    MathSciNet  Google Scholar 

  28. Zhang, Y.-S., et al.: Fractional domain varying-order differential denoising method. Opt. Eng. 53(10), 102102 (2014). doi:10.1117/1.OE.53.10.102102

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the reviewers for their comments. This research has been funded by university of Malaya, HIR Project UM.C/625/1/HIR/132.

Conflict of interest

The authors declare that they have no competing interests.

Author information

Authors and Affiliations

  1. Faculty of Computer Science and Information Technology, University of Malaya, 50603, Kuala Lumpur, Malaysia

    Hamid A. Jalab

  2. Institute of Mathematical Sciences, University of Malaya, 50603, Kuala Lumpur, Malaysia

    Rabha W. Ibrahim

Authors
  1. Hamid A. Jalab
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rabha W. Ibrahim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hamid A. Jalab.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jalab, H.A., Ibrahim, R.W. Fractional Conway Polynomials for Image Denoising with Regularized Fractional Power Parameters. J Math Imaging Vis 51, 442–450 (2015). https://doi.org/10.1007/s10851-014-0534-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10851-014-0534-z

Keywords

Mathematics Subject Classification

Search

Navigation