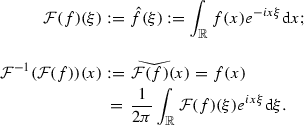On the Mathematical Foundations of Computational Photography

Abstract

Flutter shutter (coded exposure) cameras allow to extend indefinitely the exposure time for uniform motion blurs. Recently, Tendero et al. (SIAM J Imaging Sci 6(2):813–847, 2013) proved that for a fixed known velocity v the gain of a flutter shutter in terms of root means square error (RMSE) cannot exceeds a 1.1717 factor compared to an optimal snapshot. The aforementioned bound is optimal in the sense that this 1.1717 factor can be attained. However, this disheartening bound is in direct contradiction with the recent results by Cossairt et al. (IEEE Trans Image Process 22(2), 447–458, 2013). Our first goal in this paper is to resolve mathematically this discrepancy. An interesting question was raised by the authors of reference (IEEE Trans Image Process 22(2), 447–458, 2013). They state that the “gain for computational imaging is significant only when the average signal level J is considerably smaller than the read noise variance $\sigma _r^2$” (Cossairt et al., IEEE Trans Image Process 22(2), 447–458, 2013, p. 5). In other words, according to Cossairt et al. (IEEE Trans Image Process 22(2), 447–458, 2013) a flutter shutter would be more efficient when used in low light conditions e.g., indoor scenes or at night. Our second goal is to prove that this statement is based on an incomplete camera model and that a complete mathematical model disproves it. To do so we propose a general flutter shutter camera model that includes photonic, thermal (The amplifier noise may also be mentioned as another source of background noise, which can be included w.l.o.g. in the thermal noise) and additive [The additive (sensor readout) noise may contain other components such as reset noise and quantization noise. We include them w.l.o.g. in the readout.] (sensor readout, quantification) noises of finite variances. Our analysis provides exact formulae for the mean square error of the final deconvolved image. It also allows us to confirm that the gain in terms of RMSE of any flutter shutter camera is bounded from above by 1.1776 when compared to an optimal snapshot. The bound is uniform with respect to the observation conditions and applies for any fixed known velocity. Incidentally, the proposed formalism and its consequences also apply to e.g., the Levin et al. motion-invariant photography (ACM Trans Graphics (TOG), 27(3):71:1–71:9, 2008; Method and apparatus for motion invariant imag- ing, October 1 2009. US Patent 20,090,244,300, 2009) and variant (Cho et al. Motion blur removal with orthogonal parabolic exposures, 2010). In short, we bring mathematical proofs to the effect of contradicting the claims of Cossairt et al. (IEEE Trans Image Process 22(2), 447–458, 2013). Lastly, this paper permits to point out the kind of optimization needed if one wants to turn the flutter shutter into a useful imaging tool.

Appendices

Annex 1: Proof of Lemma 1

For any $x \in \mathbb {R}$, we have

$$\begin{aligned} \nonumber&\sum _{n=-\infty }^\infty \left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u\right) (n)\gamma (x-n) \nonumber \\&\quad = \int _{-\infty }^{+\infty }\left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u\right) (y)\gamma (x-y)\mathrm{d}y\end{aligned}$$

(44)

$$\begin{aligned}&\quad =\left[ \left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u\right) *\gamma \right] (x)\end{aligned}$$

(45)

$$\begin{aligned} \nonumber&\quad =\mathcal {F}^{-1}\left[ \mathcal {F}\left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u\right) (\xi ) \mathcal {F}(\gamma )(\xi )\right] (x)\nonumber \\&\quad =\mathcal {F}^{-1}\left[ \hat{\alpha }(\xi v)\hat{u}(\xi ) \hat{\gamma }(\xi )\right] (x)\end{aligned}$$

(46)

$$\begin{aligned}&\quad =\frac{1}{2\pi }\int _{-\infty }^{+\infty }\hat{\alpha }(\xi v) \hat{u}(\xi )\hat{\gamma }(\xi )e^{ix\xi }\mathrm{d}\xi \end{aligned}$$

(47)

$$\begin{aligned}&\quad =\frac{1}{2\pi }\int _{-\pi }^{+\pi }\hat{\alpha }(\xi v) \hat{u}(\xi )\hat{\gamma }(\xi )e^{ix\xi }\mathrm{d}\xi \end{aligned}$$

(48)

$$\begin{aligned}&\quad =\frac{1}{2\pi }\int _{-\pi }^{\pi } \hat{u}(\xi )e^{ix\xi }\mathrm{d}\xi = u(x). \end{aligned}$$

(49)

Poisson’s formula (xxv) justifies (44). Indeed, consider

$$\begin{aligned} f_x(y)=\left[ \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u\right] (y)\gamma (x-y). \end{aligned}$$

(50)

From Cauchy–Schwartz’s inequality we have

$$\begin{aligned} \Vert f_x\Vert _{L^1(\mathbb {R})} \leqslant \left\| \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u \right\| _{L^2(\mathbb {R})} \Vert \gamma \Vert _{L^2(\mathbb {R})}. \end{aligned}$$

Indeed, since $u \in L^1(\mathbb {R})$ by Young’s inequality we have

$$\begin{aligned} \left\| \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u \right\| _{L^2(\mathbb {R})}\leqslant & {} \left\| \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) \right\| _{L^2(\mathbb {R})} \Vert u \Vert _{L^1(\mathbb {R})}\\= & {} \Vert \alpha \Vert _{L^2(\mathbb {R})} \Vert u \Vert _{L^1(\mathbb {R})} < + \infty , \end{aligned}$$

because $\alpha \in L^2(\mathbb {R})$ and $u \in L^1(\mathbb {R})$. Since $\gamma \in L^2(\mathbb {R})$, from (50), we deduce that $f_x \in L^1(\mathbb {R})$. Moreover, we have

$$\begin{aligned} \hat{f}_x(\xi )=\left( \left( \hat{\alpha }\left( \cdot v\right) \hat{u}\left( \cdot \right) \right) *\hat{\gamma }\left( \cdot \right) e^{-ix\xi }\right) (\xi ). \end{aligned}$$

(51)

Since u is $[-\pi ,\pi ]$ band-limited and $\gamma$ is $[-\pi ,\pi ]$ band-limited from its Definition (19) we deduce that $\hat{f}_x(\xi )=0$ for all $\xi \in \mathbb {R}$ such that $|\xi |>\pi$. Yet, from Poisson’s formula (xxv) this only implies that

$$\begin{aligned} \sum _n f_x(n)=\hat{f}_x(0)+\hat{f}_x(-2\pi )+\hat{f}_x(2\pi ). \end{aligned}$$

From (51), $f_x(y)$ is given by a convolution. Thus,

$$\begin{aligned} \hat{f}_x(2\pi )= & {} \int _\mathbb {R}\hat{\alpha }(\xi v) \hat{u}(\xi )\hat{\gamma }(\xi -2\pi )e^{-ix\xi }\mathrm{d}\xi \\= & {} \int _{-\pi }^\pi \hat{\alpha }(\xi v) \hat{u}(\xi )\hat{\gamma }(\xi -2\pi )e^{-ix\xi }\mathrm{d}\xi \end{aligned}$$

since $\hat{u}$ is $[-\pi ,\pi ]$ band-limited. Since the integrand is non-zero on the set $\{\pi \}$, which has Lebesgue measure zero, we deduce that $\hat{f}_x(2\pi )=0$. Similarly we obtain $\hat{f}_x( -2\pi )=0$. The validity of (45)–(46) is, from the continuity of the $L^2(\mathbb {R})$ function $\mathbb {R}\ni x \mapsto \left[ \left( \frac{1}{|v|}\alpha \left( \frac{\cdot }{v}\right) *u\right) *\gamma \right] (x)$, obvious. Not less obvious is (47) from the inverse Fourier transform definition (xxiii). The definition (19) of $\hat{\gamma }$ justifies (48). The fact that u is $[-\pi ,\pi ]$ band-limited and again the definition of $\hat{\gamma }$ (19) justifies (49) and completes our proof.

Annex 2: Proof of Lemma 2

We first prove (23) then prove that $\mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,ana}(\cdot ) \right)$ can be written as the sum of an $L^1(\mathbb {R})$ function and a constant. From Proposition 3, for any $x\in \mathbb {R}$, we have

$$\begin{aligned} \mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,ana}(x) \right) =\sum _{n=-\infty }^\infty \mathrm {var}\left( obs(n)\right) (\gamma (x-n))^2. \end{aligned}$$

(52)

Therefore, combining Proposition 1 (Eq. (7)) and (52), for any $x\in \mathbb {R}$, we have

$$\begin{aligned} \nonumber&\mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,ana}(x) \right) \\ \nonumber&\quad =\sum _{n=-\infty }^\infty \left[ \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (n)\right. \nonumber \\&\qquad \left. + \left( \Vert \alpha \Vert _{L^1(\mathbb {R})} \left( \mu +\sigma _o^2\right) +\sigma ^2_r\right) \right] \left( \gamma (x-n)\right) ^2 \nonumber \\&\quad =\sum _{n=-\infty }^\infty \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (n)(\gamma (x-n))^2 \nonumber \\&\qquad +\left( \Vert \alpha \Vert _{L^1(\mathbb {R})} \left( \mu +\sigma _o^2\right) +\sigma ^2_r\right) \sum _{n=-\infty }^\infty (\gamma (x-n))^2 \end{aligned}$$

(53)

$$\begin{aligned}&\quad =\sum _{n=-\infty }^\infty \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (n)(\gamma (x-n))^2 \\ \nonumber&\qquad +\,\Vert \gamma \Vert _{L^2(\mathbb {R})}^2\left( \Vert \alpha \Vert _{L^1(\mathbb {R})} \left( \mu +\sigma _o^2\right) +\sigma ^2_r\right) , \end{aligned}$$

(54)

and (23) is proved. As a consequence, the function $\mathbb {R}\ni x \mapsto \mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,ana}(x) \right)$ can be written as

$$\begin{aligned} \mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,ana}(x) \right)= & {} f_{\text {ana}}(x) +\Vert \gamma \Vert _{L^2(\mathbb {R})}^2\\&\times \left( \Vert \alpha \Vert _{L^1(\mathbb {R})} \left( \mu +\sigma _o^2\right) +\sigma ^2_r\right) , \end{aligned}$$

where $f_{\text {ana}}(\cdot )$ is defined by (24). It remains to justify that $f_{\text {ana}} \in L^1(\mathbb {R})$. We have

$$\begin{aligned}&\int _{-\infty }^{+\infty } \left| \sum _{n=-\infty }^\infty \left[ \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (n)(\gamma (x-n))^2\right] \right| \mathrm{d}x\\&\quad \leqslant \int _{-\infty }^{+\infty }\sum _{n=-\infty }^\infty \left[ \left| \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (n)\right| (\gamma (x-n))^2 \right] \mathrm{d}x\\&\quad =\sum _{n=-\infty }^\infty \left[ \left| \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (n)\right| \int _{-\infty }^{+\infty }(\gamma (x-n))^2dx \right] \\&\quad =\sum _{n=-\infty }^\infty \left[ \left| \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (n)\right| \Vert \gamma \Vert _{L^2(\mathbb {R})}^2 \right] \\&\quad =\Vert \gamma \Vert _{L^2(\mathbb {R})}^2 \sum _{n=-\infty }^\infty \left| \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (n)\right| \\&\quad =\Vert \gamma \Vert _{L^2(\mathbb {R})}^2 \int _{-\infty }^{+\infty } \left| \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u\right) (x)\right| \mathrm{d}x\\&\hbox { (by~(xxv) equation~(57))}\\&\quad = \Vert \gamma \Vert _{L^2(\mathbb {R})} \left\| \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u \right\| _{L^1(\mathbb {R})}<\\&\qquad +\infty (L^1 *L^1 \subset L^1 \hbox { convolution)}. \end{aligned}$$

This concludes our proof.

Annex 3: Proof of Proposition 4

We first prove (26) then (27). From the numerical flutter shutter samples definition (Definition 6), since, by assumption, $\mathbb {E}(\eta (n))=0$ we have

$$\begin{aligned} \mathbb {E}\left( obs(n) \right)= & {} \sum _{k=0}^{L-1} \alpha _k \int _{k \Delta t}^{(k+1)\Delta t} u(n-vt)+\mu +\sigma _o^2 \mathrm{d}t\\= & {} \int _0^{L\Delta t} \alpha (t) \left( u(n-v t)+\mu +\sigma _o^2\right) \mathrm{d}t . \end{aligned}$$

Thus,

$$\begin{aligned} \nonumber \mathbb {E}\left( obs(n) \right)= & {} \int _0^{L|v|\Delta t} \frac{1}{|v|} \alpha \left( \frac{t}{v}\right) \left( u(n-t)+\mu +\sigma _o^2 \right) \mathrm{d}t\\= & {} \left( \frac{1}{|v|} \alpha \left( \frac{\cdot }{v}\right) *u \right) (n)+\left( \mu + \sigma _o^2\right) \left( \int _{-\infty }^\infty \alpha (t) \mathrm{d}t \right) \end{aligned}$$

and (26) is proved. We now prove (27). From Definition 6, since $\mathrm {var}\left( \eta (n) \right) =\sigma ^2_r$ we have

$$\begin{aligned}&\mathrm {var}\left( obs(n) \right) \\&\quad = \sum _{k=0}^{L-1} \alpha _k^2 \left( \int _{k\Delta t}^{(k+1)\Delta t} u(n-vt)+\mu +\sigma _o^2 dt+\mathrm {var}\left( \eta (k) \right) \right) \\&\quad =\left( \frac{1}{|v|} \alpha ^2\left( \frac{\cdot }{v}\right) *\left( u +\mu +\sigma _o^2\right) \right) (n) + \sum _{k=0}^{L-1} \alpha _k^2 \mathrm {var}\left( \eta (k) \right) \\&\quad =\left( \frac{1}{|v|} \alpha ^2\left( \frac{\cdot }{v}\right) *u \right) (n)+ \Vert \alpha \Vert ^2_{L^2(\mathbb {R})} \left( \mu +\sigma _o^2\right) + \sum _{k=0}^{L-1} \alpha _k^2 \sigma _r^2 \\&\quad =\left( \frac{1}{|v|} \alpha ^2\left( \frac{\cdot }{v}\right) *u \right) (n) + \Vert \alpha \Vert _{L^2(\mathbb {R})}^2 \left( \mu +\sigma _o^2\right) + \frac{ \Vert \alpha \Vert _{L^2(\mathbb {R})}^2}{\Delta t}\sigma _r^2 \\&\quad = \left( \frac{1}{|v|} \alpha ^2\left( \frac{\cdot }{v}\right) *u \right) (n) + \Vert \alpha \Vert _{L^2(\mathbb {R})}^2 \left( \mu +\sigma ^2_o + \frac{\sigma _r^2}{\Delta t} \right) \end{aligned}$$

and (27) is proved. This concludes our proof.

Annex 4: Proof of Theorem 2

The proof follows the same path as the proof of Lemma 2 on Annex 1: we first justify that $\mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,num}(x)\right)$ can be written as the sum of an $L^1(\mathbb {R})$ function and a constant. We then prove the formula in Theorem 2.

From Proposition 5, we have that

$$\begin{aligned}&\mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,num}(x) \right) \\&\quad =\sum _{n=-\infty }^\infty \mathrm {var}\left( obs(n) \right) (\gamma (x-n))^2\\&\quad =\sum _{n=-\infty }^\infty \left[ \left( \frac{1}{|v|} \alpha ^2\left( \frac{\cdot }{v}\right) *u\right) (n)+ \Vert \alpha \Vert _{L^2(\mathbb {R})}^2\right. \\&\qquad \left. \left( \frac{\sigma _r^2}{\Delta t} + \mu +\sigma _o^2\right) \right] (\gamma (x-n))^2, \end{aligned}$$

where the last equality is justified by Proposition 4. The rest of the calculation is similar to (53)–(54) in Annex 1, and we obtain that

$$\begin{aligned} \mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,num}(x) \right)= & {} f_{\text {num}}(x)+\Vert \alpha \Vert _{L^2(\mathbb {R})}^2 \Vert \gamma \Vert _{L^2(\mathbb {R})}^2 \\&\times \left( \frac{\sigma _r^2}{\Delta t} + \mu +\sigma _o^2\right) , \end{aligned}$$

for any $x \in \mathbb {R}$, where

$$\begin{aligned} f_{\text {num}}(\cdot )\!:=\! \sum _{n=-\infty }^\infty \left[ \left( \frac{1}{|v|} \alpha ^2\left( \frac{\cdot }{v}\right) *u\right) (n)(\gamma (\cdot -n))^2\right] \!\in \! L^1(\mathbb {R}). \end{aligned}$$

The proof that $f_{\text {num}} \in L^1(\mathbb {R})$ is identical to the proof that $f_{\text {ana}} \in L^1(\mathbb {R})$ given in Annex 1. Indeed, $\alpha \in L^1(\mathbb {R}) \cap L^2(\mathbb {R})$ and therefore $\alpha ^2 \in L^1(\mathbb {R})$. We now justify the formula in Theorem 2. From Proposition 5, for any $x\in \mathbb {R}$ we have $\mathbb {E}({\widetilde{\mathbbm {u}}}_\mathrm{est,num}(x))=\widetilde{u}(x)$ and therefore $\mathbb {E}|{\widetilde{\mathbbm {u}}}_\mathrm{est,num}(x) - \widetilde{u}(x) |^2=\mathrm {var}\left( {\widetilde{\mathbbm {u}}}_\mathrm{est,num}(x) \right) .$ Thus, by similar calculations between Lemma 2 and Theorem 1 we obtain

$$\begin{aligned}&\lim _{T \rightarrow +\infty }\frac{1}{2T} \int _{-T}^T \mathbb {E}|{\widetilde{\mathbbm {u}}}_\mathrm{est,num}(x) - \widetilde{u}(x)|^2 \\&\quad dx= \Vert \alpha \Vert _{L^2(\mathbb {R})}^2 \Vert \gamma \Vert _{L^2(\mathbb {R})}^2 \left( \frac{\sigma _r^2}{\Delta t} + \mu +\sigma _o^2\right) \end{aligned}$$

and Theorem 2 is proved.

Annex 5: Main Notations and Formulae

• (i) t time variable

• (ii) $\Delta t$ length of a time interval (exposure time)

• (iii) $x \in \mathbb {R}$ spatial variable

• (iv) $X \sim Y$ means that the random variables X and Y have the same law

• (v) $\mathbb {P}(A)$ probability of an event A

• (vi) $\mathbb {E}(X)$ expected value of a random variable X

• (vii) $\mathrm {var}(X)$ variance of a random variable X

• (viii) $f *g$ convolution of two $L^2 (\mathbb {R})$ functions $(f *g)(x) = \int _{\mathbb {R}} f(y) g(x-y) dy$ (the validity is discussed as soon as both functions are not in $L^2(\mathbb {R})$)

• (ix) $l(t,x)>0 ~ \forall ~ x \in \mathbb {R}^+ \times \mathbb {R}$ continuous landscape before passing through the optical system

• (x) $\mathcal P(\lambda )$ Poisson random variable with intensity $\lambda >0$

• (xi) $g$ point-spread-function of the optical system. Assumption $g\in S(\mathbb {R})$ ($S(\mathbb {R})$ denotes the Schwartz class on $\mathbb {R}$)

• (xii) $\sigma _o^2<+\infty$ variance of the thermal noise

• (xiii) $\sigma _r^2<+\infty$ variance of the additive (sensor readout, quantization) noise

• (xiv) $\mu <+\infty$ average mean of $\widetilde{u}$ (see (xv))

• (xv) $\widetilde{u}=\mathbbm {1}_{[-\frac{1}{2},\frac{1}{2}]}*g*l$ ideal observable landscape just before sampling. Assumption: $\widetilde{u}$ $[-\pi ,\pi ]$ band-limited, $\mu :=\lim _{T\rightarrow +\infty } \frac{1}{2T} \int _{-T}^T \widetilde{u}(x) \mathrm{d}x$ and $u:=(\widetilde{u}-\mu ) \in L^1(\mathbb {R})\cap L^2(\mathbb {R})$

• (xvi) $obs(n)$, $n \in \mathbb {Z}$ observation of the landscape at pixel n

• (xvii) ${\widetilde{\mathbbm {u}}}_\mathrm{est,ana}$ estimated landscape for the analog flutter shutter from the observed samples $obs(n)$ where $n \in \mathbb {Z}$. It is defined to have $\mathbb {E}({\widetilde{\mathbbm {u}}}_\mathrm{est,ana}(x))=\widetilde{u}(x)$ for any $x \in \mathbb {R}$.

• (xviii) ${\widetilde{\mathbbm {u}}}_\mathrm{est,num}$ estimated landscape for the numerical flutter shutter from the observed samples $obs(n)$ where $n \in \mathbb {Z}$. It is defined to have $\mathbb {E}({\widetilde{\mathbbm {u}}}_\mathrm{est,ana}(x))=\widetilde{u}(x)$ for any $x \in \mathbb {R}$.

• (xix) v relative velocity between the landscape and the camera (unit: pixels per second)

• (xx) $\alpha (t)$ flutter shutter gain function.

• (xxi) $\mathbbm {1}_{[a,b]}$ indicator function of an interval [a, b]

• (xxii) $\Vert f \Vert _{L^1(\mathbb {R})}= \int _\mathbb {R}|f(x)| \mathrm{d}x$, $\Vert f \Vert _{L^2(\mathbb {R})}= \sqrt{\int _\mathbb {R}|f(x)|^2 \mathrm{d}x}$

• (xxiii) Let $f,g \in L^1(\mathbb {R})$ or $L^2(\mathbb {R})$, then

  

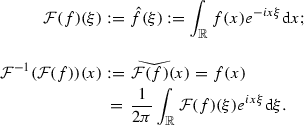
  Moreover $\mathcal {F}(f*g)(\xi )=\mathcal {F}(f)(\xi )\mathcal {F}(g)(\xi )$ and (Plancherel)

  $$\begin{aligned} \int _{\mathbb {R}} |f(x)|^2dx= & {} \Vert f \Vert _{L^2(\mathbb {R})}^2=\frac{1}{2 \pi } \int _{\mathbb {R}} |\mathcal {F}(f)|^2(\xi ) \mathrm{d}\xi \nonumber \\&= \frac{1}{2\pi } \left\| \mathcal {F}(f) \right\| _{L^2(\mathbb {R})}^2. \end{aligned}$$

  (55)

• (xxiv) $\mathrm {sinc}(x)=\frac{\sin (\pi x)}{\pi x}=\frac{1}{2 \pi } \mathcal {F}(\mathbbm {1}_{[-\pi ,\pi ]})(x)=\mathcal {F}^{-1}(\mathbbm {1}_{[-\pi ,\pi ]})(x)$

• (xxv) (Poisson summation formula) Let $\varphi \in L^1(\mathbb {R})$ be $[-\pi ,\pi ]$ band-limited.

  $$\begin{aligned} \sum _n \varphi (n)=\sum _k \hat{\varphi }(2k\pi ). \end{aligned}$$

  (56)

  Since $\varphi$ is $[-\pi ,\pi ]$ band-limited $\hat{\varphi }(\xi )=0$ $\forall \xi \in \mathbb {R}$ such that $|\xi |>\pi$, then from Poisson’s formula (xxv) Eq. (56) we have

  $$\begin{aligned} \sum _n\varphi (n)=\hat{\varphi }(0)=\int _{\mathbb {R}}\varphi (x)\mathrm{d}x. \end{aligned}$$

  (57)

  This applies to any shift of $\varphi$, so we also have

  $$\begin{aligned} \sum _n\varphi (x+n)=\int _{\mathbb {R}}\varphi (x)\mathrm{d}x. \end{aligned}$$

  (58)