Prioritized surgery scheduling in face of surgeon tiredness and fixed off-duty period

Abstract

In this paper, we apply a scheduling model to address the single day surgery scheduling problem for single operating room (OR). The OR operational cost and patients’ satisfaction need to be balanced. We optimize the scheduling of surgeries with two priority levels in an integrated manner, given the OR is off-duty for a fixed period. Surgeon’s accumulated tiredness during working hours, and controllable surgery durations are modeled. After deriving the NP-hardness of the problem, we first solve optimally two special cases in pseudo-polynomial time, and then design a hybrid evolutionary multi-objective algorithm for the general case. Iterated local search is embedded into the elitist non-dominated sorting genetic algorithm (NSGA-II) framework, and Pareto optimal property is utilized to guide evolution towards promising areas in solution space. Finally computational studies with data from a hospital in P.R. China are performed to verify the value of algorithm hybridization against the commercial solver and original NSGA-II, and to verify the value of integrated optimization against sequential decision-making.

1 Introduction

The managerial issue of providing health care services has recently become a hot research topic for several reasons, including aging population trend around the world, rocketing health care cost in developed countries, and mounting complaints about difficulties in getting treated in developing countries (Zhong et al. 2014). The aim of health care management in hospital is two-folded: to lower the operational cost and to maximize patients’ satisfaction. The unit of special interest is the operating room (OR), as a major cost driver as well as a revenue generator involving various stakeholders (Jebali et al. 2006). Effective OR scheduling is of vital importance for successful health care management (Cardoen et al. 2010; Zhong et al. 2014).

Operating room scheduling focuses on the determination of a sequence of surgeries for patients as well as resources assigned to each surgery within each OR in hospital over a day or a week (Jebali et al. 2006). A detailed review of OR planning and scheduling was provided by Cardoen et al. (2010), who summarized 247 manuscripts with almost half appearing in or after 2000. Cardoen et al. (2009a, b) studied the problem of sequencing patients within the ORs of a freestanding ambulatory surgical center in a multi-objective manner. Again in a day-care facility, sequencing of surgical cases was optimized based on a multi-criteria objective function considering the peak use of recovery beds, recovery overtime occurrence, and patient and surgeon preference violations (Cardoen et al. 2009a, b). Column generation was proposed in together with dynamic programming for the pricing problem. Regarding a surgical patient as a job, and the related surgeons and surgical staffs as multiple machines needed, Zhong et al. (2014) studied an OR scheduling model as a machine scheduling problem denoted by $Pm|MMJ|C_{max}$. Since the problem was NP-hard in nature, a two-stage heuristic approach was developed and applied to increase the health management performance in a hospital of Shanghai, P.R. China.

Several practical OR situations have rarely been addressed in the above literature, imposing the rationale of our study. First, patients are usually with various priority levels based on patient-related attributes (health status, difficulty and surgery duration). Surgeries with higher priority should be scheduled ahead of those with lower priority. Second, the surgery planning horizon is assumed to be continuous. The constant off-duty period in the working day (usually between 12:00 pm and 1:00 pm) would make the obtained schedule sub-optimal. Third, the surgery duration is assumed as irrelevant of its starting time in the schedule. Actually the surgeon’s tiredness increases as the operation continues, and later starting of a surgery leads to a longer duration. Besides, the surgery duration is controllable by allocating extra resources. For example, a surgery covers a sequence of activities, such as preincision, incision and postincision (Batun et al. 2011). The durations of preincision or postincision could be shortened by allocating more surgical staffs. Fourth, the OR scheduling problem is usually a NP-hard combinatorial optimization problem with multiple objectives, making exact algorithm intractable as the problem size increases. As a result, meta-heuristics, which could approximate the problem’s Pareto front efficiently (Rahimi-Vahed and Mirghorbani 2007), are required.

The remainder of this paper is organized as follows. In Sect. 2 the OR scheduling problem is formulated, and its intractable complexity is provided. In Sect. 3 two special cases of the problem are solved to optimum. On top of the results and analyzed Pareto optimal property, we design an evolutionary multi-objective algorithm to approximate the optimal Pareto front. The effectiveness of the algorithm is verified through computational studies in Sect. 4. Finally Sect. 5 concludes this paper and points out future research directions.

2 Problem formulation

We focus on the single day surgery scheduling problem for single OR of the surgical center in a hospital. The sequence of elective inpatient surgeries is determined to obtain a qualitative schedule under given constraint. ‘Elective’ means the surgeries are not urgent and could be well planned in advance. A surgical patient is regarded as a job waiting to be processed, and the entire resources within the OR (surgeons, anesthesiologists, nurses and surgical equipments) are consolidated as a single machine. A single day of constant working hours (usually 8 h) with fixed off-duty period, separating the morning/afternoon sessions, is set as the planning period. A group of high-priority patients and a group of low-priority patients are considered. Assume the available working hours capacity could accommodate all patients. Surgeries of low-priority start only when surgeries of high-priority have been finished.

The set of patients is denoted by $J=\{J_1,\ldots ,J_{n}\}$. Denote $[t_1,t_2]$ by the off-duty period during which surgeries could not be performed, and denote 0 and $L$ by the starting and ending times of working hours respectively. All patients are ready at time 0 after initial hospitalization procedure for pre-surgical health status examination. Let $Pr_i \in \{1,2\}$ denote $J_i$’s priority $(1\le i \le n)$. ‘1’ means higher priority than ‘2’. Assume that the estimated surgery duration of patient $J_i$ is $\bar{p}_i$. The OR and surgeon turnover times have been included in $\bar{p}_i$ for each patient. As the surgeries continue, the surgeon and surgical staff get tired, which is modeled by assuming that the actual surgery duration $p_i$ is a non-decreasing function of its starting time $t_i$: $p_i=\bar{p}_i+\alpha \cdot t_i$ (Ji et al. 2013; Yu 2014; He and Sun 2015), where $\alpha$ is the deterioration rate shared by all patients. After period $[t_1,t_2]$, the duration deterioration is fully restored and restarts all over again. $p_i$ is also controllable by allocating extra resources. Let $u_i$ denote the amount of resource allocated to patient $J_i$, and the surgery duration could be shortened by $b_i u_i$ with an additional cost $c_i u_i$, where $0\le u_i\le \bar{u}_i < \bar{p}_i/b_i$, $b_i$ and $c_i$ are the positive compression rate and the unit resource cost for patient $J_i$, and $\bar{u}_i$ is an upper bound on $u_i$ for patient $J_i$. Thus, $p_i$ could be rewritten as $p_i=\bar{p}_i+\alpha \cdot t_i-b_iu_i$. For any feasible schedule $S$, let $C_i(S)$ denote the completion time of patient $J_i$.

The scheduling problem is to determine the sequence of patients of two priority levels over $[0,t_1]\cup [t_2,L]$, and the resource allocation of each surgery to balance between patients satisfaction and OR operational cost. The quality of a schedule $S$ is measured by two objectives: schedule cost denoted by $C$, i.e., the total completion time, and the resource cost denoted by $V$. Since the schedule cost decreases as the resource allocated to the jobs is increased, we cannot minimize both objectives at the same time. Therefore, we focus on finding the set of all Pareto-optimal schedules (points) $(C,V)$, where a schedule $S$ with $C=C(S)$ and $V=V(S)$ is called Pareto-optimal(or efficient) if there does not exist another schedule $S'$ such that $C(S')\le C(S)$ and $V(S')\le V(S)$ with at least one of these inequalities being strict. By the classic 3-field notation in machine scheduling, we could formulate our problem as (P): $1|\bar{p}_i+\alpha t_i-u_i,nr-a|( \sum _{i=1}^{n} C_i, \sum _{i=1}^{n} c_iu_i)$, where ‘$nr-a$’ denotes the off-duty period (Lee and Lin 2001). Without confusion, $C_i(S)$ is abbreviated as $C_i$. Without $\alpha$, $u_{i}$ or patient priorities, problem (P) could be reduced to the single machine flowtime scheduling with unavailability constraint, which has been proved to be NP-hard (Adiri et al. 1989; Kacem et al. 2013). Therefore problem (P) is also NP-hard, and is not polynomially solvable until P = NP.

3 Solution procedure

We present the Pareto optimal property of problem (P) in Theorem 1. Based on the property, we design a pseudo-polynomial time dynamic programming algorithm to optimally solve two special cases: maximum and zero resource allocation for each surgery. For the general case where arbitrary resource allocation is considered, we introduce iterated local search (ILS) into the classic elitist non-dominated sorting genetic algorithm (NSGA-II, Deb et al. 2002) framework. This hybridization is supported by the complementary relationship between ILS and NSGA-II. NSGA-II, with its wide applicability in optimization, suffers from getting trapped in local optimum, especially for large-size problems. An effective way to handle this problem is to strike a balance between exploitation and exploration (Crepinsek et al. 2013). ILS, a generally applicable random search method with simplicity, has produced state-of-the-art performance in the scheduling literature (Pan and Ruiz 2012). Its effectiveness and efficiency have been recognized (Jaradat et al. 2014). Using ILS to exploit around current good solutions and using NSGA-II to explore unknown solution space are expected to produce good results. The enhanced NSGA-II with ILS is abbreviated as NSGA-II/ILS. On top of NSGA-II/ILS, we make use of Pareto-optimal property and population initialization based on solutions to special cases to further enhance the performance.

Theorem 1

For fixed job processing times, i.e., given resource allocation strategy, there exists an optimal schedule for problem (P) in which the jobs of the same priority finish no later than $t_1$ and begin their processing at time $t_2$ are scheduled according to non-increasing order of $\overline{p}_j-b_ju_j$, respectively.

Proof

The proof is straightforward by the pairwise exchange technique. $\square$

3.1 Special cases of maximum or zero resource allocation

Since problem (P) is NP-hard, we handle this by firstly solving its two special cases to optimum by a pseudo-polynomial algorithm. We focus on two special cases: the resource allocations of all jobs are either maximum or zero. Solutions to two special cases would be used in designing meta-heuristics for the general case where job’s resource allocation is arbitrary.

Let $J^1$ and $J^2$ be the sets of jobs with higher and lower priorities respectively, and $|J^1|=n_1$, $|J^2|=n_2$, $n_1+n_2=n$. Here we do not consider the trivial situation where two groups of surgeries could be arranged before $t_1$. Let $T^{(l)}=\sum _{j=1}^{n_1}p^{(l)}_{[j]}(1+\alpha )^{n_1-j}$, where $l\in \{1,2\}$, superscript $l=1$ denotes the case that $u_j=\overline{u}_j$ while superscript $l=2$ denotes the case that $u_j=0$, i.e., $p^{(1)}_{[j]}=\overline{p}_{[j]}-b_j\overline{u}_j$ and $p^{(2)}_{[j]}=\overline{p}_{[j]}$, $[j]$ is the subscript of the job scheduled in the $j\hbox {th}$ position and $p^{(l)}_{[1]} \le p^{(l)}_{[2]} \le \cdots \le p^{(l)}_{[n_1]}$. If $T^{(l)}\ge t_1$, by Theorem 1, the following algorithm would be implemented on $J^1$, otherwise on $J^2$. The only difference between two cases is the start processing time. For $T^{(l)} \ge t_1$, DP starts from zero for the job set $J^1$, otherwise DP starts from $T^{(l)}$ for the job set $J^2$. We illustrate the procedure for $T^{(l)}< t_1$, and the idea is the same for other case.

Arrange the jobs in $J^2$ in the SPT order such that $p^{(l)}_{[n_1+1]}\le p^{(l)}_{[n_1+2]}\le \cdots \le p^{(l)}_{[n_1+n_2]}$. Let $(i,x,y,f^{(l)})$ be a state for a feasible sub-schedule for jobs $J_{[n_1+1]}$, $J_{[n_1+2]}$, $\ldots$, $J_{[n_1+i]}$ such that the total processing time for the jobs before $t_1$ is $x$, the total processing time for the jobs after $t_2$ is $y$, and the corresponding objective value of the sub-schedule is $f^{(l)}$. Let ${\mathcal {S}}_{i}^{(l)}$ be the set that contains the states for all generated sub-schedules for jobs $J_{[n_1+1]}, J_{[n_1+2]},\ldots , J_{[n_1+i]}$. Our algorithm will use Theorem 1 to solve the problem by determining the whole set of non-eliminated states. This is done by dynamically updating the set ${\mathcal {S}}_{i}^{(l)}$ from ${\mathcal {S}}_{i-1}^{(l)}$ for $i=1,\ldots ,n_2$. The algorithm is initialized by setting ${\mathcal {S}}_{0}^{(l)}= \{(0, 0, 0,0)\}$. For each $(i-1,x,y,f^{(l)})\in {\mathcal {S}}_{i-1}^{(l)}$, to schedule job $J_{[n_1+i]}$, there are two cases to consider.

Case 1 job $J_{[n_1+i]}$ can be completed prior to $t_1$, i.e., $p^{(l)}_{[n_1+i]}+(1+\alpha )(T^{(l)}+x)\le t_1$, and add state $(i,x+p^{(l)}_{[n_1+i]} +\alpha (T^{(l)}+x),y,f^{(l)}+p^{(l)}_{[n_1+i]} +(1+\alpha )(T^{(l)}+x))$ to ${\mathcal {S}}_{i}^{(l)}$.

Case 2 job $J_{[n_1+i]}$ is the last job after $t_2$, and its completion time is $t_2+p^{(l)}_{[n_1+i]}+(1+\alpha )y$, and thus add state $(i,x,p^{(l)}_{[n_1+i]}+(1+\alpha )y,f^{(l)}+t_2+p^{(l)}_{[n_1+i]} +(1+\alpha )y)$ to ${\mathcal {S}}_{i}^{(l)}$. In summary, the algorithm is stated in Fig. 1.

Fig. 1

Framework of dynamic programming for special cases

Theorem 2

The above algorithm solves two special cases optimally in $O(n_2 (t_1-T^{(l)})P^{(l)}))$ time, where $P^{(l)}=\sum \nolimits _{i=1}^{n_2}p^{(l)}_{[n_1+i]}(1+\alpha )^{n_2-i},\quad l=1,2$.

Proof

The correctness comes from the above analysis and Theorem 1. For the time complexity, in each iteration $i$, the total number of possible states $(i,x,y,f^{(l)})$ can be calculated in the following way: there are at most $t_1-T^{(l)}$ possible values for $x$, at most $P^{(l)}$ possible values for $y$. Because of the elimination rules, the total number of different states in ${\mathcal {S}}_{i}^{(l)}$ is determined by the different combination of possible values for $x$ and $y$, and hence the total number of possible states in ${\mathcal {S}}_{i}^{(l)}$ is $O((t_1-T^{(l)})P^{(l)})$. Thus, after $n_2$ iterations, Step 3 can be executed in $O(n_2 (t_1-T^{(l)})P^{(l)})$ time, as required. $\square$

Thus, for the case that $T^{(l)}< t_1$, applying the above algorithm, we can obtain two extreme points of the Pareto front, say $(f^{(1)*},\sum c_j\overline{u}_j)$ and $(f^{(2)*},0)$.

3.2 General case of arbitrary resource allocation

When arbitrary resource allocation is considered, decisions for high-priority surgeries clearly affect the satisfaction of low-priority patients. By allocating more resources, we could finish high-priority surgeries earlier and improve low-priority patients’ satisfaction. We handle this in an integrated manner by optimizing high-priority and low-priority surgeries together, through a hybridized evolutionary multi-objective optimization algorithm: NSGA-II/ILS. The algorithm’s framework is shown in Fig. 2. We provide the algorithm’s detailed key elements in the remainder of this subsection.

Fig. 2

Framework of NSGA-II/ILS

• (1) Encoding scheme

A $2n$-dimensional vector is used to represent a feasible solution: where $i=1,2,\ldots ,pop$, and $t=1,2,\ldots ,N$. $pop$ stands for population size, and $N$ is the maximum generation number. $i$ means the $i\hbox {th}$ individual, and $t$ means the $t\hbox {th}$ generation.

The first $n$ entries of are a sequence permutation of $n$ surgeries. The $(n+i)$th $(1\le i \le n)$ entry stands for the resource allocation percentage for the surgery in the $i$th position. The sub-vector of the first $n$ entries is denoted as $\pi$-part, and the sub-vector of the last $n$ entries is denoted as $y$-part.

• (2) Population initialization

To initialize the population, firstly two optimal solutions to special cases with maximum and zero resource allocations are used as initial individuals to guide the search towards promising area in solution space. Secondly, the rest $pop-2$ individuals are randomly generated from given distribution to ensure solution diversity. For each individual, its $\pi$-part is a randomly generated $n$-dimensional sequence, and its $y$-part consists of random numbers subject to uniform distribution $U[0,1]$.

• (3) Fitness evaluation and non-dominated sorting

For each individual, by arranging patients with higher priority before those with lower priority while keeping SPT order for each priority class (surgeries before $t_1$ and after $t_2$ follow SPT order respectively), a schedule specifying operation sequence and resource allocation could be obtained. For the solutions violating capacity constraint, they are penalized by adding an extremely large positive constant to their fitness values, in favor of those feasible solutions.

Then we could calculate the two objective values for each individual, and perform the non-dominated sorting procedure. The entire population is divided into $K$ ranks $\{F_1,F_2,\ldots ,F_K\}$. Given two ranks $F_i$ and $F_j$, $i<j$ means each solution in $F_j$ is dominated by certain solution in $F_i$. For each individual in the same rank, a crowding distance is calculated to measure its distance to its neighbors, reflecting solution diversity. Finally fitness is assigned for each individual. Individuals with lower rank are assigned higher fitness value, and individual with larger crowding distance in the same rank is assigned higher fitness. Please refer to Deb et al. (2002) for details.

• (4) Selection and crossover operation

For the current population, the tournament selection operator is used to organize the mating pool. Then the intermediate crossover is chosen to perform crossover operation. For each entry of two selected individuals, the following procedure is performed with probability $P_c$: $o_{i,j,t} =p_{r1,j,t} + rand \cdot ratio \cdot ( p_{r2,j,t} - p_{r1,j,t} )$, where $i=1,2,\ldots ,pop;j=1,2,\ldots ,2n;t=1,2,\ldots ,N$.

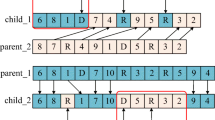
$o_{i,j,t}$ is the $j\hbox {th}$ entry of the $i\hbox {th}$ children individual in $t\hbox {th}$ generation. $p_{r1,j,t}$ and $p_{r2,j,t}$ are the $j\hbox {th}$ entry of the $(r1)\hbox {th}$ and $(r2)\hbox {th}$ parent individuals in the mating pool. $rand$ is a random number subject to uniform distribution $U[0,1]$, and $ratio$ is the crossover coefficient. A repair procedure is needed for an infeasible sequence or resource allocation: for the $\pi$-part, round all numbers to be integers, then replace the repeated indexes with the missing indexes, and make sure high-priority patients precede low-priority patients; for the $y$-part, adjust the values to stay within [0,1].

• (5) Mutation operation

Gaussian mutation is used to adaptively create perturbation for each children individual with probability $P_m$. For the $j\hbox {th}$ entry of the $i\hbox {th}$ children individual in $t\hbox {th}$ generation, we have $o_{i,j,t}=o_{i,j,t}+rand \cdot (scale-shrink \cdot scale \cdot t/N)\cdot (u_{limit,j}-l_{limit,j} )$, where $i=1,2,\ldots ,pop$, $j=n+1,n+2,\ldots ,2n$, and $t=1,2,\ldots ,N$.

$scale$ is the scale of mutation point, $shrink$ is the mutation shrink coefficient, and $u_{limit,j}$ and $l_{limit,j}$ are the upper and lower bounds for $o_{i,j,t}$. $rand$ is uniformly generated from the interval [0,1]. Similar repair procedure with the crossover operation is triggered after mutation if an infeasible solution emerges. The above procedure is for the $y$-part of an individual, and similar procedure is performed on each position of the $\pi$-part. From the mutation formula, the perturbation intensity is large at the beginning to accelerate convergence, and adaptively decreases as evolution continues to avoid destroying obtained high-quality solutions.

• (6) Iterated local search

In order to balance between solution quality and convergence speed, we randomly choose $ILS_{percentage}$ percentage of individuals from current children population to perform ILS on the $\pi$-parts. The $y$-parts are correspondingly adjusted after. The main idea of ILS is to search randomly around local optima in the solution space. Starting from the current individual, ILS operations of local search, perturbation, and acceptance criterion judgement are implemented (Pan and Ruiz 2012; Jaradat et al. 2014). For local search, the insertion move and the exchange move are used for the 2-opt local search operation. The insertion move randomly chooses an entry in the $\pi$-part and inserts it into any position in the sequence. The exchange move randomly chooses two not necessarily adjacent entries and swap their positions. For perturbation, two swap moves and one exchange move are used, and the entire procedure would repeat for $ILS_{iteration}$ times followed by local search. For acceptance criterion judgement, the new optimum is accepted only if it strictly dominates the starting individual. During this process, an initial local optimum continuously goes through perturbation and local search to obtain a new local optimum. We don’t put the locally improved individual back into the population to compete for reproductive opportunities, but only keep the improved fitness value according to Baldwinian learning mechanism (Lim et al. 2010). The improved optimum is recorded in the archive $E$.

4 Computational studies

In order to verify the effectiveness of NSGA-II/ILS, we design computational studies, the data of which come from a survey in the eye department at a large Class-3 Level-A hospital in Liaoning Province, China. One key operating room of the eye department opens from 8:00 AM to 12:00 PM, then is off-duty from 12:00 PM to 1:00 PM so that the surgeon and surgical staff could rest to recover from accumulated tiredness, and opens again from 1:00 PM to 5:00 PM for each working day. The planning horizon for surgeries consists of two separate periods of the same length. On average, 20–30 ocular surgeries (cataract, glaucoma, etc.) are performed. Each surgery usually takes between 10 and 20 min, and its duration could be compressed by allocating more medical resources. In order to guarantee the variety, practical relevance and parsimony properties in experiment design, we generate problem instances as follows.

The total number of surgeries $n$ takes three levels of values: 20, 25 and 30. For each surgery $J_i (1\le i \le n)$, its normal processing time $\overline{p}_i$ is randomly generated from uniform distribution $U[10,20]$, its positive compression rate $b_i$ is from uniform distribution $U[0,1]$, its unit resource cost $c_i$ is from uniform distribution $U[2,9]$, and its priority is also randomly generated as 1 or 2. The deteriorating rate for modeling surgeon tiredness is set as $\alpha =0.01$ through the survey. The working hours begin at zero time index and end at $L=540$. The off-duty period is between $t_1=240$ and $t_2=300$. For each problem size, 10 problem instance are generated and solved by the proposed algorithms for 30 replications. The results are compared for four evolutionary multi-objective algorithms: original NSGA-II without SPT property, NSGA-II/ILS without SPT property, NSGA-II/ILS, and NSGA-II/ILS+DP with two initial individuals from solutions to special cases of problem (P). All algorithms are coded in MATLAB (2012a) and implemented on a PC with 4G RAM, Intel Core i5 CPU 2.5GHz.

4.1 Parameters tuning

Parameters including $pop$, $P_c$, $P_m$, $N$, $ILS_{percentage}$, and $ILS_{iteration}$ clearly affect the algorithm performance. We use the problem instance of $n=20$ for parameter tuning by Design of Experiment methods. It starts from each parameter taking an initial value, focuses on the parameters one by one, and examines the change of minimum distance to the ideal point of the obtained Pareto front as the concerned parameter changes. The tuned parameters would be shared by relevant algorithms. The candidate parameter values and distance values are as follows: $pop\in$ {50 (598.03), 100 (563.59), 150 (565.27)}, $N\in$ {100 (608), 150 (576.30), 200 (568.1), 250 (568.1)}, $ILS_{percentage}\in$ {0.1 (567.02), 0.3 (563.59), 0.5 (565.27)}, $ILS_{iteration} \in$ {1 (569.62), 3 (586.31), 5 (573.82)}, $P_c \in$ $\{1/n$ (566.2), $2/n$ (559.2), $3/n$ (570.4), $4/n$ (588.9)}, $ratio\in$ {0.8 (584.3), 1.2 (570.4), 1.6 (581.5)}, $P_m \in \{1/n$ (570.5), $2/n$ (573.9), $3/n$ (604), $4/n$ (612.4)}, $(scale,shrink) \in$ {(0.1,0.1) (607.2), (0.1,0.5) (606.4), (0.1,0.9) (569.2), (0.5,0.1) (565.2), (0.5,0.5) (568.1), (0.5,0.9) (587.5), (0.9,0.1) (567.4), (0.9,0.5) (567.9), (0.9,0.9) (581.2)}. Parameters with minimum distance value are chosen.

4.2 The value of algorithm hybridization and integrated optimization

For $n=20$, one typical result is shown in Fig. 3a. All evolutionary algorithms terminate within 1 min. In order to verify the algorithm’s performance against benchmark results, we use the Euclidean distance to the ideal point to handle bi-objective in the model, and solve the non-linear MIP program (see Appendix for detail) by commercial solver with maximum running time set as 1 h. The average result (META-SOLVER) / SOLVER of 10 problem instances for each case is shown in Table 1, ‘META’ and ‘SOLVER’ are the minimum distances returned by the meta-heuristic and the solver. We can see that original NSGA-II’s performance is inferior to solver, and with the help of algorithm hybridization and high-quality initial solution, NSGA-II/ILS and its variants outperform commercial solver in both quality and efficiency.

Table 1 Algorithm’s performance against commercial solver (%)

We could make several observations from Fig. 3a. First, if the SPT property with respect to allocated resource is not embedded in the algorithm, the Pareto front’s quality is inferior. By comparing ‘NSGA-II without SPT’ and ‘NSGA-II/ILS without SPT’, we could clearly see that hybridization of local search into NSGA-II framework could decrease the premature probability of NSGA-II, and return a better Pareto front in dominance relationship. Second, by introducing SPT property into NSGA-II/ILS, the obtained Pareto front could be extended along the direction which favors the total completion time. This result could be attributed to Theorem 1 that SPT rule minimizes the total completion time. However, focusing solely on patients satisfaction generates relatively high operational cost for the OR management. This result is usually not acceptable in practise. Third, the solutions returned by NSGA-II/ILS+DP dominate most of the solutions returned by other methods. The uniform spread between two extreme solutions in correspondence to two special cases to problem (P) and the convergence towards true Pareto front directly verify the effectiveness of our proposed approach.

Fig. 3

Pareto fronts of comparative algorithms. a The value of algorithm hybridization. b The value of integrated optimization

We further compare the Pareto fronts obtained by four evolutionary algorithms by use of Pareto front performance indicators: the IGD metric (Zhou et al. 2014) and the $HV$ metric (Lim et al. 2010). The IGD metric measures the average distance of candidate Pareto front to the reference set of optimal Pareto front, reflecting solutions’ convergence. The $HV$ metric measures the area covered by a Pareto front in two-dimensional objective space, reflecting solutions’ convergence and diversity in a comprehensive manner. Smaller IGD values and larger $HV$ values denote better performance. The average (ave) and standard deviation (std) of relative percentage of each concerned algorithm over 30 replications for $n=20,25,30$ is summarized in Table 2, where ‘ave’ means (ave(method 1)$-$ave(method 2))/ave(method 2), and ‘std’ means (std(method 1)$-$std(method 2))/std(method 2). ‘NSGA-II/ILS without SPT’ is against original NSGA-II, ‘NSGA-II/ILS’ is against ‘NSGA-II/ILS without SPT’, and ‘NSGA-II/ILS+DP’ is against ‘NSGA-II/ILS’. Negative IGD percentage and positive $HV$ percentage mean the concerned algorithm outputs high-quality Pareto front in convergence and diversity. From Table 2, each version of NSGA-II/ILS outperforms its corresponding competitor, and the results are more stable from the negative relative std percentage. The performance improvement brought by hybridizing local search into NSGA-II, Pareto optimal property, and solutions to special cases are well demonstrated. The advantage of NSGA-II/ILS becomes more obvious as $n$ increases, indicating our algorithm is more appropriate for single day OR scheduling problem when the number of surgeries is relatively large.

Table 2 Relative performance indicator values (%)

The previous results are all obtained in an integrated optimization manner, and we compare the results of NSGA-II/ILS with those obtained through sequentially optimize high-priority surgeries and then low-priority surgeries. If high-priority surgeries are finished before $t_1$, we solve to optimum the equally-weighted aggregated objective by converting it to an assignment problem according to Vickson (1980), assuming equal weight for the two objectives, and use NSGA-II/ILS to optimize low-priority surgeries over $[T^{(l)},t_1]$ and $[t_2,L]$. Otherwise we apply NSGA-II/ILS first then solve the assignment problem. The result of $n=20$ is shown in Fig. 3b. The value of integrated optimization could directly be illustrated since the integrated manner outputs a Pareto front with better convergence and diversity. What is more, the average relative IGD value of integrated over sequential decision making for $n=20,25,30$ are $-$98.47, $-$97.66, and $-$97.91 %. And the average relative $HV$ value for three cases are 68.81, 77.75, and 80.47 %. To summarize, simultaneously optimizing two groups of patients outperforms sequentially optimizing the high-priority patients first then the low-priority patients.

5 Conclusions

In this study, we utilize a scheduling model to examine the single day surgical scheduling for single OR. A surgery is regarded as a job, and the surgeons, anesthesiologists, nurses and surgical equipments within the OR are consolidated as single machine. Two patient priority levels are considered, and the OR would be off-duty for a fixed period in the working day. Surgeon’s accumulated tiredness is modeled by the deteriorating effect, and the controllable surgery duration is modeled by resource allocation. The surgeries scheduling could be dealt with as a single machine scheduling with non-resumable availability constraint, with job’s controllable and deteriorating processing time. In consideration of the underlying complexities, we first optimally solve two special cases, and then design a meta-heuristic algorithm, which has been verified by comparing with classic NSGA-II and the commercial solver.

Our study could be summarized as follows. In theoretical aspect, we introduce a single machine scheduling model with availability constraint, deteriorating and controllable processing time for the surgery scheduling problem. In algorithmic aspect, we hybridize local search into NSGA-II framework, construct initial population from optimal solutions to special cases of problem, and verify the algorithm’s effectiveness through comparative studies. In application aspect, our model and algorithm lay the foundation for design of automated surgery scheduling system. The current traditional manual scheduling procedure, which is still mainstream in most hospitals in China, would inefficiently produce inferior solutions. In the future, designing and implementing surgery scheduling system, and examining its impact on OR management would be our goal of interest.

Appendix

$$\begin{aligned} \begin{array}{llll} {\min }&{}{ \sqrt{{\Big (\sum \limits _{j = 1}^n {{C_j}}-f^{(1)*}\Big )^2 + \Big (\sum \limits _{j = 1}^n {{c_j}{u_j}}\Big )^2} } }&{} &{}\\ {s.t.}&{}{{s_i} + \alpha ({s_i} - (1 - {y_i}){t_2}) + {{\bar{p}}_i} - {b_i}{u_i} \le {C_i}}&{}{1 \le i \le n}&{}{(1)}\\ &{}{{C_i} \le {s_j} + M(1 - {x_{ij}})}&{}{1 \le i < j \le n;{{\Pr }_i},{{\Pr }_j} = 1}&{}{(2)}\\ &{} &{}{\hbox {or} \quad 1 \le i < j \le n;\,{{\Pr }_i},\,{{\Pr }_j} = 1}&{}\\ &{}{{C_j} \le {s_i} + M{x_{ij}}}&{}{1 \le i < j \le n;\,{{\Pr }_i},\,{{\Pr }_j} = 1}&{}{(3)}\\ &{} &{}\mathrm{or} \quad 1 \le i < j \le n;\,{\Pr }_{i},\,{\Pr }_j = 1 &{}\\ &{}{{C_i} \le {s_j}}&{}{1 \le i,j \le n;\,{{\Pr }_i} = 1,\,{{\Pr }_j} = 2}&{}{(4)}\\ &{}{{C_i} \le {t_1} + M(1 - {y_i})}&{}{1 \le i \le n}&{}{(5)}\\ &{}{{t_2} \le s_i + M{y_i}}&{}{1 \le i \le n}&{}{(6)}\\ &{}{0 \le {u_i} \le {{\bar{u}}_i}}&{}{1 \le i \le n}&{}{(7)}\\ &{}{s_i,{C_i} \ge 0;{y_i} \in \{ 0,1\} }&{}{1 \le i \le n}&{}{(8)}\\ &{}{{x_{ij}} \in \{ 0,1\} }&{}{1 \le i < j \le n;\,{{\Pr }_i},\,{{\Pr }_j} = 1}&{}\\ &{} &{}{\hbox {or} \quad 1 \le i < j \le n;\,{{\Pr }_i},\,{{\Pr }_j} = 1}&{} \end{array} \end{aligned}$$

In the above formulation, $M$ is a very large positive number, and decision variable notations are introduced as follows: $s_i$ is the earliest starting time of job $J_i$, $C_i$ is the completion time of job $J_i$, $u_i$ is the resource allocation for job $J_i$, $x_{ij}$ equals 1 if job $J_i$ is scheduled before job $J_j$ and 0 otherwise, and $y_i$ equals 1 if job $J_i$ is scheduled before $t_1$ and 0 otherwise. $f^{(1)*}$ is the minimum value of schedule performance.