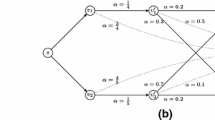
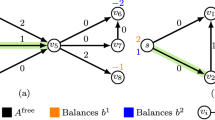
Abstract
We study an extension of the well-known minimum cost flow problem in which a second kind of costs (called usage fees) is associated with each edge. The goal is to minimize the first kind of costs as in traditional minimum cost flows while the total usage fee of a flow must additionally fulfill a budget constraint. We distinguish three variants of computing the usage fees. The continuous case, in which the usage fee incurred on an edge depends linearly on the flow on the edge, can be seen as the \(\varepsilon \)-constraint method applied to the bicriteria minimum cost flow problem. We present the first strongly polynomial-time algorithm for this problem. In the integral case, in which the fees are incurred in integral steps, we show weak \({\mathcal {NP}}\)-hardness of solving and approximating the problem on series-parallel graphs and present a pseudo-polynomial-time algorithm for this graph class. Furthermore, we present a PTAS, an FPTAS, and a polynomial-time algorithm for several special cases on extension-parallel graphs. Finally, we show that the binary case, in which a fixed fee is payed for the usage of each edge independently of the amount of flow (as for fixed cost flows—Hochbaum and Segev in Networks 19(3):291–312, 1989), is strongly \({\mathcal {NP}}\)-hard to solve and we adapt several results from the integral case.





Similar content being viewed by others
Notes
As it is common when dealing with network flow problems, we assume throughout the paper that all of these values are integral, which is no restriction for most of the applications since we can multiply all values with their least common denominator in case of rational data (cf., e.g., Ahuja et al. 1993).
Note that the enhanced capacity scaling algorithm as introduced in Ahuja et al. (1993) is designed for graphs without parallel edges and runs in \({\mathcal {O}}(m \log n (m + n \log n))\) time. Nevertheless, it can be shown that this running time worsens only slightly to the claimed one if we allow parallel edges.
We refer to Ehrgott (2005) for an in-depth treatment of bicriteria optimization problems and efficient solutions.
Note that the values \(A_G(c,b,f)\) computed by our procedure are actually only correct under the additional restriction that the flow is positive only on shortest paths in \(G_y\) for some upgrade profile \(y\). Hence, our procedure may output \(A_G(c,b,f)=+\infty \) in some cases even though the value is actually finite. Nevertheless, by the above argument and since we always minimize over \(c, b\), and \(f\) in each step of the algorithm, we compute \(A_G(c,b,f)\) correctly for each triple of values \(c,b,f\) that correspond to an optimal flow that is positive only on shortest paths for some upgrade profile in a considered component.
We assume that \( \left\lfloor \frac{b}{b_e} \right\rfloor = +\infty \) if \(b_e=0\).
References
Ahuja RK, Magnanti TL, Orlin JB (1993) Network flows. Prentice Hall, Network Flows
Ahuja RK, Orlin JB (1995) A capacity scaling algorithm for the constrained maximum flow problem. Networks 25(2):89–98
Bein WW, Brucker P, Tamir A (1985) Minimum cost flow algorithms for series-parallel networks. Discret Appl Math 10:117–124
Booth H, Tarjan RE (1992) Finding the minimum-cost maximum flow in a series-parallel network. J Algorithms 15:416–446
Burkard RE, Dlaska K, Klinz B (1993) The quickest flow problem. Z für Oper Res 37(1):31–58
Chankong V, Haimes YY (2008) Multiobjective decision making: theory and methodology., Dover books on engineering seriesDover Publications, Incorporated, New York
Demgensky I, Noltemeier H, Wirth HC (2002) On the flow cost lowering problem. Eur J Operat Res 137(2):265–271
Demgensky I, Noltemeier H, Wirth HC (2004) Optimizing cost flows by edge cost and capacity upgrade. J Discret Algorithms 2(4):407–423
Maya Duque PA, Coene S, Goos P, Sörensen K, Spieksma F (2013) The accessibility arc upgrading problem. Eur J Operat Res 224(3):458–465
Ehrgott M (2005) Multicriteria optimization, 2nd edn. Springer, Berlin
Garey MR, Johnson DS (1979) Computers and intractability—a guide to the theory of \({\cal NP}\)-completeness. W.H. Freeman and Company, New York
Geoffrion AM (1967) Solving bicriterion mathematical programs. Operat Res 15(1):39–54
Han Y, Pan V, Reif J (1992) Efficient parallel algorithms for computing all pair shortest paths in directed graphs. In: Proceedings of the fourth annual ACM symposium on Parallel algorithms and architectures, ACM, pp. 353–362
Hochbaum DS, Segev A (1989) Analysis of a flow problem with fixed charges. Networks 19(3):291–312
Kellerer H, Pferschy U, Pisinger D (2004) Knapsack problems. Springer, Berlin
Krumke SO, Schwarz S (1998) On budget-constrained flow improvement. Inf Process Lett 66(6):291–297
Krumke SO, Marathe MV, Noltemeier H, Ravi R, Ravi SS (1998) Approximation algorithms for certain network improvement problems. J Comb Optim 2(3):257–288
Megiddo N (1979) Combinatorial optimization with rational objective functions. Math Operat Res 4(4):414–424
Megiddo N (1983) Applying parallel computation algorithms in the design of serial algorithms. JACM 30(4):852–865
Schrijver A (1998) Theory of linear and integer programming. Wiley, Chichester
Spellman FR (2013) Handbook of water and wastewater treatment plant operations, 3rd edn. Taylor & Francis, Boca Raton
Valdes J, Tarjan RE, Lawler E (1982) The recognition of series parallel digraphs. SIAM J Comput 11:298–313
Acknowledgments
We thank the anonymous referees for their valuable comments and suggestions. Furthermore, we thank Stefan Schwarz for his suggestions on the proof of Theorem 8. This work was partially supported by the German Federal Ministry of Education and Research within the project “SinOptiKom—Cross-sectoral Optimization of Transformation Processes in Municipal Infrastructures in Rural Areas”.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Holzhauser, M., Krumke, S.O. & Thielen, C. Budget-constrained minimum cost flows. J Comb Optim 31, 1720–1745 (2016). https://doi.org/10.1007/s10878-015-9865-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-015-9865-y