A solution to a conjecture on the generalized connectivity of graphs

Abstract

The generalized k-connectivity $\kappa _k(G)$ of a graph G was introduced by Chartrand et al. in (Bull Bombay Math Colloq 2:1–6, 1984), which is a nice generalization of the classical connectivity. Recently, as a natural counterpart, Li et al. proposed the concept of generalized edge-connectivity for a graph. In this paper, we consider the computational complexity of the generalized connectivity and generalized edge-connectivity of a graph. We give a confirmative solution to a conjecture raised by S. Li in Ph.D. Thesis (2012). We also give a polynomial-time algorithm to a problem of generalized k-edge-connectivity.

1 Introduction

All graphs considered in this paper are undirected, finite and simple. We refer to the book (Bondy and Murty 2008) for graph theoretical notation and terminology not described here. The generalized connectivity of a graph G, introduced by Chartrand et al. in (1984), is a natural and nice generalization of the concept of the standard (vertex-)connectivity. For a graph G(V, E) and a set $S\subseteq V(G)$ of at least two vertices, an S-Steiner tree or a Steiner tree connecting S (or simply, an S-tree) is such a subgraph $T(V',E')$ of G that is a tree with $S\subseteq V'$. Two Steiner trees T and $T'$ connecting S are said to be internally disjoint if $E(T)\cap E(T')=\varnothing$ and $V(T)\cap V(T')=S$. For $S\subseteq V(G)$ and $|S|\ge 2$, the generalized local connectivity $\kappa (S)$ is the maximum number of internally disjoint trees connecting S in G. Note that when $|S|=2$ a Steiner tree connecting S is just a path connecting S. For an integer k with $2\le k\le n$, the generalized k-connectivity $\kappa _k(G)$ of G is defined as $\kappa _k(G)= min\{\kappa (S) : S\subseteq V(G) \ and \ |S|=k\}$. Clearly, when $|S|=2$, $\kappa _2(G)$ is nothing new but the connectivity $\kappa (G)$ of G, that is, $\kappa _2(G)=\kappa (G)$, which is the reason why one addresses $\kappa _k(G)$ as the generalized connectivity of G. Set $\kappa _k(G)=0$ when G is disconnected. Results on the generalized connectivity can be found in Chartrand et al. (2010), Li et al. (2012a, b, 2014a), Li and Li (2012), Li et al. (2010), Li and Mao (2014, 2015a, b, c), Okamoto and Zhang (2010).

As a natural counterpart of the generalized connectivity, Li et al. introduced the concept of generalized edge-connectivity in Li et al. (2014b). For $S\subseteq V(G)$ and $|S|\ge 2$, the generalized local edge-connectivity $\lambda (S)$ is the maximum number of edge-disjoint trees connecting S in G. For an integer k with $2\le k\le n$, the generalized k-edge-connectivity $\lambda _k(G)$ of G is then defined as $\lambda _k(G)= min\{\lambda (S) : S\subseteq V(G) \ and \ |S|=k\}$. It is also clear that when $|S|=2$, $\lambda _2(G)$ is nothing new but the standard edge-connectivity $\lambda (G)$ of G, that is, $\lambda _2(G)=\lambda (G)$, which is the reason why we address $\lambda _k(G)$ as the generalized edge-connectivity of G. Also set $\lambda _k(G)=0$ when G is disconnected.

The generalized edge-connectivity is related to an important problem, which is called the Steiner Tree Packing Problem. For a given graph G and $S\subseteq V(G)$, this problem asks to find a set of maximum number of edge-disjoint Steiner trees connecting S in G. One can see that the Steiner Tree Packing Problem studies local properties of graphs, but the generalized edge-connectivity focuses on global properties of graphs. The generalized edge-connectivity and the Steiner Tree Packing Problem have applications in VLSI circuit design, see Grötschel (1997), Grötschel et al. (1996), Jain et al. (2003), Sherwani (1999). In this application, a Steiner tree is needed to share an electronic signal by a set of terminal nodes. Another application, which is our primary focus, arises in the Internet Domain. Imagine that a given graph G represents a network. We choose arbitrary k vertices as nodes. Suppose that one of the nodes in G is a broadcaster, and all the other nodes are either users or routers (also called switches). The broadcaster wants to broadcast as many streams of movies as possible, so that the users have the maximum number of choices. Each stream of movie is broadcasted via a tree connecting all the users and the broadcaster. So, in essence we need to find the maximum number Steiner trees connecting all the users and the broadcaster, namely, we want to get $\lambda (S)$, where S is the set of the k nodes. Clearly, it is a Steiner tree packing problem. Furthermore, if we want to know whether for any k nodes the network G has the above properties, then we need to compute $\lambda _k(G)$ in order to prescribe the reliability and the security of the network.

As we know, for any graph G, we have polynomial-time algorithms to get the connectivity $\kappa (G)$ and the edge-connectivity $\lambda (G)$. A natural question is whether there is a polynomial-time algorithm to get the $\kappa _3(G)$ or $\lambda _3(G)$, or more generally $\kappa _k(G)$ or $\lambda _k(G)$. In Li et al. (2010), the authors described a polynomial-time algorithm to decide whether $\kappa _3(G)\ge \ell$.

Theorem 1.1

(Li et al. 2010) Given a fixed positive integer $\ell$, for any graph G the problem of deciding whether $\kappa _3(G)\ge \ell$ can be solved by a polynomial-time algorithm.

As a continuation of their investigation, S. Li and X. Li later turned their attention to the general $\kappa _k$ and obtained the following results in Li and Li (2012).

Theorem 1.2

(Li and Li 2012) For two fixed positive integers k and $\ell$, given a graph G, a k-subset S of V(G), the problem of deciding whether there are $\ell$ internally disjoint trees connecting S can be solved by a polynomial-time algorithm.

Theorem 1.3

(Li and Li 2012) For any fixed integer $k\ge 4$, given a graph G, a k-subset S of V(G) and an integer $\ell \ (2\le \ell \le n-2)$, deciding whether there are $\ell$ internally disjoint trees connecting S, namely deciding whether $\kappa (S)\ge \ell$, is ${\mathcal {N}}{\mathcal {P}}$-complete.

Theorem 1.4

(Li and Li 2012) For any fixed integer $\ell \ge 2$, given a graph G and a subset S of V(G), deciding whether there are $\ell$ internally disjoint trees connecting S, namely deciding whether $\kappa (S)\ge \ell$, is ${\mathcal {N}}{\mathcal {P}}$-complete.

In Theorem 1.3, for $k=3$ the complexity is yet not known. So, S. Li in her Ph.D. thesis (2012) conjectured that it is ${\mathcal {N}}{\mathcal {P}}$-complete.

Conjecture 1.5

(Li 2012) Given a graph G and a 3-subset S of V(G) and an integer $\ell \ (2\le \ell \le n-2)$, deciding whether there are $\ell$ internally disjoint trees connecting S, namely deciding whether $\kappa (S)\ge \ell$, is ${\mathcal {N}}{\mathcal {P}}$-complete.

In this paper, we will confirm that this conjecture is true.

For the generalized k-edge-connectivity, it is also natural to consider its computational complexity problem: for any two positive integers k and $\ell$, given a k-subset S of V(G), is there a polynomial-time algorithm to determine whether $\lambda (S)\ge \ell$ ?

We will show that, if both k and $\ell$ are fixed integers, there is a polynomial-time algorithm to determine whether $\lambda _k(G)\ge \ell$.

Theorem 1.6

Given two fixed positive integers k and $\ell$, for any graph G the problem of deciding whether $\lambda _k(G)\ge \ell$ can be solved by a polynomial-time algorithm.

The rest of this paper is organized as follows. In next section we give a confirmative solution to Conjectures 1.5. In Sect. 3, we give the proof of Theorem 1.6.

2 Proof of Conjecture 1.5

In this section, we focus on solving Conjectures 1.5. In order to show that this conjecture is correct, we first introduce a basic ${\mathcal {N}}{\mathcal {P}}$-complete problem and a new problem.

3-Dimensional matching (3-DM) Given three sets $U,\ V$ and W with $|U|=|V|=|W|$, and a subset T of $U\times V\times W$, decide whether there is a subset M of T with $|M|=|U|$ such that whenever (u, v, w) and $(u',v',w')$ are distinct triples in M, we have $u\ne u',$ $v\ne v',$ and $w\ne w'$ ?

Problem 1

Given a tripartite graph $G=(V,E)$ with three partitions $(\overline{U},\overline{V},\overline{W})$, and $|\overline{U}|=|\overline{V}|=|\overline{W}|=q$, decide whether there is a partition of V into q disjoint 3-sets $V_1,V_2,\ldots , V_q$ such that every $V_i=\{v_{i_1},v_{i_2},v_{i_3}\}$ satisfies that $v_{i_1}\in \overline{U}$, $v_{i_2}\in \overline{V}$, $v_{i_3}\in \overline{W}$, and $G[V_i]$ is connected ?

By reducing 3-DM to Problem 1, we can get the following result.

Lemma 2.1

Problem 1 is ${\mathcal {N}}{\mathcal {P}}$-complete.

Fig. 1

Graphs for Lemma 2.1

Proof

It is easy to see that Problem 1 is in ${\mathcal {N}}{\mathcal {P}}$ since given a partition of V(G) into q disjoint 3-sets $V_i\ (i=1,2,\ldots , q)$, one can check in polynomial-time that every $V_i=\{v_{i_1},v_{i_2},v_{i_3}\}$ satisfies that $v_{i_1}\in \overline{U}$, $v_{i_2}\in \overline{V}$, $v_{i_3}\in \overline{W}$, and $G[V_i]$ is connected.

We now prove that 3-DM is polynomially reducible to this problem.

Given three sets $U,\ V$ and W with $|U|=|V|=|W|=n$, and a subset T of $U\times V\times W$. Let $T=\{T_1,T_2,\ldots ,T_m\}$. We will construct a tripartite graph $G[\overline{U},\overline{V},\overline{W}]$ with $|\overline{U}|=|\overline{V}|=|\overline{W}|=q$ such that the desired partition exists for G if and only if there is a subset M of T with $|M|=n$ and whenever (u, v, w) and $(u',v',w')$ are distinct triples in M, we have $u\ne u',$ $v\ne v'$ and $w\ne w'$.

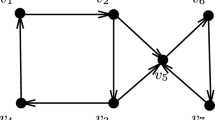
For each $T_i=(u_i,v_i,w_i)$, we add 18 new vertices $V_i^0=\{t_{i_1},t_{i_2},\ldots , t_{i_{18}}\}$ and 26 edges $E_i^0$ which are shown in Fig. 1. Thus $G[\overline{U},\overline{V},\overline{W}]$ is defined by

$$\begin{aligned} \overline{U}= & {} U\bigcup \{t_{i_3},t_{i_6},t_{i_7},t_{i_{10}},t_{i_{13}}, t_{i_{16}}: 1\le i \le m\}\\ \overline{V}= & {} V\bigcup \{t_{i_1},t_{i_4},t_{i_9},t_{i_{12}},t_{i_{14}}, t_{i_{17}}: 1\le i \le m\}\\ \overline{W}= & {} W\bigcup \{t_{i_2},t_{i_5},t_{i_8},t_{i_{11}},t_{i_{15}}, t_{i_{18}}: 1\le i \le m\}\\ V= & {} \overline{U} \cup \overline{V}\cup \overline{W},\ E=\bigcup _{i=1}^{m}E_i^0. \end{aligned}$$

Note that $|V|=3n+18m,$ $|E|=26m$. Thus this instance can be constructed in polynomial-time from a 3-DM instance. Now that $q=n+6m$.

If there is a subset M of T with $|M|=n$, and whenever (u, v, w) and $(u',v',w')$ are distinct triples in M we have $u\ne u',$ $v\ne v',$ and $w\ne w'$, then the corresponding partition $V=V_1\cup V_2\cup \ldots \cup V_q$ is given by taking $\{u_i,t_{i_1},t_{i_2}\}, \{v_i,t_{i_7},t_{i_8}\}, \{w_i,t_{i_{13}},t_{i_{14}}\},\{t_{i_3},t_{i_{4}},t_{i_{5}}\},$ $\{t_{i_9},t_{i_{10}},t_{i_{11}}\},\{t_{i_{15}},$ $t_{i_{16}},t_{i_{17}}\},$ $\{t_{i_6},t_{i_{12}},t_{i_{18}}\}$ from the vertices of $V_i^0\cup T_i$ whenever $T_i=(u_i,v_i,w_i)$ is in M, and by taking $\{t_{i_1},t_{i_2},t_{i_3}\},$ $\{t_{i_4},t_{i_5},t_{i_6}\},\ \{t_{i_7},t_{i_8},t_{i_9}\},$ $\{t_{i_{10}},t_{i_{11}},t_{i_{12}}\},\ \{t_{i_{13}},$ $t_{i_{14}},t_{i_{15}}\},\ \{t_{i_{16}},t_{i_{17}},t_{i_{18}}\}$ from the vertices of $V_i^0$ whenever $T_i=(u_i,v_i,w_i)$ is not in M.

Since $|M|=n$, $|T\backslash M|=m-n$, we can find $7n+6(m-n)=n+6m=q$ partition sets, each set consists of three vertices which belong to $\overline{U},\overline{V},\overline{W},$ respectively, and they induce a connected subgraph.

Conversely, let $V_1, V_2,\ldots , V_q$ be the desired partition of V(G). In the following, we call a 3-set $\{u,v,w\}$ a partition set, if there is some j such that $\{u,v,w\}=V_j$. Then we choose $T_i\in M$ if $\{t_{i_6},t_{i_{12}},t_{i_{18}}\}$ is a partition set.

Now we claim that $|M|=n,$ and whenever (u, v, w) and $(u',v',w')$ are distinct triples in M we have $u\ne u',$ $v\ne v'$ and $w\ne w'$. Indeed, let $T_i=(u_i,v_i,w_i)$. If $\{t_{i_6},t_{i_{12}},t_{i_{18}}\}$ is a partition set, then $\{t_{i_3},t_{i_{4}},t_{i_{5}}\}$ and $\{u_i,t_{i_1},t_{i_2}\}$, or $\{t_{i_2},t_{i_{4}},t_{i_{5}}\}$ and $\{u_i,t_{i_1},t_{i_3}\}$, or $\{t_{i_1},t_{i_3},t_{i_5}\}$ and $\{u_i,t_{i_2},t_{i_4}\}$ are the partition sets. In either cases, $u_i$ must belong to a partition set with the other two elements belong to $V_i^0$. Similar thing is true for $v_i$ and $w_i$. If $\{t_{i_6},t_{i_{12}},t_{i_{18}}\}$ is not a partition set, then $\{t_{i_6},t_{i_{11}},t_{i_{12}}\}$ or $\{t_{i_4},t_{i_5},t_{i_6}\}$ is a partition set. But $\{t_{i_6},t_{i_{11}},t_{i_{12}}\}$ can not be a partition set. If so, then $\{t_{i_8},t_{i_{10}},v_i\}$, $\{t_{i_7},t_{i_8},t_{i_9}\}$ or $\{t_{i_7},t_{i_8},v_i\}$ must be a partition set, and no matter in which cases, $t_{i_9}$ or $t_{i_{10}}$ can not be in a partition set. Thus only $\{t_{i_4},t_{i_5},t_{i_6}\}$ is a partition set. Similarly, $\{t_{i_1},t_{i_2},t_{i_3}\},\ \{t_{i_7},t_{i_8},t_{i_9}\},$ $\{t_{i_{10}},t_{i_{11}},t_{i_{12}}\},\ \{t_{i_{13}},t_{i_{14}},t_{i_{15}}\},\ \{t_{i_{16}},t_{i_{17}},t_{i_{18}}\}$ must be partition sets. Then $u_i,v_i,w_i$ can not be in any partition sets with some vertices in $V_i^0$.

If $T_i=(u_i,v_i,w_i)$ and $T_j=(u_j,v_j,w_j)$ are distinct triples in M, then $u_i$ is in a partition set with the other two elements in $V_i^0$, and $u_j$ is in a partition set with the other two elements in $V_j^0$, and thus $u_i\ne u_j$, and so do $v_i\ne v_j$ and $w_i\ne w_j$. Assume that $|M|=\ell$. If $T_i\in M$, then there are 7 partition sets in $V_i^0\cup T_i$. If $T_i\notin M$, then there are 6 partition sets in $V_i^0$. Since $7\ell +6(m-\ell )=q=n+6m$, $\ell =n$, that is $|M|=n$. The proof is now complete. $\square$

Now we prove that Conjecture 1.5 is true by reducing Problem 1 to it.

Theorem 2.2

Given a graph G, a 3-subset S of V(G) and an integer $\ell$ $(2\le \ell \le n-2)$, the problem of deciding whether G contains $\ell$ internally disjoint trees connecting S is ${\mathcal {N}}{\mathcal {P}}$-complete.

Proof

It is easy to see that this problem is in ${\mathcal {N}}\mathcal {P}$.

Let G be a tripartite graph with partition $(\overline{U},\overline{V},\overline{W})$ and $|\overline{U}|=|\overline{V}|=|\overline{W}|=q$. We will construct a graph $G'$, and a 3-subset S and an integer $\ell$ such that there are $\ell$ internally disjoint trees connecting S in $G'$ if and only if G contains a partition of V(G) into q disjoint sets $V_1,V_2,\ldots , V_q$ each having three vertices, such that every $V_i=\{v_{i_1},v_{i_2},v_{i_3}\}$ satisfies that $v_{i_1}\in \overline{U}$, $v_{i_2}\in \overline{V}$, $v_{i_3}\in \overline{W}$, and $G[V_i]$ is connected.

We define $G'$ as follows:

• $V(G')=V(G)\cup \{a,b,c\}$;

• $E(G')=E(G)\cup \{au:u\in \overline{U}\}\cup \{bv:v\in \overline{V}\}\cup \{cw:w\in \overline{W}\}$.

Then we define $S=\{a,b,c\}$, and $\ell =q$.

If there are q internally disjoint trees connecting S in $G'$, then, since a, b and c all have degree q, each tree contains a vertex from $\overline{U}$, a vertex from $\overline{V}$ and a vertex from $\overline{W}$, and they induce a connected subgraph. Since these q trees are internally disjoint, they form a partition of V(G).

Conversely, if $V_1,V_2, \ldots , V_q$ is a partition of V(G) each having three vertices, such that every $V_i=\{v_{i_1},v_{i_2},v_{i_3}\}$ satisfies that $v_{i_1}\in \overline{U}$, $v_{i_2}\in \overline{V}$, $v_{i_3}\in \overline{W}$, and $G[V_i]$ is connected, then let $T_i$ be the spanning tree of $G[V_i]$ together with the edges $av_{i_1}, bv_{i_2},cv_{i_3}$, where $V_i=\{v_{i_1},v_{i_2},v_{i_3}\}$. It is easy to check that $T_1,T_2,\ldots ,T_q$ are the desired internally disjoint trees connecting S.

This completes the proof. $\square$

3 Proof of Theorem 1.6

In this section we give a proof of Theorem 1.6.

Proof

Given a connected graph G of order n and a k-subset S of V(G). Let $V(G)=\{v_1,v_2,\ldots ,v_n\}$ and $E(G)=\{e_1,e_2,\ldots ,e_m\}$. We will construct a graph $G'$ and a k-subset $S'$ of $V(G')$ such that there are $\ell$ edge-disjoint trees connecting S in G if and only if there are $\ell$ internally disjoint trees connecting $S'$ in $G'$.

We define $G'$ as follows:

• $V(G')=V(G)\cup V(L(G))=\{v_1,v_2,\ldots ,v_n,e_1,e_2,\ldots ,e_m\}$;

• $E(G')=\{e_ie_j:e_ie_j\in E(L(G))\}\cup \{v_ie_j:e_j~is~incident~to~v_i~in~G\}$;

where L(G) is the line graph of G. We define $S'=S$.

If there are $\ell$ edge-disjoint trees connecting S in G, say $T_1,T_2,\ldots ,T_{\ell }$. First for each tree $T_i \ (1\le i\le \ell )$, we replace every edge $e_j=v_{j_1}v_{j_2}$ by a path $v_{j_1}e_jv_{j_2}$. The obtained graph $T_i'$ now is a tree in $G'$. Clearly, the trees $T_1',T_2',\ldots ,T_{\ell }'$ are $\ell$ edge-disjoint trees connecting $S'=S$ in $G'$. Consider the tree $T_i'$. If there is a vertex $v\in V(T_i)\backslash S$ such that its neighbors in $T_i'$ are $e_{i_1},e_{i_2},\ldots ,e_{i_p}$, then we delete the vertex v and its incident edges $ve_{i_1},ve_{i_2},\ldots ,ve_{i_p}$, add a path $e_{i_1}e_{i_2}\ldots e_{i_p}$. We do this operation for all the vertex $v\in V(T_i)\backslash S$ for $1\le i\le \ell$. The resulting trees are denoted by $T_1'',T_2'',\ldots , T_{\ell }''$. It is easy to check that they are internally disjoint trees connecting $S'$ in $G'$.

Conversely, if there are $\ell$ internally disjoint trees $T_1,T_2,\ldots ,T_{\ell }$ connecting $S'$ in $G'$. Consider any tree $T_i \ (1\le i\le \ell )$. If there is an edge $e_{j_1}e_{j_2}$ in $E(T_i)$, by the definition of $E(G')$, $e_{j_1}$ and $e_{j_2}$ are adjacent in G and hence they have a common vertex $v_j$ in G. Note that $v_je_{j_1}, v_je_{j_2}$ are also edges of $G'$. Thus we replace the edge $e_{j_1}e_{j_2}$ by a path $e_{j_1}v_je_{j_2}$. We do this for all the edges of this type in $T_i$. The resulting connected graph is denoted by $G_i$. Now there is no such edge $e_ie_j$ in $G_i$ and $d_{G_i}(e) \le 2.$ If $d_{G_i}(e) = 1,$ we just delete it. If $d_{G_i}(e) = 2,$ there are two vertices $v_{j_1}$ and $v_{j_2}$ adjacent with e, where $v_{j_1}$ and $v_{j_2}$ are the endpoints of e in G, so we delete the vertex e and add an edge $v_{j_1}v_{j_2}$, then the obtained graph $G_i'$ is a connected graph with $S \subseteq V(G_i')$ . Let $T_i'$ be the spanning tree of $G_i'$. It is easy to check that $T_1',T_2',\ldots , T_{\ell }'$ are $\ell$ edge-disjoint trees connecting S in G.

From the above reduction, if we want to know whether there are $\ell$ edge-disjoint trees connecting S in G, we can construct a graph $G'$, and decide whether there are $\ell$ internally disjoint trees connecting $S'$ in $G'$. By Theorem 1.2, since k and $\ell$ are fixed, the problem of deciding whether there are $\ell$ internally disjoint trees connecting S can be solved by a polynomial-time algorithm. Therefore, the problem of deciding whether there are $\ell$ edge-disjoint trees connecting S can be solved by a polynomial-time algorithm. Since $\lambda _k(G)= min\{\lambda (S) : S\subseteq V(G) \ and \ |S|=k\}$, we need to check $n \atopwithdelims ()k$ subsets S of V(G). And because k is fixed, the problem of deciding whether $\lambda _k(G)\ge \ell$ can be solved by a polynomial-time algorithm. The proof is complete. $\square$

4 Concluding remarks

In this paper, we give a confirmative solution to a conjecture raised by S. Li in her Ph.D. thesis. We also consider the computational complexity problem of generalized k-edge-connectivity: for any two positive integers k and $\ell$, given a k-subset S of V(G), is there a polynomial-time algorithm to determine whether $\lambda (S)\ge \ell$ ?

We show that, if both k and $\ell$ are fixed integers, there is a polynomial-time algorithm to determine whether $\lambda _k(G)\ge \ell$. But when k or $\ell$ is not a fixed integer, the complexity of this problem is not known. We conjecture that it is ${\mathcal {N}}{\mathcal {P}}$-complete.

Conjecture 4.1

For any fixed integer $k\ge 3$, given a graph G, a k-subset S of V(G), and an integer $\ell \ (2\le \ell \le n-2)$, deciding whether there are $\ell$ edge-disjoint trees connecting S, namely deciding whether $\lambda (S)\ge \ell$, is ${\mathcal {N}}{\mathcal {P}}$-complete.

Conjecture 4.2

For any fixed integer $\ell \ge 2$, given a graph G, a subset S of V(G), deciding whether there are $\ell$ edge-disjoint trees connecting S, namely deciding whether $\lambda (S)\ge \ell$, is ${\mathcal {N}}{\mathcal {P}}$-complete.