2-Distance coloring of planar graphs with girth 5

Abstract

A vertex coloring is said to be 2-distance if any two distinct vertices of distance at most 2 receive different colors. Let G be a planar graph with girth at least 5. In this paper, we prove that G admits a 2-distance coloring with at most $\Delta (G)+3$ colors if $\Delta (G)\ge 339$.

Appendix: The proofs of the case that v is of type P7 or P8

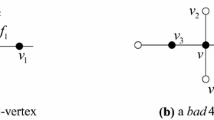
Suppose that v is of type P7 (i.e., $d(v)=4$, $n_2^l(v)=2$ and $n_2^h(v)=1$). Let $N(v)=\{x,y,z,u\}$ in clockwise order with $d(x)=d(y)=d(z)=2$. By Lemma 2.3(8), $d(u)\ge \Delta$. Let $x_1,y_1$ and $z_1$ be the other neighbor of x, y and z, and let $f_1,f_2,f_3$ and $f_4$ be the faces with yvx, zvy, uvz and xvu in their boundaries, respectively. If $d(f_i)\ge 6$ for some $1\le i\le 4$, then $ch(f_i\rightarrow v)\ge \frac{1}{2}$ since $n_b(f_i)\le d(f_i)-2$. Hence, $w^*(v)\ge w^\prime (v)+\frac{1}{2}\ge 0$. Otherwise, we suppose that $d(f_i)=5$ for all $1\le i\le 4$. Let $f_1=[yvxx_1y_1]$, $f_2=[zvyy_1z_1]$, $f_3=[uvzz_1u_1]$ and $f_4=[xvuu_2x_1]$.

We have two possibilities.

Case P71 y is the heavy 2-neighbor of v. It follows that $d(y_1)\ge \Delta -1$. If $d(x_1)\ge 10$, then $x_1y_1$ is a heavy edge, and $ch(x_1\rightarrow f_1)\ge 1$ and $ch(y_1\rightarrow f_1)\ge \frac{3-\varepsilon }{2}$ by $R_{21}$, which imply $ch(f_1\rightarrow v)\ge 1+\frac{3-\varepsilon }{2}$ (as $n_b(f_1)=1$), and so $w^*(v)\ge w'(v)+1+\frac{3-\varepsilon }{2}\ge 0$. Otherwise, we suppose that $3\le d(x_1), d(z_1)\le 9$ by symmetry. By Lemma 2.2, both $x_1$ and $z_1$ have $p^+$-neighbors. With the similar reason, we also suppose that $\max \{d(u_1), d(u_2)\}\le 9$.

Let us calculate $ch(\{f_1, f_2, f_3, f_4\}\rightarrow v)$.

If $d(x_1)\ge 5$, then $w'(x_1)\ge 3d(x_1)-10+3-\varepsilon -(1+\varepsilon )-2(d(x_1)-2)\ge d(x_1)-4-2\varepsilon$ by $R_{11}$ and $R_{15}$ (noticing that $u_2$ is heavy if $d(u_2)=2$), which implies $ch(x_1\rightarrow f_1)\ge \frac{1-2\varepsilon }{5}$. So, $ch(\{f_1, f_2, f_3, f_4\}\rightarrow v)\ge \frac{1-2\varepsilon }{5}$ (as $n_b(f_4)=1$), and $w^*(v)\ge -2\varepsilon +\frac{1-2\varepsilon }{5}\ge 0$. Suppose so that $d(x_1)\le 4$.

If $d(x_1)=3$, then $d(u_2)\ge 3$ by Lemma 2.3(3), and $u_2$ is not a 3(1)-vertex with $n_2^l(u_2)=1$ by Lemma 2.6(1). Now, after the first discharging procedure, $w'(u_2)\ge -1+3-\varepsilon -(1+\varepsilon )-\varepsilon \ge 1-3\varepsilon$ if $d(u_2)=3$ (by $R_{11}$-$R_{13}$ and $R_{15}$), $w'(u_2)\ge 3d(u_2)-10+3-\varepsilon -2(d(u_2)-2)-\varepsilon \ge d(u_2)-3-2\varepsilon$ (by $R_{11}$, $R_{14}$ and $R_{15}$) whenever $d(u_2)\ge 4$. Hence $ch(u_2\rightarrow f_4)\ge \frac{1-2\varepsilon }{4}$, which implies $ch(\{f_1, f_2, f_3, f_4\}\rightarrow v)\ge \frac{1-2\varepsilon }{4}$ (since $n_b(f_4)=1$), and so $w^*(v)\ge -2\varepsilon +\frac{1-2\varepsilon }{4}\ge 0$.

Finally, we suppose that $d(x_1)=4$. By Lemma 2.3(8), $u_2$ is not a light 2-vertex. Therefore, $x_1$ is not a 4-vertex with $n_2^l(x_1)=2$ and $n_2^h(x_1)=1$ by Lemma 2.6(2), and $w'(x_1)\ge 2+3-\varepsilon -4-\varepsilon \ge 1-2\varepsilon$ whenever $n_2^l(x_1)$=2 (noticing that $x_1$ transfers at most $\varepsilon$ to $u_2$ in this situation) or $w'(x_1)\ge 2+3-\varepsilon -2-2(1+\varepsilon )\ge 1-3\varepsilon$ whenever $n_2^l(x_1)\le 1$. It follows that $ch(x_1\rightarrow f_1)\ge \frac{1-3\varepsilon }{4}$, and $ch(f_1\rightarrow v)\ge \frac{1-3\varepsilon }{4}$ ($n_b(f_1)=1$), and so $w^*(v)\ge -2\varepsilon +\frac{1-3\varepsilon }{4}\ge 0$.

Case P72 x is the heavy 2-neighbor of v. It follows that $d(x_1)\ge p$. If $d(u_2)\ge 10$, then $u_2x_1$ and $uu_2$ are both heavy edges, and $f_4$ receives at least $2+3-\varepsilon$ by $R_{21}$, and so $w^*(v)\ge -2\varepsilon +5-\varepsilon \ge 0$. Otherwise, we have $d(u_2)\le 9$. It is easy to check that $w'(u_2)\ge 3d(u_2)-10+2(3-\varepsilon )-2(d(u_2)-2)\ge d(u_2)-2\varepsilon$ since $u_2$ receives at least $3-\varepsilon$ from u and $x_1$, respectively. By $R_{22}$, $ch(u_2\rightarrow f_4)\ge \frac{2-2\varepsilon }{2}$. Hence by $R_{23}$, $w^*(v)\ge -2\varepsilon +ch( f_4\rightarrow v)\ge -2\varepsilon +\frac{2-2\varepsilon }{2}\ge 0$ since $n_b(f_4)=1$.

Suppose that v is of type P8 (i.e., v is a 4-vertex with $n_2^l(v)=3$). Let $N(v)=\{x,y,z,u\}$ with x, y, z being light 2-vertices. By Lemma 2.3(8), $d(u)\ge \Delta$. For convenience, let $x_1,y_1$ and $z_1$ be the other neighbor of x, y and z, respectively. By the definition of light 2-vertex, max $\{d(x_1),d(y_1),d(z_1)\}\le \Delta -2$. For convenience, we assume that $f_1,f_2,f_3$ and $f_4$ are the four faces incident with v, bounded by yvx, zvy, uvz and xvu, respectively. If v is incident with at least two $6^+$-faces, then by Claim 3.4 and $R_{23}$, $w^*(v)\ge -1-\varepsilon +\frac{2}{3}+\frac{1}{2}\ge 0$ or $w^*(v)\ge -1-\varepsilon +\frac{1}{2}\times 3\ge 0$. So we assume that v is incident with at most one $6^+$-face. We have three possibilities.

Case P81 $d(f_2)\ge 6$. Let $f_1=[yvxx_1y_1]$, $f_3=[uvzz_1u_1]$ and $f_4=[xvuu_2x_1]$ with $u_1,u_2\in N(u)$. We will calculate $ch(\{f_1, f_2, f_3, f_4\}\rightarrow v)$. Notice that $ch(f_2\rightarrow v)\ge \frac{2}{3}$ by Claim 3.4.

If $d(x_1)\ge 10$, then $w^\prime (u_2)\ge 3d(u_2)-10+2+3-\varepsilon -2(d(u_2)-2)\ge d(u_2)-1-\varepsilon$ since $u_2$ receives at least 2 from $x_1$ and receives $3-\varepsilon$ from u. By $R_{22}$, $ch(u_2\rightarrow f_4)\ge \frac{1-\varepsilon }{2}$ and $ch(f_4\rightarrow v)\ge \frac{1-\varepsilon }{2}$ since $n_b(f_4)=1$. Hence, we have $w^*(v)\ge -1-\varepsilon +\frac{2}{3}+\frac{1-\varepsilon }{2}\ge 0$.

Otherwise, we may assume that $3\le d(x_1)\le 9$. By Lemma 2.2, $x_1$ is adjacent to a $p^+$-vertex. We claim that $d(y_1)\le p-1$. ( Otherwise, $w'(y)\ge -4+2+3-\varepsilon \ge 1-\varepsilon$ by $R_{11}$ and $R_{15}$ in the first step. By $R_{22}$, $ch(y\rightarrow v)\ge 1-\varepsilon$. Hence, $w^*(v)\ge -1-\varepsilon +\frac{2}{3}+1-\varepsilon \ge 0$.) If $d(u_2)\ge 10$, then $uu_2$ is a heavy edge. By $R_{21}$, $ch(u\rightarrow f_4)\ge \frac{3-\varepsilon }{2}$ and $ch(u_2\rightarrow f_4)\ge 1$. We have $ch(f_4\rightarrow v)\ge \frac{3-\varepsilon }{4}+\frac{1}{2}$ since $n_b(f_4)\le 2$. It follows that $w^*(v)\ge -1-\varepsilon +\frac{2}{3}+\frac{3-\varepsilon }{4}+\frac{1}{2}\ge 0$. Otherwise, we assume that $2\le d(u_2)\le 9$.

If $d(u_2)=2$, then by Lemma 2.3(4), $d(x_1)\ge 4$. If $d(x_1)=4$, $w^\prime (x_1)\ge 2+3-\varepsilon -2-2(1+\varepsilon )\ge 1-3\varepsilon$ by Lemma 2.3(8). If $d(x_1)\ge 5$, then $w^\prime (x_1)\ge 3d(x_1)-10+3-\varepsilon -(1+\varepsilon )-2(d(x_1)-2)\ge d(x_1)-4-2\varepsilon$ since $x_1$ receives at least $3-\varepsilon$ from its $p^+$-neighbors and transfers at most $1+\varepsilon$ to $u_2$. We have $ch(x_1\rightarrow \{f_1, f_4\})\ge \frac{1-2\varepsilon }{5}\times 2$. Hence, $ch(\{f_1, f_4\}\rightarrow v)\ge \frac{1-2\varepsilon }{5}\times 2$ since $n_b(f_1)=1$ and $n_b(f_4)=1$. By $R_{23}$, $w^*(v)\ge -1-\varepsilon +\frac{2}{3}+\frac{1-2\varepsilon }{5}\times 2\ge 0$.

Finally, we assume that $d(u_2)\ge 3$. If $d(x_1)\ge 4$, then $w^\prime (x_1)\ge 3d(x_1)-10+3-\varepsilon -2(d(x_1)-2)-\varepsilon \ge d(x_1)-3-2\varepsilon$ since $x_1$ receives at least $3-\varepsilon$ from its $p^+$-neighbors and transfers at most $\varepsilon$ to $u_2$. We have $ch(x_1\rightarrow \{f_1, f_4\})\ge \frac{1-2\varepsilon }{2}$. Hence $ch(\{f_1, f_4\}\rightarrow v)\ge \frac{1-2\varepsilon }{2}$ since $n_b(f_1)=1$ and $n_b(f_4)=1$. $w^*(v)\ge -1-\varepsilon +\frac{2}{3}+\frac{1-2\varepsilon }{2}\ge 0$. Otherwise, if $d(x_1)=3$, then $d(u_2)\ge 5$ by Lemma 2.7. We have $w^\prime (u_2)\ge 3d(u_2)-10+3-\varepsilon -\varepsilon -2(d(u_2)-2)\ge d(u_2)-3-2\varepsilon$ since $u_2$ receives at least $3-\varepsilon$ from u and transfers at most $\varepsilon$ to $x_1$. Hence, $ch(u_2\rightarrow f_4)\ge \frac{2-2\varepsilon }{5}$. It follows that $w^*(v)\ge -1-\varepsilon +\frac{2}{3}+\frac{2-2\varepsilon }{5}\ge 0$.

Case P82 $d(f_3)\ge 6$. For convenience, let $f_1=[yvxx_1y_1]$, $f_2=[zvyy_1z_1]$ and $f_4=[x_1xvuu_1]$ be the three 5-faces incident with v. By Claim 3.4 and $R_{23}$, $ch(f_3\rightarrow v)\ge \frac{2}{3}$. We consider $ch(u_2\rightarrow f_4)$ and $ch(x_1\rightarrow \{f_1, f_4\})$. This case is quite similar to that of Case P81, so we omit it.

Case P83 $d(f_i)=5$ for all $1\le i\le 4$. Without loss of generality, let $f_1=[yvxx_1y_1]$, $f_2=[zvyy_1z_1]$, $f_3=[uvzz_1u_1]$ and $f_4=[xvuu_2x_1]$ with $u_1,u_2\in N(u)$. If $d(u_2)\ge 10$, then $uu_2$ is a heavy edge, $ch(\{u,u_2\}\rightarrow f_4)\ge 1+\frac{3-\varepsilon }{2}$ and $ch(f_4\rightarrow v)\ge \frac{1}{2}+\frac{3-\varepsilon }{4}$ since $n_b(f_4)\le 2$. It follows that $w^*(v)\ge -1-\varepsilon +\frac{1}{2}+\frac{3-\varepsilon }{4}\ge 0$.

So we may assume that $2\le d(u_1)\le 9$ and $2\le d(u_2)\le 9$ by symmetry. In the following, we will calculate the charge transferred from $x_1,z_1,y_1,u_1,u_2$ to $f_1,f_2,f_3$ and $f_4$.

Subcase P831 $d(x_1)\ge 10$ and $d(z_1)\ge 10$. If $d(y_1)\ge 10$, then both $x_1y_1$ and $y_1z_1$ are heavy edges. Hence, $ch(\{x_1,y_1,z_1\}\rightarrow \{f_1, f_2\})\ge 4$. It follows that $w^*(v)\ge -1-\varepsilon +4\ge 0$ since $n_b(f_1)=n_b(f_2)=1$. Otherwise, we may assume that $3\le d(y_1)\le 9$. By Lemma 2.2, $y_1$ is adjacent to at least one $p^+$-vertex. It is easy to calculate that $w^\prime (u_2)\ge 3d(u_2)-10+2+3-\varepsilon -2(d(u_2)-2)\ge d(u_2)-1-\varepsilon$ by $R_{11}$ and $R_{15}$. By $R_{22}$, $ch(u_2\rightarrow f_4)\ge \frac{1-\varepsilon }{2}$ and $ch(f_4\rightarrow v)\ge \frac{1-\varepsilon }{2}$ since $n_b(f_4)=1$. By symmetry, $ch(f_3\rightarrow v)\ge \frac{1-\varepsilon }{2}$.

Moreover, by $R_{11}$ and $R_{15}$, $w^\prime (y_1)\ge 3d(y_1)-10+4-2(d(y_1)-2))\ge d(y_1)-2$, which shows that $ch(y_1\rightarrow \{f_1, f_2\})\ge \frac{2}{3}$. Again, since $n_b(f_1)=n_b(f_2)=1$, $ch(\{f_1,f_2\}\rightarrow v)\ge \frac{2}{3}$. Totally, $ch(\{f_1, f_2, f_3, f_4\}\rightarrow v)\ge \frac{1-\varepsilon }{2}+\frac{1-\varepsilon }{2}+\frac{2}{3}$. It follows that $w^*(v)\ge -1-\varepsilon +(1-\varepsilon )+\frac{2}{3}\ge 0$.

Subcase P832 $d(x_1)\ge 10$ and $d(z_1)\le 9$. Similar to that of above, if $d(y_1)\ge 10$, then $x_1y_1$ is a heavy edge. Hence, $ch(\{x_1,y_1\}\rightarrow f_1)\ge 2$. It follows that $w^*(v)\ge -1-\varepsilon +2\ge 0$ since $n_b(f_1)=1$. Otherwise, we may assume that $3\le d(y_1)\le 9$.

If $10\le d(x_1)\le p-1$, then $d(y_1)\ge 4$ and $y_1$ is adjacent to a $p^+$-vertex by Lemma 2.2. It is easy to check that $w^\prime (y_1)\ge 3d(y_1)-10+2+3-\varepsilon -\varepsilon -2(d(y_1)-3))\ge d(y_1)+1-2\varepsilon$ since $y_1$ receives 2 from $x_1$, receives $3-\varepsilon$ from it $p^+$-neighbors and transfers at most $\varepsilon$ to $z_1$. By $R_{22}$, $ch(y_1\rightarrow f_1)\ge \frac{5-2\varepsilon }{4}$ and $ch(y_1\rightarrow f_2)\ge \frac{5-2\varepsilon }{4}$. It follows that $ch(f_1\cup f_2\rightarrow v)\ge \frac{5-2\varepsilon }{4}\times 2$ as $n_b(f_1)=n_b(f_2)=1$. By $R_{23}$, $w^*(v)\ge -1-\varepsilon +\frac{5-2\varepsilon }{2}\ge 0$.

Otherwise, we assume that $d(x_1)\ge p$. It is easy to calculate that $w^\prime (u_2)\ge 3d(u_2)-10+3-\varepsilon +3-\varepsilon -2(d(u_2)-2)\ge d(u_2)-2\varepsilon$ since $u_2$ receives $3-\varepsilon$ from $x_1$ and u, respectively. By $R_{22}$, $ch(u_2\rightarrow f_4)\ge 1-\varepsilon$ and $ch(f_4\rightarrow v)\ge {1-\varepsilon }$ since $n_b(f_4)=1$. On the other hand, $w^\prime (x)\ge -4+2+3-\varepsilon \ge 1-\varepsilon$. By $R_{22}$, $ch(x\rightarrow v)\ge 1-\varepsilon$. Totally, $w^*(v)\ge -1-\varepsilon +(1-\varepsilon )+(1-\varepsilon )\ge 0$.

Subcase P833 $d(x_1)\le 9$ and $d(z_1)\le 9$.

Notice that min$\{d(x_1),d(y_1),d(z_1)\}\ge 4$ in this situation by Lemma 2.2. First we assume that $d(y_1)\le p-1$. It is not difficult to check that $w^\prime (z_1)\ge 3d(z_1)-10+3-\varepsilon -(1+\varepsilon )-\varepsilon -2(d(z_1)-3)\ge d(z_1)-2-3\varepsilon$ (noticing that $z_1$ receives $3-\varepsilon$ from its $p^+$-neighbors and transfers at most $1+\varepsilon$, $\varepsilon$ to $u_1$ and $y_1$, respectively). It follows that $ch(z_1\rightarrow \{f_2, f_3\})\ge \frac{2-3\varepsilon }{4}\times 2$ and $ch(\{f_2, f_3\}\rightarrow v)\ge \frac{2-3\varepsilon }{4}\times 2$ since $n_b(f_2)=n_b(f_3)=1$. By symmetry, $ch(x_1\rightarrow \{f_1, f_4\})\ge \frac{2-3\varepsilon }{4}\times 2$. We have $w^*(v)\ge -1-\varepsilon +\frac{2-3\varepsilon }{4}\times 4\ge 0$.

Otherwise, we assume that $d(y_1)\ge p$. Notice that $w^\prime (y)\ge -4+2+3-\varepsilon \ge 1-\varepsilon$ by $R_{11}$ and $R_{15}$. Hence, $ch(y\rightarrow v)\ge 1-\varepsilon$ by $R_{22}$.

Besides, we also calculate the charge transferred from $x_1$ to it incident faces.

If $d(x_1)\ge 5$, then $w^\prime (x_1)\ge 3d(x_1)-10+3-\varepsilon -(1+\varepsilon )-2(d(x_1)-2)\ge d(x_1)-4 -\varepsilon$ since $x_1$ receives $3-\varepsilon$ from $y_1$ and transfers at most $1+\varepsilon$ to $u_2$. It follows that $ch(x_1\rightarrow \{f_1, f_4\})\ge \frac{1-\varepsilon }{5}\times 2$, which induces that $w^*(v)\ge -1-\varepsilon +1-\varepsilon +\frac{1-\varepsilon }{5}\times 2\ge 0$ since $n_b(f_1)=n_b(f_4)=1$.

If $d(x_1)=4$, then by Lemma 2.7(2), $n_2(x_1)\le 2$. Hence, $w^\prime (x_1)\ge 2+3-\varepsilon -4-\frac{1}{3}\ge \frac{2}{3}-\varepsilon$. It follows that $ch(x_1\rightarrow \{f_1, f_4\})\ge \frac{2-3\varepsilon }{12}\times 2$, which induces that $w^*(v)\ge -1-\varepsilon +1-\varepsilon +\frac{2-3\varepsilon }{12}\times 2\ge 0$.

Finally, if $d(x_1)=3$, then by Lemma 2.7(1), $d(u_2)\ge 5$. We consider $u_2$. It is easy to check that $w^\prime (u_2)\ge 3d(u_2)-10+3-\varepsilon -\varepsilon -2(d(u_2)-2)\ge d(u_2)-3-2\varepsilon$ since $u_2$ receives $3-\varepsilon$ from u and transfers at most $\varepsilon$ to $x_1$. Hence $ch(u_2\rightarrow f_4)\ge \frac{2-2\varepsilon }{5}$ and $ch(f_4\rightarrow v)\ge \frac{2-2\varepsilon }{5}$, which induces that $w^*(v)\ge -1-\varepsilon +1-\varepsilon +\frac{2-2\varepsilon }{5}\ge 0$.