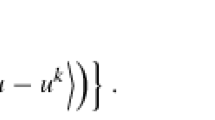An improved linear convergence of FISTA for the LASSO problem with application to CT image reconstruction

Abstract

The LASSO problem has been explored extensively for CT image reconstruction, the most useful algorithm to solve the LASSO problem is the FISTA. In this paper, we prove that FISTA has a better linear convergence rate than ISTA. Besides, we observe that the convergence rate of FISTA is closely related to the acceleration parameters used in the algorithm. Based on this finding, an acceleration parameter setting strategy is proposed. Moreover, we adopt the function restart scheme on FISTA to reconstruct CT images. A series of numerical experiments is carried out to show the superiority of FISTA over ISTA on signal processing and CT image reconstruction. The numerical experiments consistently demonstrate our theoretical results.

1 Introduction

LASSO (least absolute shrinkage and selection operator) is a regression analysis method that has been explored extensively for computed tomography (CT) image reconstruction, due to the potential of acquiring CT scans with lower X-ray dose while maintaining image quality. The LASSO problem, i.e. $L_1$ norm regularized least squares problem is:

$$\begin{aligned} \min _{\varvec{x}\in \mathbb {R}^{N}}\qquad \frac{1}{2}\Vert \varvec{b}-A\varvec{x}\Vert ^{2}+\lambda \Vert \varvec{x}\Vert _{1}, \end{aligned}$$

(1)

where $A\in \mathbb {R}^{M\times N}$ is a measurement matrix, $\varvec{b}\in \mathbb {R}^{M}$ is an observation, $\Vert \cdot \Vert$ denotes the Euclidean norm, $\Vert \varvec{x}\Vert _{1}=\sum _{i=1}^{n}|x_{i}|$ is the $L_{1}$ norm and $\lambda >0$ is a regularization parameter. It is well known that the LASSO problem is a convex optimization problem. Hence, there exist many exclusive and efficient algorithms, for instance, interior-point method Chen et al. (2001), least angle regression Efron et al. (2004), augmented lagrangian method (ALM) Yang et al. (2013) and iterative shrinkage thresholding algorithm (ISTA) Donoho (1995).

Due to the increasing demand for solving large-scale convex optimization problems, the accelerated gradient algorithm Nesterov (1983) has attracted much attention. By introducing the idea of accelerated gradient algorithm to ISTA, Beck and Teboulle have proposed a fast iterative shrinkage–thresholding algorithm Beck and Teboulle (2009) to solve the following problem:

$$\begin{aligned} \min _{\varvec{x}\in \mathbb {R}^{N}}\qquad F(\varvec{x})=f(\varvec{x})+g(\varvec{x}), \end{aligned}$$

(2)

where f is a smooth convex function and g is a continuous function but possibly nonsmooth. It is clear that (2) includes the LASSO problem as a special case.

It is well known that FISTA provides a global convergence rate of $\mathcal {O}(1/k^2)$ compared to the rate of $\mathcal {O}(1/k)$ by ISTA, where k is the iteration number Beck and Teboulle (2009). Recently, Tao et al. (2016) have established local linear convergence rates for both ISTA and FISTA on the LASSO problem under the assumption that the problem has a unique solution satisfying strict complementarity. Johnstone and Moulin (2015) have also shown that the sequence generated by FISTA is locally linearly convergent when applied to LASSO problem for a particular choice of acceleration parameters.

Although FISTA is superior to ISTA both on theoretical results and numerical performance, a common observation when running FISTA is the appearance of ripples or bumps in the trace of objective value near the optimal solution. Using a spectral analysis, Tao et al. (2016) have shown that FISTA slows down compared to ISTA when close enough to the optimal solution. To improve the convergence rate of FISTA, they switch to ISTA toward the end of the iteration process. On the other hand, O’Donoghue and Candès (2015) have proposed restart schemes for FISTA to avoid rippling behaviors. Moreover, Wen et al. (2017) have obtained a linear convergence rate of the sequence generated by FISTA with a fixed restart.

In contrast to the theoretical superiority on the global convergence rate, there is no result on the local convergence behavior demonstrating that FISTA is superior to ISTA. In this paper, utilizing the structure of measurement matrix A on the LASSO problem, we prove that FISTA has a better linear convergence rate than ISTA. We further observe that the convergence rate of FISTA is closely related to the acceleration parameters. Then the acceleration and regularization parameter setting strategies are proposed. A series of numerical experiments including signal processing and CT image reconstruction is carried out to compare ISTA with FISTA under different acceleration and regularization parameters. Moreover, we adopt the function restart scheme on FISTA to reconstruct CT images. The numerical experiments are consistent with our theoretical results.

The rest of this paper is organized as follows. In Sect. 2, some basic preliminaries are given. Then we prove a faster linear convergence rate of FISTA compared to ISTA in Sect. 3. Furthermore, in Sect. 4, we present some useful parameter setting strategies of FISTA. In Sect. 5, a series of numerical experiments are carried out, including signal recovery and CT image reconstruction, to show the effectiveness of FISTA. We conclude this paper in Sect. 6.

2 Preliminaries

In this section, we review the optimality conditions of the LASSO problem and the corresponding ISTA and FISTA, which then serve as the basis of further analysis in the following sections.

The first-order KKT optimality conditions for the LASSO problem are

$$\begin{aligned} A^{\top }(\varvec{b}-A\varvec{x})=\lambda \nu , \end{aligned}$$

where each component of $\nu$ satisfies:

$$\begin{aligned} {\left\{ \begin{array}{ll} \nu _{i}=\text {sign}(x_i), &{}\quad \text {if} \ x_i\ne 0,\\ -1\le \nu _{i}\le 1, &{}\quad \text {if} \ x_i= 0, \end{array}\right. }\quad \text {for} \ i=1, 2,\ldots ,n. \end{aligned}$$

Here the “sign” function is defined as:

$$\begin{aligned} \text {sign}(u):= {\left\{ \begin{array}{ll} 1,&{}\quad u>0,\\ 0,&{}\quad u=0,\\ -1,&{}\quad u<0. \end{array}\right. } \end{aligned}$$

In the following, we review the basic iterations of ISTA and FISTA for the LASSO problem. The basic step of ISTA can be reduced to

$$\begin{aligned} \begin{aligned} \varvec{x}^{n+1}&=\arg \min _{\varvec{x}}\left\{ \lambda \Vert \varvec{x}\Vert _{1}+\frac{L}{2}\left\| \varvec{x}-\left( \varvec{x}^{n}-\frac{1}{L}(A^{\top }A\varvec{x}^{n}-A^{\top }\varvec{b})\right) \right\| ^{2}\right\} \\&=\text {shr}_{\lambda /L}\left( \left( I-\frac{1}{L}A^{\top }A\right) \varvec{x}^{n}+\frac{1}{L}A^{\top }\varvec{b}\right) \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \text {shr}_{a}(u)&=\text {sign}(u)\max \{|u|-a, 0\}\\&={\left\{ \begin{array}{ll} \text {sign}(u)(|u|-a), &{}\quad \text {if} \ |u|>a,\\ 0, &{}\quad \text {otherwise},\end{array}\right. } \end{aligned} \end{aligned}$$

and L is the given constant which is greater than or equal to $\Vert A^{\top }A\Vert$.

As for FISTA, the difference from ISTA is that the shrinkage operator is not employed on the previous point $\varvec{x}^{n-1}$ but another point $\varvec{y}^{n}$, which uses a very specified linear combination of the previous two points $\{\varvec{x}^{n-1}, \varvec{x}^{n-2}\}$. The procedure of FISTA is presented as below.

For simplicity, $\Vert \cdot \Vert$ denotes the Euclidean norm. The support of $\varvec{x}\in \mathbb {R}^{n}$ is $\text {supp}(\varvec{x}):=\{i: |x_{i}|\ne 0, i=1, 2, \ldots ,n\}$. For any symmetric matrix $B\in \mathbb {R}^{n\times n}$, we denote its maximum and minimum eigenvalues respectively as $\sigma _{\text {max}}(B)$ and $\sigma _{\text {min}}(B)$. I is the identity matrix. For any matrix $A, B\in \mathbb {R}^{n\times n}$, $A\succeq B$ if and only if $A-B$ is a positive semidefinite matrix. For any index set S, we denote $B_{S}$ as the submatrix of B with the columns restricted to S and $\varvec{x}_{S}$ as the subvector consisting of only the components $x_{i}, i\in S$. $S^{c}$ represents the complementary set of S.

3 The improved linear convergence rate of FISTA

In this section, we establish the improved convergence rate of FISTA for LASSO problem.

For simplicity, $\mu$ denotes 1 / L, i.e. $0<\mu \le \Vert A\Vert ^{-2}$. Let

$$\begin{aligned} B_{\mu }(\varvec{x})=(I-\mu A^{\top }A)\varvec{x}+\mu A^{\top }\varvec{b}. \end{aligned}$$

We define the following partition of all indices $\{1, 2, \ldots , N\}$ into L and E.

Definition 1

Let $\varvec{x}^{*}$ be the optimal solution of the LASSO problem. Define

$$\begin{aligned} E:=\left\{ i:\left| [B_{\mu }(\varvec{x}^{*})]_{i}\right| \ge \lambda \mu \right\} , L:=\left\{ i:\left| [B_{\mu }(\varvec{x}^{*})]_{i}\right| <\lambda \mu \right\} . \end{aligned}$$

It is clear that $L\cup E=\{1, 2, \ldots , N\}$,

$$\begin{aligned} \text {supp}(\varvec{x}^{*})\subseteq E,~~\text {and}~~x^{*}_{i}=0,~\forall i\in L. \end{aligned}$$

The basic Step 3 of ISTA can be written as

$$\begin{aligned} \varvec{x}^{n+1}=\text {shr}_{\lambda \mu }\left( B_{\mu }(\varvec{x}^{n})\right) , \end{aligned}$$

while the fixed point of this operator is the optimal solution of the LASSO problem. As we all know, the sequence generated by ISTA for the LASSO problem has a local linear convergence rate Hale et al. (2008).

Lemma 1

Let $\{\varvec{x}^{n}\}$ be the sequence generated by ISTA for the LASSO problem and $\varvec{x}^{*}$ be the optimal solution. If $\sigma _{\text {min}}(A_{E}^{\top }A_{E})>0$, then

$$\begin{aligned} \Vert \varvec{x}^{n+1}-\varvec{x}^{*}\Vert \le \rho \Vert \varvec{x}^{n}-\varvec{x}^{*}\Vert . \end{aligned}$$

where $\rho =1-\mu \sigma _{\text {min}}(A_{E}^{\top }A_{E}), \rho \in (0,1)$.

The basic Step 4 of FISTA for the LASSO problem can be written as

$$\begin{aligned} \varvec{x}^{n+1}=\text {shr}_{\lambda \mu }\left( B_{\mu }(\varvec{y}^{n})\right) . \end{aligned}$$

Before establishing the improved linear convergence rate of FISTA, we present an important property first.

Lemma 2

Assume that the sequence $\{\varvec{x}^{n}\}$ generated by FISTA for the LASSO problem converges to $\varvec{x}^{*}$. Then, there exists an $n_{0}$ such that whenever $n\ge n_{0}$, for any $i\in L$

$$\begin{aligned} y^{n}_{i}=x^{n}_{i}=x^{*}_{i}=0, \end{aligned}$$

(5)

and for any $i\in E$

$$\begin{aligned} \text {sign}\left( \left[ B_{\mu }(\varvec{y}^{n})\right] _{i}\right) =\text {sign}\left( \left[ B_{\mu }(\varvec{x}^{n})\right] _{i}\right) =\text {sign}\left( \left[ B_{\mu }(\varvec{x}^{*})\right] _{i}\right) . \end{aligned}$$

(6)

Proof

By the continuity of $B_{\mu }(\varvec{x})$, $\forall \epsilon >0$, $\exists \delta >0$, s.t. $\left\| B_{\mu }(\varvec{x})-B_{\mu }(\varvec{x^{*}})\right\| < \epsilon$ if $\Vert x-x^{*}\Vert <\delta$. By the assumption that $\{\varvec{x}^{n}\}$ generated by FISTA converges to $\varvec{x}^{*}$, for $\delta$, there exists an $n_{0}$ such that whenever $n\ge n_{0}+2$,

$$\begin{aligned} \left\| \varvec{x}^{n-2}-\varvec{x}^{*}\right\| <\frac{\delta }{3}. \end{aligned}$$

As

$$\begin{aligned} \Vert \varvec{y}^{n}-\varvec{x}^{*}\Vert \le (1+\beta _{n})\Vert \varvec{x}^{n-1}-\varvec{x}^{*}\Vert +\beta _{n}\Vert \varvec{x}^{n-2}-\varvec{x}^{*}\Vert <\delta , \end{aligned}$$

$\{\varvec{y}^{n}\}$ converges to $\varvec{x}^{*}$ and

$$\begin{aligned} \left\| B_{\mu }(\varvec{x}^{n})-B_{\mu }(\varvec{x}^{*})\right\|<\epsilon ,~~~~\left\| B_{\mu }(\varvec{y}^{n})-B_{\mu }(\varvec{x}^{*})\right\| <\epsilon . \end{aligned}$$

First, we prove by contradiction that for $i\in L$, $x^{n}_{i}=x^{*}_{i}=0$ whenever $n\ge n_{0}+2$. Assuming it doesn’t hold, there exists an $i\in L$, a subsequence $\{n_k\}$ with $n_k>n_0$ such that $x^{n_k+1}_{i}\ne 0$. Hence

$$\begin{aligned} \begin{aligned} \left\| B_{\mu }(\varvec{x}^{n_k})-B_{\mu }(\varvec{x}^{*})\right\|&\ge \left| [B_{\mu }(\varvec{x}^{n_k})]_{i}-[B_{\mu }(\varvec{x}^{*})]_{i}\right| \\&\ge \lambda \mu -\left| [B_{\mu }(\varvec{x}^{*})]_{i}\right| \end{aligned} \end{aligned}$$

where $|[B_{\mu }(\varvec{x}^{*})]_{i}|<\lambda \mu$. It contradicts to the fact that $\left\{ B_{\mu }(\varvec{x}^{n})\right\}$ converges to $B_{\mu }(\varvec{x}^{*})$. Following the same procedure, we can prove for $i\in L$, $y^{n}_{i}=x^{*}_{i}=0$ whenever $n\ge n_{0}+2$. Therefore, $y^{n}_{i}=x^{n}_{i}=x^{*}_{i}=0,~\forall i\in L$.

Similarly, we can prove (6) by contradiction. Assuming it doesn’t hold, there exists an $i\in E$, a subsequence $\{n_k\}$ with $n_k>n_0+2$ such that $\text {sign}([B_{\mu }(\varvec{x}^{n_k})]_{i})\ne \text {sign}([B_{\mu }(\varvec{x}^{*})]_{i})$. Hence,

$$\begin{aligned} \begin{aligned} \left\| B_{\mu }(\varvec{x}^{n_k})-B_{\mu }(\varvec{x}^{*})\right\|&\ge \left| [B_{\mu }(\varvec{x}^{n_k})]_{i}-[B_{\mu }(\varvec{x}^{*})]_{i}\right| \\&\ge \left| [B_{\mu }(\varvec{x}^{n_k})]_{i}\right| +\left| [B_{\mu }(\varvec{x}^{*})]_{i}\right| >2\lambda \mu \end{aligned} \end{aligned}$$

contradicting again to the fact that $\left\{ B_{\mu }(\varvec{x}^{n})\right\}$ converges to $B_{\mu }(\varvec{x}^{*})$. We can also prove $\text {sign}([B_{\mu }(\varvec{y}^{n})]_{i})=\text {sign}([B_{\mu }(\varvec{x}^{*})]_{i}$ when $n\ge n_{0}+2$, in the same way. As a result, (6) holds.

This completes the proof. $\square$

We are now ready to prove the promised improved linear convergence rate of FISTA for the LASSO problem.

Theorem 1

Assume that the sequence $\{\varvec{x}^{n}\}$ generated by FISTA for the LASSO problem converges to $\varvec{x}^{*}$. If

$$\begin{aligned} 0<\mu \Vert A\Vert ^{2}<1-\frac{4\alpha }{(1+\alpha )^{2}},~~0<\alpha <1 \end{aligned}$$

and $\sigma _{\text {min}}(A_{E}^{\top }A_{E})>0$, then

$$\begin{aligned} \left\| \varvec{x}^{n}-\varvec{x}^{*}\right\| \le \prod _{k=1}^{n}\left[ \rho -\beta _{k}\left( 1-\rho \right) \right] \left\| \varvec{x}^{0}-\varvec{x}^{*}\right\| . \end{aligned}$$

where $\beta _{1}=0$ and $\beta _{k}\in [0, \alpha ], k\ge 2$.

Proof

By Lemma 2, we have $y^{n}_{i}=x^{n}_{i}=x^{*}_{i}=0,~ \forall i\in L$ and $\text {sign}\left( \left[ B_{\mu }(\varvec{y}^{n})\right] _{i}\right) =\text {sign}\left( \left[ B_{\mu }(\varvec{x}^{n})\right] _{i}\right) =\text {sign}\left( \left[ B_{\mu }(\varvec{x}^{*})\right] _{i}\right) ,~ \forall i\in E$ when $n\ge n_{0}+2$. Then $\left\| \varvec{h}_{L}^{n}\right\| =0$ and $\left\| \varvec{h}^{n}\right\| =\left\| \varvec{h}_{E}^{n}\right\|$ when $n\ge n_{0}+2$, where $\varvec{h}^n=\varvec{x}^{n}-\varvec{x}^{*}$. For simplicity, we assume that $n\ge n_{0}+2$ always holds.

For any $i\in E$, the following equation holds

$$\begin{aligned} \varvec{x}_{E}^{n}-\varvec{x}_{E}^{*}=P\left[ (1+\beta _{n})\left( \varvec{x}_{E}^{n-1}-\varvec{x}_{E}^{*}\right) -\beta _{n}\left( \varvec{x}_{E}^{n-2}-\varvec{x}_{E}^{*}\right) \right] , \end{aligned}$$

where

$$\begin{aligned} P=I-\mu A_{E}^{\top }A_{E},~~~\beta _{1}=0,~~~\beta _{k}\in [0, \alpha ],~~~k\ge 2. \end{aligned}$$

Denoting

$$\begin{aligned} F_{0}=I,~~F_{1}=P,~~F_{n}=P\left[ \left( 1+\beta _{n}\right) F_{n-1}-\beta _{n}F_{n-2}\right] , \end{aligned}$$

it follows that

$$\begin{aligned} \varvec{x}_{E}^{n}-\varvec{x}_{E}^{*}=F_{n}\left( \varvec{x}_{E}^{0}-\varvec{x}_{E}^{*}\right) . \end{aligned}$$

The mathematical induction is used to prove

$$\begin{aligned} 0\preceq \frac{(1+\alpha )}{2} PF_{n-1}\preceq F_{n}\preceq \left[ (1+\beta _{n})P-\beta _{n}I\right] F_{n-1}. \end{aligned}$$

(7)

First we have

$$\begin{aligned} F_{1}=P\preceq \left[ (1+\beta _{1})P-\beta _{1}I\right] F_{0}=P \end{aligned}$$

as $\beta _{1}=0$.

Next, we prove $P\succeq 0$. Since $0<\mu \Vert A\Vert ^2<1-4\alpha /(1+\alpha )^{2}$, we have $0<\mu \Vert A_{E}\Vert ^2<1-4\alpha /(1+\alpha )^{2}$. Therefore,

$$\begin{aligned} P=I-\mu A_{E}^{\top }A_{E}\succeq \frac{4\alpha }{(1+\alpha )^{2}}I \succeq 0. \end{aligned}$$

As $0<\alpha <1$, it follows

$$\begin{aligned} 0\preceq \frac{(1+\alpha )}{2} PF_{0}\preceq F_{1}\preceq \left[ (1+\beta _{1})P-\beta _{1}I\right] F_{0}. \end{aligned}$$

Second, assuming

$$\begin{aligned} 0\preceq \frac{(1+\alpha )}{2} PF_{n-1}\preceq F_{n}\preceq \left[ (1+\beta _{n})P-\beta _{n}I\right] F_{n-1}, \end{aligned}$$

we shall prove that

$$\begin{aligned} 0\preceq \frac{(1+\alpha )}{2} PF_{n}\preceq F_{n+1}\preceq \left[ (1+\beta _{n+1})P-\beta _{n+1}I\right] F_{n}. \end{aligned}$$

Since

$$\begin{aligned} F_{n}\preceq [(1+\beta _{n})P-\beta _{n}I]F_{n-1}\preceq PF_{n-1}, \end{aligned}$$

we have

$$\begin{aligned} F_{n+1}=P[(1+\beta _{n+1})F_{n}-\beta _{n+1}F_{n-1}]\preceq [(1+\beta _{n+1})P-\beta _{n+1}I]F_{n}. \end{aligned}$$

On the other hand,

$$\begin{aligned} \begin{aligned} F_{n+1}&=P[(1+\beta _{n+1})F_{n}-\beta _{n+1}F_{n-1}]\\&\succeq \left[ (1+\beta _{n+1})P-\beta _{n+1}P\left( \frac{(1+\alpha )}{2}P\right) ^{-1}\right] F_{n}, \end{aligned} \end{aligned}$$

where the inequality is due to the fact that

$$\begin{aligned} \frac{(1+\alpha )}{2} PF_{n-1}\preceq F_{n},~\frac{(1+\alpha )}{2} P\succeq 0. \end{aligned}$$

To show

$$\begin{aligned} 0\preceq \frac{(1+\alpha )}{2}PF_{n}\preceq F_{n+1}, \end{aligned}$$

we only need to prove

$$\begin{aligned} \left[ \left( 1+\beta _{n+1}\right) P-\beta _{n+1}P\left( \frac{(1+\alpha )}{2}P\right) ^{-1}\right] \succeq \frac{(1+\alpha )}{2}P \end{aligned}$$

i.e.

$$\begin{aligned} \left[ \frac{1}{2}(1+\alpha )(1+\beta _{n+1})-\frac{1}{4}(1+\alpha )^{2}\right] P^{2}\succeq \beta _{n+1}P. \end{aligned}$$

(8)

Since

$$\begin{aligned} P\succeq \frac{4\alpha }{(1+\alpha )^{2}}I,~\frac{1}{2}(1+\alpha )(1+\beta _{n+1})-\frac{1}{4}(1+\alpha )^{2}>0 \end{aligned}$$

and

$$\begin{aligned} \frac{4\alpha }{(1+\alpha )^{2}}\left[ \frac{1}{2}(1+\alpha )(1+\beta _{n+1})-\frac{1}{4}(1+\alpha )^{2}\right] \ge \beta _{n+1}, \end{aligned}$$

Eq. (8) holds.

In conclusion, (7) holds. By (7), we obtain

$$\begin{aligned} \Vert F_{n}\Vert \le \prod _{k=1}^{n}\left[ \rho -\beta _{k}\left( 1-\rho \right) \right] \end{aligned}$$

where

$$\begin{aligned} 0\le \frac{4\alpha }{(1+\alpha )^{2}}\le \rho =\Vert P\Vert <1. \end{aligned}$$

This completes the proof. $\square$

Remark 1

From the proof of Theorem 1, for any $k\ge 1$, we have $0\le \beta _{k}\le \alpha$, $\rho <1$. Thus, $\rho -\beta _{k}\left( 1-\rho \right) <\rho$. On the other hand, for any $k\ge 1$

$$\begin{aligned} \frac{\beta _{k}}{1+\beta _{k}}<\frac{4\alpha }{(1+\alpha )^{2}}\le \rho . \end{aligned}$$

So we have $\left[ \rho -\beta _{k}\left( 1-\rho \right) \right] >0$, indicating that the convergence rate of FISTA for the LASSO probelm is better than that of ISTA.

4 Parameter setting strategies

In this section, we will discuss some setting strategies for the acceleration and regularization parameters.

4.1 Acceleration parameter

From Theorem 1, we can observe that the linear convergence rate of FISTA is closely related to the acceleration parameters $\beta _{n}$. If $\{\beta _{n}^{1}\}$ and $\{\beta _{n}^2\}$ are two increasing sequences with values in the range of $(0,\alpha )$ and $\beta _{n}^{1}<\beta _{n}^2$, FISTA with acceleration parameter $\{\beta _{n}^2\}$ is converging faster to the optimal solution compared to that with $\{\beta _{n}^1\}$.

Beck and Teboulle (2009) have proposed the following choice of acceleration parameters for FISTA, with

$$\begin{aligned} \beta _{n}=\frac{t^{n}-1}{t^{n+1}},\quad \text {where}\ t^{n+1}=\frac{1+\sqrt{1+4(t^{n})^2}}{2},\quad t^0=t^1=1, \end{aligned}$$

while Tseng (2008) has proposed a FISTA with acceleration parameters

$$\begin{aligned} \beta _{n}=\frac{n-2}{n+1}. \end{aligned}$$

In the section of numerical experiments, we will compare the convergence rates of FISTA with different $\{\beta _{n}\}$ to demonstrate the theoretical results.

4.2 Regularization parameter

It is well known that the solution quality of LASSO problem is closely related to the regularization parameter $\lambda$. However, to set a proper value of regularization parameter is a very hard problem. Nevertheless, when some prior information (e.g., sparsity) is known, it is realistic to set the regularization parameter more reasonably and intelligently Xu et al. (2012).

Similar to the setting strategies in Xu et al. (2012), we set $\lambda$ as follows. Assume $\varvec{x}^{*}$ is the optimal solution of the LASSO problem with k-sparsity. Without loss of generality, assume $\left[ B_{\mu }(\varvec{x}^{*})\right] _{1}\ge \left[ B_{\mu }(\varvec{x}^{*})\right] _{2}\ge \cdots \ge \left[ B_{\mu }(\varvec{x}^{*})\right] _{N}$. Then,

$$\begin{aligned}&\left| \left[ B_{\mu }(\varvec{x}^{*})\right] _{i}\right| \ge \lambda \mu \Leftrightarrow i\in \{1,2,\ldots ,k\}\\&\left| \left[ B_{\mu }(\varvec{x}^{*})\right] _{i}\right| <\lambda \mu \Leftrightarrow i\in \{k+1,k+2,\ldots ,N\} \end{aligned}$$

which implies

$$\begin{aligned} \lambda \in \left[ \left| \left[ B_{\mu }(\varvec{x}^{*})\right] _{k+1}\right| /\mu , \left| \left[ B_{\mu }(\varvec{x}^{*})\right] _{k}\right| /\mu \right] \end{aligned}$$

Instead of the optimal solution, we may use any known approximations of $\varvec{x}^{*}$, say, we can take

$$\begin{aligned} \lambda ^{*}=\left| \left[ B_{\mu }(\varvec{x}^{n})\right] _{k+1}\right| /\mu \end{aligned}$$

(9)

in applications.

4.3 FISTA with restart scheme

A common observation when running FISTA is the appearance of ripples or bumps in the trace of the objective value near the optimal solution. To improve the convergence rate of the FISTA, O’Donoghue and Candès (2015) proposed two restart schemes:

• Function scheme: restart whenever

  $$\begin{aligned} F(\varvec{x}^{k})>F(\varvec{x}^{k-1}). \end{aligned}$$

• Gradient scheme: restart whenever

  $$\begin{aligned} \nabla F(\varvec{y}^{n})(\varvec{x}^{n}-\varvec{x}^{n-1})>0. \end{aligned}$$

Here, we will use function restart scheme to improve the FISTA, named as IMFISTA. If $F(\varvec{x}^{n})>F(\varvec{x}^{n-1})$, we reset the acceleration parameter $\beta _{n}=0$.

5 Numerical experiments

In this section, we conduct a series of numerical experiments to demonstrate the validity of the theoretical analysis on the convergence of ISTA and FISTA. Furthermore, to demonstrate the parameter setting strategies, FISTA with different acceleration parameters are also tested. The sparse signal and CT image reconstruction problems are considered in this section.

The numerical experiments are carried out using MATLAB 2012(b) and running on a PC with 2.50 GHZ CPU processor and 8 GB of RAM. The error precision $\epsilon$ is set to $10^{-6}$. The iteration bounds for algorithms in signal and image recovery are set to be 3000 and 1000, respectively.

5.1 Signal recovery

The sparse signal recovery problem has attracted a considerable amount of attention in the past decade Donoho (2006). This can be modeled as the LASSO problem. Here we consider a real-valued N-length ($N=2000$) signal $\varvec{x}$ without noise, where $\varvec{x}$ is K-sparse with $K=20$.

Table 1 Recovery results of a signal with different algorithms

The experiment then aims to recover a signal $\varvec{x}\in \mathbb {R}^{2000}$ from $M=200$ measurements by $\varvec{y}=A\varvec{x}$. The measurement matrix A is taken as the Gaussian random matrix, as suggested in Donoho (2006). The recovery precision is evaluated by the relative error (RE), defined as $\text {RE}=\Vert \varvec{x}-\varvec{x}^{*}\Vert /\Vert \varvec{x}^{*}\Vert$, where $\varvec{x}$ and $\varvec{x}^{*}$ represent the recovered and original signal respectively.

We test ISTA, FISTA and IMFISTA with $\beta _{n}=(t^{n-1}-1)/t^n$ and $\beta _{n}=(n-2)/(n+1)$, when $\lambda =0.0001$ and $\lambda =\lambda ^{*}$. For each case, the REs, the CPU times and the iteration numbers for all the algorithms are recorded. Some of the numerical results are listed in Table 1.

Fig. 1

FISTA and IMFISTA with $\lambda =0.0001$

FISTA and IMFISTA with $\beta _{n}=(t^{n-1}-1)/t^n$ are denoted by $\text {FISTA}_{1}$ and $\text {IMFISTA}_{1}$, respectively. FISTA and IMFISTA with $\beta _{n}=(n-2)/(n+1)$ are denoted by $\text {FISTA}_{2}$ and $\text {IMFISTA}_{2}$, respectively. It can be seen from Table 1 that $\text {IMFISTA}_{1}$ and $\text {IMFISTA}_{2}$ perform best in all the five algorithms, no matter $\lambda =0.0001$ or $\lambda =\lambda ^{*}$.

Fig. 2

FISTA and IMFISTA with $\lambda =\lambda ^{*}$

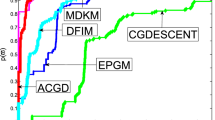
For a clearer illustration, Figs. 1 and 2 show how the REs vary with the iterations, highlighting that the IMFISTA has a faster convergence rate than the FISTA.

Fig. 3

FISTA with different $\beta _{n}$

Moreover, to demonstrate the theoretical results of the linear convergence rate of FISTA, we test FISTA with different multiples of $\beta _{n}=(n-2)/(n+1)$. Letting $\beta _{n}^{1}=0.2\beta _{n}$, $\beta _{n}^{2}=0.4\beta _{n}$, $\beta _{n}^{3}=0.6\beta _{n}$, $\beta _{n}^{4}=0.8\beta _{n}$, and $\beta _{n}^{5}=\beta _{n}$, we also illustrate numerical results in Fig. 3. As shown, FISTA with $\beta _{n}^{4}$ is converging fastest.

5.2 CT image recovery

We consider the problem of recovering the head phantom image ($256 \times 256$) (Fig. 4). The image can be expressed as a 65,536-dimensional vector $\varvec{x}$. It has a wavelet coefficient sequence $\varvec{\alpha }$ that is compressible Devore and Jawerth (1992), where $\varvec{x}=W^{\top }\varvec{\alpha }$, W is the discrete orthogonal wavelet transform matrix. We select Fourier matrix as the measurement matrix A.

Fig. 4

Original and compressed CT image

The experiment aims to recover the wavelet coefficient sequence $\varvec{\alpha }$ through the following model:

$$\begin{aligned} \min \qquad \Vert \varvec{y}-AW^{\top }\varvec{\alpha }\Vert ^{2}+\lambda \Vert \varvec{\alpha }\Vert _{0} \end{aligned}$$

where $\varvec{\alpha }$ is the wavelet coefficient sequence of the image $\varvec{x}$, $\lambda >0$ is a regularization parameter, $A\in \mathbb {R}^{M\times N}$ is a Fourier matrix, $W\in \mathbb {R}^{N\times N}$ is a discrete orthogonal wavelet transform matrix and $\varvec{y}$ is an observation.

Table 2 Recovery results of a CT image with different algorithms

Fig. 5

FISTA and IMFISTA with $\lambda =0.001$

Fig. 6

FISTA and IMFISTA with $\lambda =\lambda ^{*}$

We compare the performances of the ISTA, FISTA and IMFISTA on recovering these two images. The performance of each algorithm is measured in terms of signal-to-noise ratio (SNR), which is defined as

$$\begin{aligned} 10\lg \frac{\Vert \overline{\varvec{x}}-\text {mean}(\overline{\varvec{x}})\Vert _{2}^{2}}{\Vert \overline{\varvec{x}}-\varvec{x}\Vert _{2}^{2}}, \end{aligned}$$

where $\varvec{x}$ is the original image and $\overline{\varvec{x}}$ is the image recovered from the measurements by an algorithm.

First, we recovery the head phantom image generated by MATLAB. The sampling rate is measured as $M/N=0.39$. The detailed results of image recovery under different algorithms are listed in Table 2. Obviously, FISTA and IMFISTA with $\beta _{n}=(n-2)/(n+1)$ are faster than that with $\beta _{n}=(t^{n-1}-1)/t^n$, while IMFISTA is faster than FISTA.

Fig. 7

ISTA, FISTA and IMFISTA for CT image reconstruction

Fig. 8

FISTA with different $\beta _{n}$ for CT image reconstruction

Similarly, Figs. 5 and 6 show how the REs vary with the iterations, highlighting that the IMFISTA has a faster convergence rate than the FISTA.

Then, we recover the head phantom CT image Fig. 4. The sampling rate is measured as $M/N=0.31$. We set $\lambda =\lambda ^{*}$. Figure 7 shows how the REs vary with the iterations. We observe that FISTA is nearly the same as IMFISTA when RE is monotonically decreasing.

Moreover, we also demonstrate the theoretical results of the linear convergence rate of FISTA. Different acceleration parameters are tested, including $\beta _{n}^{1}=0.2\beta _{n}$, $\beta _{n}^{2}=0.4\beta _{n}$, $\beta _{n}^{3}=0.6\beta _{n}$, $\beta _{n}^{4}=0.8\beta _{n}$, and $\beta _{n}^{5}=\beta _{n}$. As shown in Fig. 8, FISTA with $\beta _{n}^{5}$ is converging fastest.

6 Conclusion

In this paper, we have proven that the FISTA has a better linear convergence rate than the ISTA. Besides, some useful insights for the acceleration and regularization parameter setting strategies have been derived from the theoretical result. Moreover, we have successfully implemented function restart scheme on the FISTA to reconstruct CT images. Both signal processing and CT image reconstruction are consistently demonstrating our theoretical results.

However, we have to point out that the local convergence rates of FISTA for general convex optimization is still unknown. The convergence rate of FISTA with restart schemes is also unknown, although it has been implemented on many applications, such as inpatient bed allocation Chang and Zhang (2019), healthcare facility layout Gai and Ji (2019) and the operation nurse problem Zhong and Bai (2019). These are interesting points for future research.