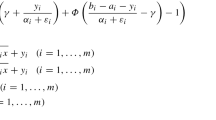Global probability maximization for a Gaussian bilateral inequality in polynomial time

Abstract

The present paper investigates Gaussian bilateral inequalities in view of solving related probability maximization problems. Since the function f representing the probability of satisfaction of a given Gaussian bilateral inequality is not concave everywhere, we first state and prove a necessary and sufficient condition for negative semi-definiteness of the Hessian. Then, the (nonconvex) problem of globally maximizing f over a given polyhedron in $\mathbb {R}^{n}$ is adressed, and shown to be polynomial-time solvable, thus yielding a new-comer to the (short) list of nonconvex global optimization problems which can be solved exactly in polynomial time. Application to computing upper bounds to the maximum joint probability of satisfaction of a set of m independent Gaussian bilateral inequalities is discussed and computational results are reported.

Appendices

Appendix 1 : Results used in proof of Theorem 1

We provide in this Appendix two results which are used in the proof of Theorem 1.

Proposition 5

H denoting the Hessian of the function $\varPhi (\frac{b-\mu ^{T}x}{\sqrt{x^{T}\varSigma x}})+\varPhi (\frac{\mu ^{T}x-a}{\sqrt{x^{T}\varSigma x}})-1$, checking negative semi-definiteness of H is equivalent to checking negative semi-definiteness of

$$\begin{aligned} \bar{H}=-\alpha \frac{VV^{T}}{\left\| V\right\| ^{2}} -\beta \frac{[VW^{T}+WV^{T}]}{\left\| V\right\| }-WW^{T}-I \end{aligned}$$

(7)

where $\alpha$ and $\beta$ are defined by (1) and (2) in the statement of Theorem 1, and $V=\varSigma ^{1/2}x$ and $W=\varSigma ^{-1/2}\mu$.

Proof

Using the expressions given in the proof of Theorem 1 in [12] , the Hessian of $\varPhi (\frac{b-\mu ^{T}x}{\sqrt{x^{T}\varSigma x}})$ is equal to :

$$\begin{aligned} H_{b}=\frac{e^{\frac{-\theta _{b}}{2}}(b-\mu ^{T}x)}{\sqrt{2\pi } (x^{T}\varSigma x)^{3/2}}\widehat{H}_{b} \end{aligned}$$

with:

$$\begin{aligned} \widehat{H}_{b}=(3-\theta _{b})\frac{\varSigma x(\varSigma x)^{T}}{x^{T}\varSigma x}+ \frac{(1-\theta _{b})}{(b-\mu ^{T}x)}(\varSigma x\mu ^{T}+\mu (\varSigma x)^{T})-\mu \mu ^{T}-\varSigma \end{aligned}$$

where $\theta _{b}=\frac{(b-\mu ^{T}x)^{2}}{x^{T}\varSigma x}$. Since $\frac{(1-\theta _{b})}{(b-\mu ^{T}x)}$can be rewritten as $\frac{ (1-\theta _{b})}{\sqrt{\theta _{b}}}\frac{1}{\sqrt{x^{T}\varSigma x}}$, an equivalent expression for $\widehat{H}_{b}$ is:

$$\begin{aligned} \widehat{H}_{b}=(3-\theta _{b})\frac{\varSigma x(\varSigma x)^{T}}{x^{T}\varSigma x}+ \frac{(1-\theta _{b})}{\sqrt{\theta _{b}}}\frac{(\varSigma x\mu ^{T}+\mu (\varSigma x)^{T})}{\sqrt{x^{T}\varSigma x}}-\mu \mu ^{T}-\varSigma \end{aligned}$$

(8)

In a similar way, we get the expression of the Hessian of $\varPhi (\frac{\mu ^{T}x-a}{\sqrt{x^{T}\varSigma x}})$ as :

$$\begin{aligned} H_{a}=\frac{e^{\frac{-\theta _{a}}{2}}(\mu ^{T}x-a)}{\sqrt{2\pi } (x^{T}\varSigma x)^{3/2}}\widehat{H}_{a} \end{aligned}$$

with:

$$\begin{aligned} \widehat{H}_{a}=(3-\theta _{a})\frac{\varSigma x(\varSigma x)^{T}}{x^{T}\varSigma x}+ \frac{(1-\theta _{a})}{\sqrt{\theta _{a}}}\frac{(\varSigma x\mu ^{T}+\mu (\varSigma x)^{T})}{\sqrt{x^{T}\varSigma x}}-\mu \mu ^{T}-\varSigma \end{aligned}$$

(9)

and $\theta _{a}=\frac{(\mu ^{T}x-a)^{2}}{x^{T}\varSigma x}$.

Let $\pi _{a}=e^{\frac{-\theta _{a}}{2}}(\mu ^{T}x-a)$ and $\pi _{b}=e^{ \frac{-\theta _{b}}{2}}(b-\mu ^{T}x)$. Note that $\pi _{a}\ge 0$, $\pi _{b}\ge 0$ and $\pi _{a}+\pi _{b}>0$ since it has been assumed that $a\le \mu ^{T}x\le b$ and $a<b$.

Then $H=\triangledown _{x}^{2}$ $\varPhi (\frac{b-\mu ^{T}x}{\sqrt{x^{T}\varSigma x }})+\triangledown _{x}^{2}\varPhi (\frac{\mu ^{T}x-a}{\sqrt{x^{T}\varSigma x}})$ can be written as:

$$\begin{aligned} H=\frac{1}{\sqrt{2\pi }(x^{T}\varSigma x)^{3/2}}(\pi _{a}\widehat{H}_{a}+\pi _{b}\widehat{H}_{b}). \end{aligned}$$

Checking negative semi-definiteness of H is equivalent to checking negative semi-definiteness of $\pi _{a}\widehat{H}_{a}+\pi _{b}\widehat{H} _{b}$ and this, in turn, is equivalent to checking negative semi-definiteness of :

$$\begin{aligned} \overline{H}=\varSigma ^{-1/2}(\frac{\pi _{a}\widehat{H}_{a}+\pi _{b}\widehat{H }_{b}}{\pi _{a}+\pi _{b}})\varSigma ^{-1/2}=\frac{\pi _{a}\overline{H_{a}}+\pi _{b}\overline{H_{b}}}{\pi _{a}+\pi _{b}} \end{aligned}$$

where $\overline{H_{a}}=\varSigma ^{-1/2}\widehat{H}_{a}\varSigma ^{-1/2}$ and $\overline{H_{b}}=\varSigma ^{-1/2}\widehat{H}_{b}\varSigma ^{-1/2}$.

Now, setting $V=\varSigma ^{1/2}x$ and $W=\varSigma ^{-1/2}\mu$, and denoting I the $n \times n$ unit matrix, it is easily seen that:

$$\begin{aligned} \overline{H_{a}}=(3-\theta _{a})\frac{VV^{T}}{\left\| V\right\| ^{2}}+ \frac{(1-\theta _{a})}{\sqrt{\theta _{a}}}\frac{[VW^{T}+WV^{T}]}{\left\| V\right\| }-WW^{T}-I \end{aligned}$$

(10)

and :

$$\begin{aligned} \overline{H_{b}}=(3-\theta _{b})\frac{VV^{T}}{\left\| V\right\| ^{2}}+ \frac{(1-\theta _{b})}{\sqrt{\theta _{b}}}\frac{[VW^{T}+WV^{T}]}{\left\| V\right\| }-WW^{T}-I \end{aligned}$$

(11)

Introducing the coefficients :

$$\begin{aligned} \alpha= & {} \frac{\pi _{a}(\theta _{a}-3)+\pi _{b}(\theta _{b}-3)}{\pi _{a}+\pi _{b}}=-3+\frac{e^{\frac{-\theta _{a}}{2}}(\theta _{a})^{\frac{3}{2}}+e^{\frac{-\theta _{b}}{2}}(\theta _{b})^{\frac{3}{2}}}{ e^{\frac{-\theta _{a}}{2}}\sqrt{\theta _{a}}+e^{\frac{-\theta _{b}}{2}}\sqrt{\theta _{b}}} \end{aligned}$$

(12)

$$\begin{aligned} \beta= & {} \frac{\pi _{a}\frac{\left( \theta _{a}-1\right) }{\sqrt{\theta _{a}}}+\pi _{b}\frac{ \left( \theta _{b}-1\right) }{\sqrt{\theta _{b}}}}{\pi _{a}+\pi _{b}} =\frac{e^{\frac{-\theta _{a}}{2}}(\theta _{a}-1)+e^{\frac{-\theta _{b} }{2}}(\theta _{b}-1)}{e^{\frac{-\theta _{a}}{2}}\sqrt{\theta _{a}}+e^{\frac{ -\theta _{b}}{2}}\sqrt{\theta _{b}}} \end{aligned}$$

(13)

we get expression (7) for $\bar{H}$. $\square$

Next, given two vectors $Y \in \mathbb {R}^n, Z \in \mathbb {R}^n (Y\ne 0, Z\ne 0)$, we prove the following result concerning the largest eigenvalue $\bar{\lambda }$ of the $n \times n$ matrix $YY^{T}-ZZ^{T}$, with rank at most 2:

Proposition 6

• (i) The largest eigenvalue for $YY^{T}-ZZ^{T}$ reads:

  $$\begin{aligned} \bar{\lambda }=\dfrac{\parallel Y \parallel ^{2}-\parallel Z \parallel ^{2}+\sqrt{\left( \parallel Y \parallel ^{2}+\parallel Z \parallel ^{2} \right) ^{2}-4\left( Z^{T}Y\right) ^{2}}}{2} \end{aligned}$$

  (14)

• (ii) A necessary and sufficient condition for ensuring $\bar{\lambda } \le 1$ is

  $$\begin{aligned} \parallel Y \parallel ^{2}-\parallel Z \parallel ^{2}+\parallel Y \parallel ^{2}\parallel Z \parallel ^{2}-\left( Z^{T}Y\right) ^{2} \le 1 \end{aligned}$$

  (15)

Proof

• (i) Since the special case when Y and Z are colinear is easily checked to be encompassed by (14), it is not restrictive to assume that Y and Z are linearly independent. First, it is observed that the two eigenvectors corresponding to the two possibly nonzero eigenvalues necessarily lies in the subspace generated by Y and Z, and this is an easy exercice to show that the two eigenvalues looked for coincide with the eigenvalues of the $2 \times 2$ matrix

  $$\begin{aligned} \left[ \begin{array}{cc} \parallel Y \parallel ^{2} &{} \left( Z^{T}Y\right) \\ -\left( Z^{T}Y\right) &{} -\parallel Z \parallel ^{2} \end{array} \right] \end{aligned}$$

  The corresponding characteristic equation reads:

  $$\begin{aligned} \lambda ^{2}+\left( \parallel Z \parallel ^{2}-\parallel Y \parallel ^{2}\right) \lambda - \parallel Y \parallel ^{2} \parallel Z \parallel ^{2}+\left( Z^{T}Y\right) ^{2} = 0 \end{aligned}$$

  the discriminant of which is:

  $$\begin{aligned} {\varDelta }= & {} \left( \parallel Z \parallel ^{2}-\parallel Y \parallel ^{2}\right) ^{2}+4 \parallel Y \parallel ^{2} \parallel Z \parallel ^{2}-4\left( Z^{T}Y\right) ^{2} \\= & {} \left( \parallel Z \parallel ^{2}+\parallel Y \parallel ^{2}\right) ^{2}-4\left( Z^{T}Y\right) ^{2} \end{aligned}$$

  From this, (14) immediatly follows.

• (ii) In view of (14), $\bar{\lambda } \le 1$ can be rewritten as:

  $$\begin{aligned} \sqrt{\left( \parallel Z \parallel ^{2}+\parallel Y \parallel ^{2}\right) ^{2}-4\left( Z^{T}Y\right) ^{2}} \le 2-\parallel Y \parallel ^{2}+\parallel Z \parallel ^{2} \end{aligned}$$

  which, after squaring, yields:

  $$\begin{aligned} 4\parallel Y \parallel ^{2}\parallel Z \parallel ^{2}-4\left( Z^{T}Y\right) ^{2}+4\parallel Y \parallel ^{2}-4\parallel Z \parallel ^{2} \le 4 \end{aligned}$$

  thus completing the proof.

$\square$

Appendix 2 : Polynomial algorithm BPM

Based on Theorem 2, we provide here the formal statement of a polynomial-time algorithm to determine the maximum of $\hat{\varPsi }\left( t\right)$ on $\left[ t_{\min },t_{\max } \right]$ within a confidence interval of width less than $\epsilon$. The interval reduction technique used here is the well-known golden section search method, which asymptotically requires a minimum number of function evaluations.

In each step of the procedure, the width of the confidence interval is reduced by the factor $r\simeq 0.618$, therefore an upper bound on the number q of iterations required to meet the requested accuracy $\epsilon$ is such that:

$$\begin{aligned} \frac{\left( b-a\right) }{2} r^{q} < \epsilon \le \frac{\left( b-a \right) }{2} r^{q-1} \end{aligned}$$

or equivalently: $q=\lceil \frac{1}{\ln (\frac{1}{r})} \left( \ln \left( \frac{1}{\epsilon } \right) + \ln \left( \frac{b-a}{2} \right) \right) \rceil$. As stated in the proof of Theorem 2, this bound is proportional to $\ln \left( \frac{1}{\epsilon } \right)$, and, since each evaluation of $\widehat{\varPsi }(t)$ is computable in polynomial time, this shows that (BPM) runs in polynomial time.