Abstract
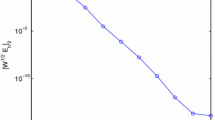
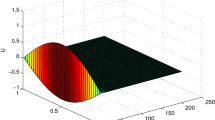
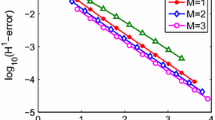
The solution of differential equations with singular source terms contains the local jump discontinuity in general and its spectral approximation is oscillatory due to the Gibbs phenomenon. To minimize the Gibbs oscillations near the local jump discontinuity and improve convergence, the regularization of the approximation is needed. In this note, a simple derivative of the discrete Heaviside function H c (x) on the collocation points is used for the approximation of singular source terms δ(x−c) or δ (n)(x−c) without any regularization. The direct projection of H c (x) yields highly oscillatory approximations of δ(x−c) and δ (n)(x−c). In this note, however, it is shown that the direct projection approach can yield a non-oscillatory approximation of the solution and the error can also decay uniformly for certain types of differential equations. For some differential equations, spectral accuracy is also recovered. This method is limited to certain types of equations but can be applied when the given equation has some nice properties. Numerical examples for elliptic and hyperbolic equations are provided.
Similar content being viewed by others
References
Carlson, H.A., Berkooz, G., Lumley, J.L.: Direct numerical simulation of flow in a channel with complex, time-dependent wall geometries: A pseudospectral method. J. Comput. Phys. 121, 155–175 (1995)
Engquist, B., Tornberg, A.-K., Tsai, R.: Discretization of Dirac delta function in level set methods. J. Comput. Phys. 207, 28–51 (2005)
Goldstein, D., Handler, R., Sirovich, L.: Modeling a non-slip flow boundary with an external force field. J. Comput. Phys. 105, 354–366 (1993)
Gottlieb, D., Orszag, S.: Numerical Analysis of Spectral Methods: Theory and Applications. SIAM, Philadelphia (1977)
Hesthaven, J.S., Gottlieb, S., Gottlieb, D.: Spectral methods for time-dependent problems. Cambridge Univ. Press, Cambridge (2007)
Huang, Y., Kouri, D., Hoffman, D.K.: General, energy-separable Faber polynomial representation of operator functions: Theory and application in quantum scattering. J. Chem. Phys. 101(12), 10493–10506 (1994)
Jung, J.-H., Khanna, G., Nagle, I.: A spectral collocation approximation of one-dimensional head-on collisions of black holes. Class. Quantum Gravity (2007, submitted). Also the book of abstracts of ICOSAHOM 2007 (2007)
Lousto, C.O., Price, R.H.: Head-on collisions of black holes: the particle limit. Phys. Rev. D 55, 2124–2138 (1997)
McQueen, D.M., Peskin, C.S.: A three-dimensional computational method for blood flow in the heart. II. Contractile fibers. J. Comput. Phys. 82, 289–297 (1989)
Mohd-Yusof, J.: Interaction of massive particles with turbulence. Ph.D. Thesis. Cornell University (1996)
Moncrief, V.: Gravitational perturbations of spherically symmetric systems. I. The exterior problem. Ann. Phys. 88, 323–342 (1974)
Peskin, C.S.: Numerical analysis of blood flow in the heart. J. Comput. Phys. 25, 220–252 (1977)
Peskin, C.S.: The immersed boundary method. Acta Numer. 11, 479–517 (2002)
Peskin, C.S., McQueen, D.M.: Fluid dynamics of the heart and its valves. Case Studies in Mathematical Modeling: Ecology, Physiology, and Cell Biology, pp. 3009–3337 (1996)
Shu, C.-W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes II. J. Comput. Phys. 83, 32–78 (1989)
Tornberg, A.-K., Engquist, B.: Numerical approximations of singular source terms in differential equations. J. Comput. Phys. 200, 462–488 (2004)
Trefethen, N.: Spectral Methods in MATLAB. SIAM, Philadelphia (2000)
Waldén, J.: On the approximation of singular source terms in differential equations. Numer. Methods Partial Differ. Equ. 15, 503–520 (1999)
Wei, G.W., Zhao, Y.B., Xiang, Y.: Discrete singular convolution and its application to the analysis of plates with internal supports. Part 1: Theory and algorithm. Int. J. Numer. Methods Eng. 55, 913–946 (2002)
Zerilli, F.J.: Effective potential for even-parity Regge-Wheeler gravitational perturbation equations. Phys. Rev. Lett. 24, 737–738 (1970)
Author information
Authors and Affiliations
Corresponding author
Additional information
The current address: Department of Mathematics, State University of New York at Buffalo, Buffalo, NY 14260-2900, USA.
Rights and permissions
About this article
Cite this article
Jung, JH. A Note on the Spectral Collocation Approximation of Some Differential Equations with Singular Source Terms. J Sci Comput 39, 49–66 (2009). https://doi.org/10.1007/s10915-008-9249-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-008-9249-x