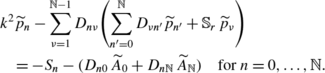Abstract
The anelastic Stokes eigenmodes are computed for a fluid confined, in presence of gravity, between two horizontally infinite plates. These eigenmodes are described by one horizontal wave number k. The eigenvalues λ(k 2) are proved to be all negative. They depend monotonically upon k, behaving like k 2 for very large k.
Two particular values of k are considered, i.e., k=2 π and k=0, and the stratification parameter of the equilibrium state is taken between 0 (incompressible approximation) and 10 (upper limit of the anelastic configuration). The k=2 π eigenvalue problem is solved numerically while the k=0 is solved both numerically and analytically. Two physical configurations are analyzed, one with no-slip boundary conditions imposed on both horizontal walls, and one with no-stress, while imposing no flow through these boundaries in both cases. The main results are: (i) the smaller the stratification, the larger the decay rate, (ii) the eigenmodes are localized in the lower part of the channel, their vertical extension increasing with the eigenmode spatial frequency, (iii) the Neumann eigenmode decay rates are smaller than their Dirichlet counterparts, except for k=0, where it is just the reverse, (iv) a general trend seems to emerge from the present study, regarding the way the numerical eigenvalues of an elliptic operator compare with the analytical ones, viz., the numerical spectrum overestimates (in absolute value) the analytical spectrum, slightly in the low frequency part of the spectrum and more and more strongly in the upper part.














We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.
References
Abarzhi, S.I., Gauthier, S., Rosner, R.: Preface: turbulent mixing and beyond. In: 1st International Conference on Turbulent Mixing and Beyond, vol. T132, pp. 011001–014056 (2009)
Abarzhi, S.I., Sreenvivasan, K.R.: Introduction: turbulent mixing and beyond. Philos. Trans. R. Soc. Lond. A, 368, 1537–1828 (2010). 1st International Conference on Turbulent Mixing and Beyond
Batoul, A., Khallouf, H., Labrosse, G.: Une méthode de résolution directe (pseudo-spectrale) du problème de Stokes 2D/3D instationnaire. Application à la cavité entrainée carrée. C. R. Acad. Sci. Paris, Ser. II 319, 1455–1461 (1994)
Brenier, B., Roux, B., Bontoux, P.: Comparaison des méthodes Tau-Chebyshev et Galerkin dans l’étude de stabilité des mouvements de convection naturelle. Problème des valeurs propres parasites. J. Méc. Théor. Appl. 5(1), 95–119 (1986)
Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods in Fluid Dynamics. Springer Series in Computational Physics. Springer, New York (1988)
Chu, B.-T., Kovásznay, L.S.G.: Non-linear interactions in a viscous heat-conducting compressible gas. J. Fluid Mech. 3, 494–514 (1957)
Gary, J., Helgason, R.: A matrix method for the ordinary differential eigenvalue problem. J. Comput. Phys. 5, 169–187 (1970)
Gough, D.O.: The anelastic approximation for thermal convection. J. Atmos. Sci. 26, 448–456 (1969)
Harris, D.L., Reid, W.H.: On orthogonal functions which satisfy four boundary conditions. I. Tables for use in Fourier-type expansions. Astrophys. J. Suppl. Ser. 3, 429–447 (1958)
Labrosse, G.: The piecewise-linear Finite Volume scheme: the best known lowest-order preconditioner for the \(\frac{d^{2}}{dx^{2}}\) Chebyshev spectral operator. J. Comput. Phys. 228(12), 4491–4509 (2009)
Le Creurer, B., Gauthier, S.: A return toward equilibrium in a two-dimensional Rayleigh-Taylor instability for compressible miscible fluids. Theor. Comput. Fluid Dyn. 22, 125–144 (2008)
Leriche, E., Labrosse, G.: High-order direct Stokes solvers with or without temporal splitting: numerical investigations of their comparative properties. SIAM J. Sci. Comput. 22, 1386–1410 (2000)
Leriche, E., Labrosse, G.: Stokes eigenmodes in square domain and the stream function—vorticity correlation. J. Comput. Phys. 200, 489–511 (2004)
Leriche, E., Labrosse, G.: Vector potential—vorticity relationship for the Stokes flows: application to the Stokes eigenmodes in 2D/3D closed domain. Theor. Comput. Fluid Dyn. 21(1), 1–13 (2007)
Malik, M.R.: Numerical methods for hypersonic boundary layers stability. J. Comput. Phys. 86, 376–413 (1990)
Malik, M.R., Orszag, S.A.: Linear stability analysis of three-dimensional compressible boundary layers. J. Sci. Comput. 2(1), 77–97 (1987)
Orszag, S.A., Israeli, M., Deville, M.: Boundary conditions for incompressible flows. J. Sci. Comput. 1(1), 75–111 (1986)
Råde, L., Westergren, B.: Mathematics Handbook for Science and Engineering. Springer, Berlin (1999)
Reid, W.H., Harris, D.L.: On orthogonal functions which satisfy four boundary conditions. II. Integrals for use with Fourier-type expansions. Astrophys. J. Suppl. Ser. 3, 448–452 (1958)
Vandeven, H.: On the eigenvalues of second-order spectral differentiation operators. Comput. Methods Appl. Mech. Eng. 80, 313–318 (1990)
Wolfram, S.: The Mathematica Book, Fourth edn. Wolfram Media/Cambridge University Press, Cambridge (1999)
Zebib, A.: A Chebyshev method for the solution of boundary value problems. J. Comput. Phys. 53, 443–455 (1984)
Zebib, A.: Removal of spurious modes encountered in solving stability problems by spectral methods. J. Comput. Phys. 70, 521–525 (1987)
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: The Pressure Discrete System
In most of the closed flows the pressure is not known on the boundaries and the \(\vec{\nabla}^{2}p\) equation (see (28) for example) it must verify cannot be used for determining it. This is one aspect of the (\(\vec{\mathbf{v}}\), p) uncoupling in the incompressible and anelastic formulations of the Navier-Stokes problem. The present case is fairly easy to treat: the x-periodicity of the configuration leads to separate equations on the velocity and pressure fields. Once the velocity is known the pressure remains to be determined without introducing any boundary condition. To this end we use the Projection-Diffusion approach, [3, 12], which turns out to be the only spectrally accurate numerical tool capable of computing the Stokes eigenmodes in the cube, [14]. It will lead to a discrete system which is very close to (28) but does not require to be completed by boundary conditions for being inverted. Let us see the way we proceed.
The right-hand side of (28) is considered as being analytically known, which is practically the case from (43) and (45). We can therefore compute its nodal values at any given set of points. These points are chosen to be located at the Chebyshev Gauss-Lobatto (CGL) coordinates, [5],
where ℕ is the Chebyshev cut-off of the decomposition of the field \(\widetilde{p}(z)\). Let us introduce the column vector \(\widetilde{P}\) made of the (ℕ+1) CGL nodal values of \(\widetilde{p}(z)\), i.e.,
Let D be the first-derivation CGL matrix, of size (ℕ+1), whose entries are given by
where
We can now discretize Eq. (36) and, then, take into account both the right part of (35) and the boundary conditions (37) or (38). This leads to a three-step handling.
-
1.
One has directly, from (36),
$$ ik (\widetilde{a}_x )_n+\sum_{n'=0}^{\mathbb{N}}D_{nn'} (\widetilde{a}_z)_{n'} =-S_n\quad \hbox{for} \ n=0,\ldots,\mathbb{N}, $$(47)where \((\widetilde{a}_{x} )_{n}\) and \((\widetilde{a}_{z} )_{n}\) are the nodal values of \(\widetilde{a}_{x}\) and \(\widetilde{a}_{z}\) at z=z n and
$$S_n=\frac{4}{3}\mathbb{S}_r\biggl(\frac{d^2}{dz^2}-k^2 \biggr)\widetilde{w} \bigg\vert_{z_n} $$supplies the nodal value at z=z n of the right-hand side of Eq. (36).
-
2.
The boundary values, \((\widetilde{a}_{z} )_{0}\) and \((\widetilde{a}_{z} )_{\mathbb{N}}\), of \(\widetilde{a}_{z}\) are imposed by (37) or (38). Lets denote them by
$$(\widetilde{a}_z )_{\bullet}=\widetilde{A}_{\bullet} \quad \hbox{with} \ \bullet=0,\mathbb{N}. $$They can thus be introduced in (47) which leads to
$$ik (\widetilde{a}_x )_n+\sum _{\nu=1}^{\mathbb{N}-1}D_{n\nu} (\widetilde{a}_z )_{\nu}=-S_n- (D_{n0}\,\widetilde {A}_{0}+D_{n\mathbb{N}}\,\widetilde{A}_{\mathbb{N}} ) \quad \hbox{for} \ n=0,\ldots ,\mathbb{N}. $$ -
3.
The remaining nodal values of \(\widetilde{a}_{x}\) and \(\widetilde{a}_{z}\) are replaced in this latter equation by the right part of (35). This introduces the pressure nodal values, according to
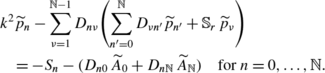
This is the pressure equation which can be given a matrix form, by introducing rectangular matrices, i.e., \(\overline{D}\) of (ℕ+1) rows and (ℕ−1) columns and \(\underline{D}\) of (ℕ−1) rows and (ℕ+1) columns, their entries being thus such that
and
Whence the pressure discrete system,
where I is the unit matrix of size (ℕ+1), \(\underline{I}\) its restriction to (ℕ−1) rows, and \(\widetilde{S}\) is the vector column made of the (ℕ+1) quantities \((S_{n}+ (D_{n0}\,\widetilde{A}_{0}+D_{n\mathbb{N}}\,\widetilde{A}_{\mathbb{N}} ) )\), i.e., for n=0,…,ℕ. It is instructive to compare (28) with (48). The latter equation is the closest discrete version of the former which does not require any boundary condition to be inverted. In particular, the matrix \(\overline{D}\cdot \underline{D}\), called the quasi-\(\frac{d^{2}}{dz^{2}}\) operator, has real eigenvalues, all negative except two of them which are zero. It is the elementary brick of the quasi-Poisson operator which determines the pressure in the incompressible context, [12].
Appendix B: Extended Reid-Harris Functions \(\varPhi^{\mathrm{(N)}}(\alpha;z)\)
These eigenfunctions are defined by Eqs. (39) and (41). Their boundary conditions do not allow them to enjoy any z-symmetry property. We can therefore express them as a linear combination of the z-even and -odd RH eigenfunctions, i.e.,
where the coefficient β has to be related to the eigenvalue α. Each z-even and -odd part of \(\varPhi^{\mathrm{(N)}}(z)\) satisfies the differential equation (39) and the Dirichlet part of the boundary condition (41). One thus has only to impose the mixed boundary condition, viz., the left-hand side of (41). It supplies
the eigenvalues α being the roots of the following transcendental equation,
Like the RH functions, the \(\varPhi^{\mathrm{(N)}}(\alpha;z)\) are orthogonal, but not normalized, by the following scalar product,
where \(\sqrt{\mathbb{L}(\alpha_{n} )}\) is the L 2 norm of \(\varPhi^{\mathrm{(N)}}(\alpha_{n};z)\). In Table 4 are given the 10 leading eigenvalues α together with the associated β’s and \(\mathbb{L}(\alpha_{n} )\)’s, obtained for \(\mathbb{S}_{r}=5\). The data are given with 16 significant digits.
Appendix C: The Incompressible Stokes Eigenmodes in Infinite Channel
This appendix is devoted to the case where \(\mathbb{S}_{r}=0\), i.e., when the rest state is of constant density and the flow is therefore taken as incompressible. The pressure equation obtains from (28) and (16). It reads
For the velocity vertical component \(\widetilde{w}\), one had (32), recalled here
completed by the boundary conditions, in Case (D),
and, in Case (N),
In both cases, the Stokes eigenmodes \(\widetilde{w}(z)\) enjoy a z-symmetry property: they are either symmetrical or anti-symmetrical under the mirror operation z→−z. The associated eigenmodes are denoted by \(\widetilde{w}_{e}(z)\) and \(\widetilde{w}_{o}(z)\).
The Case (D), no-slip on the top and bottom walls, is well known, [14, 17]. We just give here its analytical description. The velocity components \(\widetilde{w}_{e}(z)\) and \(\widetilde{w}_{o}(z)\) read
where the μ e ’s and μ o ’s are the roots of the following transcendental relations
The corresponding Stokes eigenvalues are given by \(\lambda_{\bullet}=-(k^{2}+\mu_{\bullet}^{2})\) with •=e,o. The first eigenvalues are listed in [17] for k=1,10.
The Case (N), no-stress on the top and bottom walls, defined by (51) and (52), becomes periodic in z, with
where
The Stokes eigenvalues are then simply \(\lambda(n)=- (k^{2}+ (n\, \frac{\pi}{2} )^{2} )\) for n=1,…,∞. The associated dynamical pressure field is harmonic by (50). It has also to be periodic in all space directions. It must then be zero, \(\widetilde{p}(z)=0\).
Rights and permissions
About this article
Cite this article
Hammouch, Z., Labrosse, G. & Gauthier, S. Anelastic Stokes Eigenmodes in Infinite Channel. J Sci Comput 55, 65–91 (2013). https://doi.org/10.1007/s10915-012-9622-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-012-9622-7