Strong Stability for Runge–Kutta Schemes on a Class of Nonlinear Problems

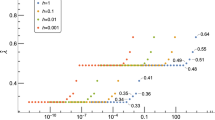
Abstract

In this paper we consider Strong Stability Preserving (SSP) properties for explicit Runge–Kutta (RK) methods applied to a class of nonlinear ordinary differential equations. We define new modified threshold factors that allow us to prove properties, provided that they hold for explicit Euler steps. For many methods, the stepsize restrictions obtained are sharper than the ones obtained in terms of the Kraaijevanger’s coefficient in the SSP theory. In particular, for the classical 4-stage fourth order method we get nontrivial stepsize restrictions. Furthermore, the order barrier $p\le 4$ for explicit SSP RK methods is not obtained. An open question is the existence of explicit RK schemes with order $p\ge 5$ and nontrivial modified threshold factor. The numerical experiments done illustrate the results obtained.

Appendix

In this section we give the coefficients of several explicit methods from the literature used in the numerical experiments.

Methods (6.2-b) and (6.3-b) are the optimal $s$ stage order $s$ explicit RK methods with $\mathcal{R}(\mathbb A )=1$. Methods (6.2a, b) and (6.3a, b) have been used in [12] in the context of positivity; methods (6.2c, d) and (6.3c, d) have been used in [27].

• First order method:

  $$\begin{aligned} \begin{array}{c|cc} 0 &{} 0 &{} \\ \frac{3}{4} &{} \frac{3}{4} &{} 0 \\ \hline &{} 0 &{} 1 \end{array} \end{aligned}$$

  (6.1)

• Second order methods:

  $$\begin{aligned} \begin{array}{ll} \text{(a) } \quad \quad \begin{array}{c|cc} 0 &{} 0 &{} \\ \frac{1}{2} &{} \frac{1}{2} &{} 0 \\ \hline &{} 0 &{} 1 \end{array} &{} \text{(b) } \quad \quad \begin{array}{c|cc} 0 &{} 0 &{} \\ 1 &{} 1 &{} 0 \\ \hline &{} \frac{1}{2} &{} \frac{1}{2}\\ \end{array}\\ \text{(c) } \quad \quad \begin{array}{c|ccc} 0 &{} 0 &{} &{}\\ \frac{1}{3} &{} \frac{1}{3} &{} 0 &{} \\ 1 &{} 0 &{} 1 &{} 0 \\ \hline &{} \frac{1}{2} &{} 0 &{} \frac{1}{2} \end{array} &{} \text{(d) } \quad \quad \begin{array}{l|llll} 0 &{} 0 &{} &{} &{} \\ \frac{2}{3} &{}\frac{2}{3} &{} 0 &{} &{} \\ \frac{2}{3} &{}0 &{} \frac{2}{3} &{} 0 &{} \\ \frac{2}{3} &{}0 &{} 0 &{} \frac{2}{3} &{} 0\\ \hline &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} &{} \frac{1}{4} \end{array} \end{array} \end{aligned}$$

  (6.2)

• Third order methods

  $$\begin{aligned} \begin{array}{ll} \text{(a) } \quad \quad \begin{array}{c|ccc} 0 &{} 0 &{} &{} \\ \frac{1}{3} &{} \frac{1}{3} &{} 0 &{} \\ \frac{2}{3} &{} 0 &{} \frac{2}{3} &{} 0 \\ \hline &{} \frac{1}{4} &{} 0 &{} \frac{3}{4} \end{array} &{} \text{(b) } \quad \quad \begin{array}{c|ccc} 0 &{} 0 &{} &{} \\ 1 &{} 1 &{} 0 &{} \\ \frac{1}{2} &{} \frac{1}{4} &{} \frac{1}{4} &{} 0 \\ \hline &{} \frac{1}{6} &{} \frac{1}{6} &{} \frac{2}{3}\\ \end{array} \\ \text{(c) } \quad \quad \begin{array}{c|ccc} 0 &{} 0 &{} &{} \\ -\frac{4}{9} &{} -\frac{4}{9} &{} 0 &{} \\ \frac{2}{3} &{} \frac{7}{6} &{} -\frac{1}{2} &{} 0 \\ \hline &{} \frac{1}{4} &{} 0 &{} \frac{1}{4} \end{array} &{} \text{(d) } \quad \quad \begin{array}{c|ccccc} 0 &{} 0 &{} &{} &{} &{} \\ \frac{1}{7} &{} \frac{1}{7} &{} 0 &{} &{} &{}\\ \frac{3}{16} &{} 0 &{} \frac{3}{16} &{} 0 &{} &{} \\ \frac{1}{3} &{} 0 &{} 0 &{} \frac{1}{3} &{} 0 &{} \\ \frac{2}{3} &{} 0 &{} 0 &{} 0 &{} \frac{2}{3} &{} 0\\ \hline &{} \frac{1}{4} &{} 0 &{} 0 &{} 0 &{} \frac{3}{4} \end{array} \end{array} \end{aligned}$$

  (6.3)