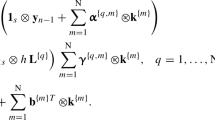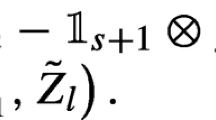Skip to main content
SpringerLink
Log in

A Linearly Fourth Order Multirate Runge–Kutta Method with Error Control

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

To integrate large systems of locally coupled ordinary differential equations with disparate timescales, we present a multirate method with error control that is based on the Cash–Karp Runge–Kutta formula. The order of multirate methods often depends on interpolating certain solution components with a polynomial of sufficiently high degree. By using cubic interpolants and analyzing the method applied to a simple test equation, we show that our method is fourth order linearly accurate overall. Furthermore, the size of the region of absolute stability is increased when taking many “micro-steps” within a “macro-step.” Finally, we demonstrate our method on three simple test problems to confirm fourth order convergence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. We use the word “interpolation” to describe a method to construct a smooth approximation to the numerical solution between two times \(t_n\) and \(t_{n+1}\). However, the function that we derive does not pass through the numerical solution at \(t_{n+1}\). Strictly speaking, it is not an interpolant. Nevertheless, we still refer to these approximating functions as “interpolants.”

References

  1. Andrus, J.F.: Numerical solution of systems of ordinary differential equations separated into subsystems. SIAM J. Numer. Anal. 16, 605–611 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bartel, A., Günther, M.: A multirate W-method for electrical networks in state-space formulation. J. Comput. Appl. Math. 147(2), 411–425 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bartel, A., Günther, M., Kvaerno, A.: Multirate methods in electrical circuit simulation. Prog. Ind. Math. ECMI 2000, 258–265 (2000)

    Google Scholar 

  4. Constantinescu, E.M., Sandu, A.: Extrapolated multirate methods for differential equations with multiple time scales. J. Sci. Comput. 56(1), 28–44 (2013)

  5. Constantinescu, E.M., Adrian, Sandu: Multirate timestepping methods for hyperbolic conservation laws. J. Sci. Comput. 33, 239–278 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Constantinescu, E.M., Sandu, Adrian: Multirate explicit Adams methods for time integration. J. Sci. Comput. 38, 229–249 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Enright, W.H., Jackson, K.R., Nørsett, S.P., Thomsen, P.G.: Interpolants for Runge–Kutta formulas. ACM Trans. Math. Softw. 12(3), 193–218 (1986)

    Article  MATH  Google Scholar 

  8. Gear, C.W., Wells, D.R.: Multirate linear multistep methods. BIT 24, 484–502 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  9. Günther, M., Kværnø, A., Rentrop, P.: Multirate partitioned Runge–Kutta methods. BIT 41(3), 504–514 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hairer, E., Norsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I: Nonstiff Problems. Springer Series in Computational Mathematics. Springer (1987)

  11. Horn, M.K.: Fourth and fifth order, scaled Runge–Kutta algorithms for treating dense output. SIAM J. Numer. Anal. 20(3), 558–568 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hundsdorfer, W., Savcenco, V.: Analysis of a multirate theta-method for stiff ODEs. Appl. Numer. Math. 59, 693–706 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kato, T., Kataoka, T.: Circuit analysis by a new multirate method. Electr. Eng. Jpn. 126(4), 1623–1628 (1999)

    Article  Google Scholar 

  14. Logg, A.: Multi-adaptive time integration. Appl. Numer. Math. 48, 339–354 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  15. Makino, J., Aarseth, S.: On a Hermite integrator with Ahmad-Cohen scheme for gravitational many-body problems. Publ. Astron. Soc. Japan 44, 141–151 (1992)

    Google Scholar 

  16. Press, W.H., Teukolsky, S.A., Vetterling, W.V., Flannery, B.P.: Numerical Recipes in C: The Art of Scientific Computing, 2nd edn. Cambridge University Press, Cambridge (1992)

    Google Scholar 

  17. Savcenco, V.: Construction of a multirate RODAS method for stiff ODEs. J. Comput. Appl. Math. 225, 323–337 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  18. Savcenco, V., Hundsdorfer, W., Verwer, J.G.: A multirate time stepping strategy for stiff ordinary differential equations. BIT 47, 137–155 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  19. Shampine, L.F.: Some practical Runge-Kutta formulas. Math. Comput. 173, 135–150 (1986)

    Article  MathSciNet  Google Scholar 

  20. Skelboe, S.: Stability properties of backward differentiation multirate formulas. Appl. Numer. Math. 5, 151–160 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  21. Waltz, J., Page, G.L., Milder, S.D., Wallin, J., Antunes, A.: A performance comparison of tree data structures for \({N}\)-body simulation. J. Comput. Phys. 178, 1–14 (2002)

    Article  MATH  Google Scholar 

Download references

Acknowledgments

The author thanks R. R. Rosales who stimulated the author’s interest in multirate methods and proposed the derivation of cubic interpolants.

Author information

Authors and Affiliations

  1. University of Delaware, 412 Ewing Hall, Newark, DE, 19716, USA

    Pak-Wing Fok

Authors
  1. Pak-Wing Fok
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pak-Wing Fok.

Appendix: Matrix Definitions

Appendix: Matrix Definitions

Here we given the definitions of the matrices in Eqs. (17–19).

$$\begin{aligned} L_0= & {} I_{6N_0} + h(A \otimes M_{00}) - h^2 (A \otimes M_{01}) \left[ \varSigma _2(M,hA)\right] ^{-1} (A \otimes M_{10}), \\ L_1= & {} -I_{6N_1} - h(A \otimes M_{11}) + \varSigma _0(M,hA) + \varSigma _2(M,hA), \\ L_2= & {} I_{6N_2} + h(A \otimes M_{22}) - h^2 (A \otimes M_{21}) \left[ \varSigma _0(M,hA)\right] ^{-1} (A \otimes M_{12}), \\ U_{00}= & {} -h (\mathbf {1} \otimes M_{00}) + h^2 (A \otimes M_{01}) \left[ \varSigma _2(M,hA)\right] ^{-1} (\mathbf {1} \otimes M_{10}), \\ U_{01}= & {} -h (\mathbf {1} \otimes M_{01}) + h^2 (A \otimes M_{01}) \left[ \varSigma _2(M,hA) \right] ^{-1} (\mathbf {1}\otimes M_{11}) \nonumber \\&- h^3 (A \otimes M_{01})\left[ \varSigma _2(M,hA)\right] ^{-1} (A\otimes M_{12}) (I_{6N_2}+hA \otimes M_{22})^{-1}(\mathbf {1}\otimes M_{21}), \\ U_{02}= & {} h^2 (A \otimes M_{01}) \left[ \varSigma _2(M,hA)\right] ^{-1} (\mathbf {1}\otimes M_{12}) \nonumber \\&- h^3 (A \otimes M_{01}) \left[ \varSigma _2(M,hA)\right] ^{-1}(A \otimes M_{12}) ( I_{6N_2}+hA\otimes M_{22})^{-1}(\mathbf {1} \otimes M_{22}), \\ U_{10}= & {} -h(\mathbf {1}\otimes M_{10}) + h^2 (A \otimes M_{10})(I_{6N_0} + hA \otimes M_{00})^{-1}(\mathbf {1} \otimes M_{00}), \\ U_{11}= & {} -h (\mathbf {1} \otimes M_{11}) + h^2 (A \otimes M_{10})(I_{6N_0}+hA\otimes M_{00})^{-1}(\mathbf {1} \otimes M_{01}) \\&+ h^2 (A \otimes M_{12}) (I_{6N_2}+hA \otimes M_{22})^{-1}(\mathbf {1}\otimes M_{21}),\\ U_{12}= & {} -h(\mathbf {1}\otimes M_{12}) + h^2 (A \otimes M_{12}) (I_{6N_2}+hA \otimes M_{22})^{-1}(\mathbf {1} \otimes M_{22}).\\ U_{20}= & {} h^2 (A \otimes M_{21}) \left[ \varSigma _0(M,hA) \right] ^{-1}(\mathbf {1}\otimes M_{10}) \\&- h^3 (A \otimes M_{21}) \left[ \varSigma _0(M,hA) \right] ^{-1} (A \otimes M_{10}) (I_{6N_0} + hA \otimes M_{00})^{-1} (\mathbf {1} \otimes M_{00}), \\ U_{21}= & {} -h (\mathbf {1}\otimes M_{21}) + h^2 (A \otimes M_{21}) \left[ \varSigma _0(M,hA) \right] ^{-1} (\mathbf {1} \otimes M_{11}) \\&- h^3(A \otimes M_{21})\left[ \varSigma _0(M,hA) \right] ^{-1} (A\otimes M_{10})(I_{6N_0}+hA\otimes M_{00})^{-1} (\mathbf {1}\otimes M_{01}), \\ U_{22}= & {} -h (\mathbf {1}\otimes M_{22}) + h^2 (A \otimes M_{21})\left[ \varSigma _0(M,hA) \right] ^{-1}(\mathbf {1} \otimes M_{12}) \end{aligned}$$

where for matrices \(Z\) and \(M = \left[ \begin{array}{ccc} M_{00} &{} M_{01} &{} M_{02} \\ M_{10} &{} M_{11} &{} M_{12} \\ M_{20} &{} M_{21} &{} M_{22} \end{array}\right] \), we define

$$\begin{aligned} \varSigma _0(M,Z)= & {} I_{6N_1} + (Z \otimes M_{11}) - (Z \otimes M_{10}) (I_{6N_0}+Z \otimes M_{00})^{-1} (Z \otimes M_{01}),\\ \varSigma _2(M,Z)= & {} I_{6N_1} + (Z \otimes M_{11}) - (Z \otimes M_{12}) (I_{6N_2}+Z \otimes M_{22})^{-1} (Z \otimes M_{21}). \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fok, PW. A Linearly Fourth Order Multirate Runge–Kutta Method with Error Control. J Sci Comput 66, 177–195 (2016). https://doi.org/10.1007/s10915-015-0017-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-015-0017-4

Keywords

Search

Navigation