A New Mapped Weighted Essentially Non-oscillatory Method Using Rational Mapping Function

Abstract

In this paper, we develop a new mapped weighted essentially non-oscillatory method for hyperbolic conservation laws by proposing a new family of mapping functions, which includes the mapping function in Henrick et al. (J Comput Phys 207:542–567, 2005) as one of its members. The new family of mapping functions has three parameters, namely m, n and k. When it is applied to the $(2r-1)$-th-order WENO-JS methods, $r=3$, 4, 5 and 6, it is well defined and monotonically increasing with proper choice of m, n and k. Furthermore, it can achieve the optimal order of accuracy at or near critical points in smooth regions with proper choices of n. The new family of mapping functions uses rational functions, thus it is a family of smooth functions (Note that, the mapping function in Feng et al. (J Sci Comput 51:449–473, 2012) is only piecewise continuous). Among the new family of mapping functions, the new mapping function with $(m,n,k)=(2,6,0)$ has the best performance (i.e., no matter for short time or for long time simulations, it provides the more accurate numerical solutions).

Appendices

Appendix 1

Table 12 is used in the verification of Property 1, Table 13 is used in Remark 3, and Table 14 is used in Theorem 2.

Table 12 The roots of P(x) with different $d_i$ used in fifth-order WENO-RM(mn0)

Table 13 The values of $b_m$ and $b_{m+1}+b_m$ in the fifth-order WENO-RM(mn0) method

Table 14 The roots of P(x) with different $d_i$ used in fifth-order WENO-RM(mn1)

Appendix 2

In this Appendix we first describe a way to write the smoothness indicator, ${\text {IS}}_i^r$, into a positive semi-definite quadratic form. Then we will show that the positive semi-definite quadratic form for computing ${\text {IS}}_i^r$ does improve the accuracy of numerical solutions for some WENO methods, specially for long time simulations.

Clearly, the form of ${\text {IS}}_i^3$ in [15], which is (8), is in a positive semi-definite quadratic form. However, the form of ${\text {IS}}_i^r$ in [2], $r>3$, is not, thus may lead to negative values due to roundoff errors. When negative values of ${\text {IS}}^r_i$ arise, the wrong information may be propagated to the weights. Thus the numerical solutions may be contaminated, and a loss of accuracy can be observed. We now demonstrate a way to convert ${\text {IS}}^r_i$ in [2] into a positive semi-definite quadratic form.

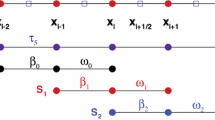
In the $(2r-1)$-th-order WENO method, the interpolation polynomial $p_i(x)$ defined on stencil $S_i$ is of degree $(r-1)$. Define

$$\begin{aligned} p_i(x)=a_0+a_1x+\cdots +a_{r-1}x^{r-1}, \end{aligned}$$

(59)

where $a_j$, $j=0$, 1, $\ldots$, $r-1$, are constants will be determined later. Substituting (59) into (48), a simple calculation leads to the following results.

$$\begin{aligned} {\text {IS}}_i^3= & {} (a_1-a_2)^2+\frac{13}{3}a_2^2, \nonumber \\ {\text {IS}}_i^4= & {} (a_1-a_2+a_3)^2+\frac{13}{3}\left( a_2-\frac{3}{2}a_3\right) ^2+\frac{781}{20}a_3^2, \nonumber \\ {\text {IS}}_i^5= & {} (a_1-a_2+a_3-a_4)^2+\frac{13}{3}\left( a_2-\frac{3}{2}a_3+\frac{129}{65}a_4\right) ^2\nonumber \\&+\frac{781}{20}(a_3-2a_4)^2+\frac{1421461}{2275}a_4^2, \nonumber \\ {\text {IS}}_i^6= & {} (a_1-a_2+a_3-a_4+a_5)^2+\frac{13}{3}\left( a_2-\frac{3}{2}a_3+\frac{129}{65}a_4-\frac{32}{13}a_5\right) ^2\nonumber \\&+\frac{781}{20}\left( a_3-2a_4+\frac{18080}{5467}a_5\right) ^2+ \frac{1421461}{2275}\left( a_4-\frac{5}{2}a_5\right) ^2+\frac{21520059541}{1377684}a_5^2.\nonumber \\ \end{aligned}$$

(60)

Substituting the explicit forms of $a_i$ into (60), we have

${\text {IS}}^3$:

$$\begin{aligned} \begin{array}{l} {\text {IS}}^3_2=\left( \frac{1}{2}u_{j-2}-2u_{j-1}+\frac{3}{2}u_{j}\right) ^2+\frac{13}{3}\left( \frac{1}{2}u_{j-2}-u_{j-1}+\frac{1}{2}u_{j}\right) ^2,\\ {\text {IS}}^3_1=\left( \frac{1}{2}u_{j-1}-\frac{1}{2}u_{j+1}\right) ^2+\frac{13}{3}\left( \frac{1}{2}u_{j-1}-u_{j}+\frac{1}{2}u_{j+1}\right) ^2,\\ {\text {IS}}^3_0=\left( \frac{3}{2}u_{j}-2u_{j+1}+\frac{1}{2}u_{j+2}\right) ^2+\frac{13}{3}\left( \frac{1}{2}u_{j}-u_{j+1}+\frac{1}{2}u_{j+2}\right) ^2, \end{array} \end{aligned}$$

(61)

where ${\text {IS}}^3_i$ is equal to ${\text {IS}}^3_i$ in [15], $i=2$, 1 and 0; ${\text {IS}}^4$:

$$\begin{aligned} \begin{array}{l} {\text {IS}}^4_3=\left( \frac{1}{3}u_{j-3}-\frac{3}{2}u_{j-2}+3u_{j-1}-\frac{11}{6}u_{j}\right) ^2+\frac{13}{3}\left( \frac{1}{2}u_{j-3}-2u_{j-2}+\frac{5}{2}u_{j-1}-u_{j}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{1}{6}u_{j-3}-\frac{1}{2}u_{j-2}+\frac{1}{2}u_{j-1}-\frac{1}{6}u_{j}\right) ^2,\\ {\text {IS}}^4_2=\left( \frac{1}{6}u_{j-2}-u_{j-1}+\frac{1}{2}u_{j}+\frac{1}{3}u_{j+1}\right) ^2+\frac{13}{3}\left( \frac{1}{2}u_{j-1}-u_{j}+\frac{1}{2}u_{j+1}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{1}{6}u_{j-2}-\frac{1}{2}u_{j-1}+\frac{1}{2}u_{j}-\frac{1}{6}u_{j+1}\right) ^2,\\ {\text {IS}}^4_1=\left( \frac{1}{3}u_{j-1}+\frac{1}{2}u_{j}-u_{j+1}+\frac{1}{6}u_{j+2}\right) ^2+\frac{13}{3}\left( \frac{1}{2}u_{j-1}-u_{j}+\frac{1}{2}u_{j+1}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{1}{6}u_{j-1}-\frac{1}{2}u_{j}+\frac{1}{2}u_{j+1}-\frac{1}{6}u_{j+2}\right) ^2,\\ {\text {IS}}^4_0=\left( \frac{11}{6}u_{j}-3u_{j+1}+\frac{3}{2}u_{j+2}-\frac{1}{3}u_{j+3}\right) ^2+\frac{13}{3}\left( u_{j}-\frac{5}{2}u_{j+1}+2u_{j+2}-\frac{1}{2}u_{j+3}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{1}{6}u_{j}-\frac{1}{2}u_{j+1}+\frac{1}{2}u_{j+2}-\frac{1}{6}u_{j+3}\right) ^2, \end{array} \end{aligned}$$

(62)

where ${\text {IS}}^4_i$ is equal to $\frac{1}{240}{\text {IS}}^4_i$ in [2], $i=0,\ldots ,3$

${\text {IS}}^5$:

$$\begin{aligned} \begin{array}{l} {\text {IS}}^5_4=\left( \frac{1}{4}u_{j-4}-\frac{4}{3}u_{j-3}+3u_{j-2}-4u_{j-1}+\frac{25}{12}u_{j}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{119}{260}u_{j-4}-\frac{303}{130}u_{j-3}+\frac{617}{130}u_{j-2}-\frac{563}{130}u_{j-1}+\frac{379}{260}u_{j}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{1}{4}u_{j-4}-\frac{7}{6}u_{j-3}+2u_{j-2}-\frac{3}{2}u_{j-1}+\frac{5}{12}u_{j}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}(\frac{1}{24}u_{j-4}-\frac{1}{6}u_{j-3}+\frac{1}{4}u_{j-2}-\frac{1}{6}u_{j-1}+\frac{1}{24}u_{j})^2,\\ {\text {IS}}^5_3=\left( \frac{1}{12}u_{j-3}-\frac{1}{2}u_{j-2}+\frac{3}{2}u_{j-1}-\frac{5}{6}u_{j}-\frac{1}{4}u_{j+1}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{11}{260}u_{j-3}-\frac{11}{65}u_{j-2}-\frac{16}{65}u_{j-1}+\frac{54}{65}u_{j}-\frac{119}{260}u_{j+1}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{1}{12}u_{j-3}-\frac{1}{2}u_{j-2}+u_{j-1}-\frac{5}{6}u_{j}+\frac{1}{4}u_{j+1}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{24}u_{j-3}-\frac{1}{6}u_{j-2}+\frac{1}{4}u_{j-1}-\frac{1}{6}u_{j}+\frac{1}{24}u_{j+1}\right) ^2,\\ {\text {IS}}^5_2=\left( \frac{1}{12}u_{j-2}-\frac{2}{3}u_{j-1}+\frac{2}{3}u_{j+1}-\frac{1}{12}u_{j+2}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{11}{260}u_{j-2}-\frac{87}{130}u_{j-1}+\frac{163}{130}u_{j}-\frac{87}{130}u_{j+1}+\frac{11}{260}u_{j+2}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{1}{12}u_{j-2}-\frac{1}{6}u_{j-1}+\frac{1}{6}u_{j+1}-\frac{1}{12}u_{j+2}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{24}u_{j-2}-\frac{1}{6}u_{j-1}+\frac{1}{4}u_{j}-\frac{1}{6}u_{j+1}+\frac{1}{24}u_{j+2}\right) ^2,\\ {\text {IS}}^5_1=\left( \frac{1}{4}u_{j-1}+\frac{5}{6}u_{j}-\frac{3}{2}u_{j+1}+\frac{1}{2}u_{j+2}-\frac{1}{12}u_{j+3}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{119}{260}u_{j-1}-\frac{54}{65}u_{j}+\frac{16}{65}u_{j+1}+\frac{11}{65}u_{j+2}-\frac{11}{260}u_{j+3}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{1}{4}u_{j-1}-\frac{5}{6}u_{j}+u_{j+1}-\frac{1}{2}u_{j+2}+\frac{1}{12}u_{j+3}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{24}u_{j-1}-\frac{1}{6}u_{j}+\frac{1}{4}u_{j+1}-\frac{1}{6}u_{j+2}+\frac{1}{24}u_{j+3}\right) ^2,\\ {\text {IS}}^5_0=(\frac{25}{12}u_{j}-4u_{j+1}+3u_{j+2}-\frac{4}{3}u_{j+3}+\frac{1}{4}u_{j+4})^2\\ \qquad \quad +\frac{13}{3}\left( \frac{379}{260}u_{j}-\frac{563}{130}u_{j+1}+\frac{617}{130}u_{j+2}-\frac{303}{130}u_{j+3}+\frac{119}{260}u_{j+4}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{5}{12}u_{j}-\frac{3}{2}u_{j+1}+2u_{j+2}-\frac{7}{6}u_{j+3}+\frac{1}{4}u_{j+4}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{24}u_{j}-\frac{1}{6}u_{j+1}+\frac{1}{4}u_{j+2}-\frac{1}{6}u_{j+3}+\frac{1}{24}u_{j+4}\right) ^2, \end{array} \end{aligned}$$

(63)

where ${\text {IS}}^5_i$ is equal to $\frac{1}{5040}{\text {IS}}^5_i$ in [2], $i=0,\ldots ,4$.

${\text {IS}}^6$:

$$\begin{aligned} \begin{array}{l} {\text {IS}}^6_5=\left( \frac{1}{5}u_{j-5}-\frac{5}{4}u_{j-4}+\frac{10}{3}u_{j-3}-5u_{j-2}+5u_{j-1}-\frac{137}{60}u_{j}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{27}{65}u_{j-5}-\frac{659}{260}u_{j-4}+\frac{843}{130}u_{j-3}-\frac{89}{10}u_{j-2}+\frac{833}{130}u_{j-1}-\frac{487}{260}u_{j}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{114721}{393624}u_{j-5}-\frac{672011}{393624}u_{j-4}+\frac{803219}{196812}u_{j-3}-\frac{967229}{196812}u_{j-2}+\frac{1164041}{393624}u_{j-1}-\frac{278731}{393624}u_{j}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{12}u_{j-5}-\frac{11}{24}u_{j-4}+u_{j-3}-\frac{13}{12}u_{j-2}+\frac{7}{12}u_{j-1}-\frac{1}{8}u_{j}\right) ^2\\ \qquad \quad +\frac{21520059541}{1377684}\left( \frac{1}{120}u_{j-5}-\frac{1}{24}u_{j-4}+\frac{1}{12}u_{j-3}-\frac{1}{12}u_{j-2}+\frac{1}{24}u_{j-1}-\frac{1}{120}u_{j}\right) ^2,\\ {\text {IS}}^6_4=\left( \frac{1}{20}u_{j-4}-\frac{1}{3}u_{j-3}+u_{j-2}-2u_{j-1}+\frac{13}{12}u_{j}+\frac{1}{5}u_{j+1}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{11}{260}u_{j-4}-\frac{33}{130}u_{j-3}+\frac{77}{130}u_{j-2}-\frac{23}{130}u_{j-1}-\frac{161}{260}u_{j}+\frac{27}{65}u_{j+1}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{16315}{393624}u_{j-4}-\frac{114377}{393624}u_{j-3}+\frac{179981}{196812}u_{j-2}-\frac{278387}{196812}u_{j-1}+\frac{409595}{393624}u_{j}-\frac{114721}{393624}u_{j+1}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{24}u_{j-4}-\frac{1}{4}u_{j-3}+\frac{7}{12}u_{j-2}-\frac{2}{3}u_{j-1}+\frac{3}{8}u_{j}-\frac{1}{12}u_{j+1}\right) ^2\\ \qquad \quad +\frac{21520059541}{1377684}\left( \frac{1}{120}u_{j-4}-\frac{1}{24}u_{j-3}+\frac{1}{12}u_{j-2}-\frac{1}{12}u_{j-1}+\frac{1}{24}u_{j}-\frac{1}{120}u_{j+1}\right) ^2,\\ {\text {IS}}^6_3=\left( \frac{1}{30}u_{j-3}-\frac{1}{4}u_{j-2}+u_{j-1}-\frac{1}{3}u_{j}-\frac{1}{2}u_{j+1}+\frac{1}{20}u_{j+2}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{11}{260}u_{j-2}-\frac{87}{130}u_{j-1}+\frac{163}{130}u_{j}-\frac{87}{130}u_{j+1}+\frac{11}{260}u_{j+2}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{16487}{393624}u_{j-3}-\frac{115237}{393624}u_{j-2}+\frac{115237}{196812}u_{j-1}-\frac{82435}{196812}u_{j}+\frac{16831}{393624}u_{j+1}+\frac{16315}{393624}u_{j+2}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{24}u_{j-2}-\frac{1}{6}u_{j-1}+\frac{1}{4}u_{j}-\frac{1}{6}u_{j+1}+\frac{1}{24}u_{j+2}\right) ^2\\ \qquad \quad +\frac{21520059541}{1377684}\left( \frac{1}{120}u_{j-3}-\frac{1}{24}u_{j-2}+\frac{1}{12}u_{j-1}-\frac{1}{12}u_{j}+\frac{1}{24}u_{j+1}-\frac{1}{120}u_{j+2}\right) ^2,\\ {\text {IS}}^6_2=\left( \frac{1}{20}u_{j-2}-\frac{1}{2}u_{j-1}-\frac{1}{3}u_{j}+u_{j+1}-\frac{1}{4}u_{j+2}+\frac{1}{30}u_{j+3}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{11}{260}u_{j-2}-\frac{87}{130}u_{j-1}+\frac{163}{130}u_{j}-\frac{87}{130}u_{j+1}+\frac{11}{260}u_{j+2}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{16315}{393624}u_{j-2}+\frac{16831}{393624}u_{j-1}-\frac{82435}{196812}u_{j}+\frac{115237}{196812}u_{j+1}-\frac{115237}{393624}u_{j+2}+\frac{16487}{393624}u_{j+3}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{24}u_{j-2}-\frac{1}{6}u_{j-1}+\frac{1}{4}u_{j}-\frac{1}{6}u_{j+1}+\frac{1}{24}u_{j+2}\right) ^2\\ \qquad \quad +\frac{21520059541}{1377684}\left( \frac{1}{120}u_{j-2}-\frac{1}{24}u_{j-1}+\frac{1}{12}u_{j}-\frac{1}{12}u_{j+1}+\frac{1}{24}u_{j+2}-\frac{1}{120}u_{j+3}\right) ^2,\\ {\text {IS}}^6_1=\left( \frac{1}{5}u_{j-1}+\frac{13}{12}u_{j}-2*u_{j+1}+u_{j+2}-\frac{1}{3}u_{j+3}+\frac{1}{20}u_{j+4}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{27}{65}u_{j-1}-\frac{161}{260}u_{j}-\frac{23}{130}u_{j+1}+\frac{77}{130}u_{j+2}-\frac{33}{130}u_{j+3}+\frac{11}{260}u_{j+4}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{114721}{393624}u_{j-1}-\frac{409595}{393624}u_{j}+\frac{278387}{196812}u_{j+1}-\frac{179981}{196812}u_{j+2}+\frac{114377}{393624}u_{j+3}-\frac{16315}{393624}u_{j+4}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{12}u_{j-1}-\frac{3}{8}u_{j}+\frac{2}{3}u_{j+1}-\frac{7}{12}u_{j+2}+\frac{1}{4}u_{j+3}-\frac{1}{24}u_{j+4}\right) ^2\\ \qquad \quad +\frac{21520059541}{1377684}\left( \frac{1}{120}u_{j-1}-\frac{1}{24}u_{j}+\frac{1}{12}u_{j+1}-\frac{1}{12}u_{j+2}+\frac{1}{24}u_{j+3}-\frac{1}{120}u_{j+4}\right) ^2,\\ {\text {IS}}^6_0=\left( \frac{137}{60}u_{j}-5u_{j+1}+5u_{j+2}-\frac{10}{3}u_{j+3}+\frac{5}{4}u_{j+4}-\frac{1}{5}u_{j+5}\right) ^2\\ \qquad \quad +\frac{13}{3}\left( \frac{487}{260}u_{j}-\frac{833}{130}u_{j+1}+\frac{89}{10}u_{j+2}-\frac{843}{130}u_{j+3}+\frac{659}{260}u_{j+4}-\frac{27}{65}u_{j+5}\right) ^2\\ \qquad \quad +\frac{781}{20}\left( \frac{278731}{393624}u_{j}-\frac{1164041}{393624}u_{j+1}+\frac{967229}{196812}u_{j+2}-\frac{803219}{196812}u_{j+3}+\frac{672011}{393624}u_{j+4}-\frac{114721}{393624}u_{j+5}\right) ^2\\ \qquad \quad +\frac{1421461}{2275}\left( \frac{1}{8}u_{j}-\frac{7}{12}u_{j+1}+\frac{13}{12}u_{j+2}-u_{j+3}+\frac{11}{24}u_{j+4}-\frac{1}{12}u_{j+5}\right) ^2\\ \qquad \quad +\frac{21520059541}{1377684}\left( \frac{1}{120}u_{j}-\frac{1}{24}u_{j+1}+\frac{1}{12}u_{j+2}-\frac{1}{12}u_{j+3}+\frac{1}{24}u_{j+4}-\frac{1}{120}u_{j+5}\right) ^2, \end{array} \end{aligned}$$

(64)

where ${\text {IS}}^6_i$ is equal to $\frac{1}{120960}{\text {IS}}^6_i$ in [2], $i=0,\ldots ,5$.

Remark 7

${\text {IS}}_i^3$ in (61), ${\text {IS}}_i^4$ in (62) and ${\text {IS}}_i^5$ in (63) can be verified to be equal to the ones in the early literature (see Eqs. (9), (15) and (22) in [1]) proposed by Balsara et al.. On the other hand, ${\text {IS}}_i^6$ in (64) does not appear in [1]. Comparing to [1], our work presents different aspects. First, in order to calculate ${\text {IS}}_i^r$ in (48), the interpolation polynomial $p_i(x)$ on stencil $S_i$ needs to be defined, in [1], $p_i(x)$ is defined as the combination of Legendre polynomial basis set. But in our paper, we apply a more natural approach. That is, $p_i(x)$ is defined as the polynomial as in (59). Second, we have demonstrated the relation between the new forms of ${\text {IS}}_i^r$ and the original ones in [2, 15]; i.e., the new forms of ${\text {IS}}^3_i$ is equal to ${\text {IS}}^3_i$ in [15], the new ${\text {IS}}^4_i$ is equal to $\frac{1}{240}{\text {IS}}^4_i$ in [2], the new ${\text {IS}}^5_i$ is equal to $\frac{1}{5040}{\text {IS}}^5_i$ in [2], and the new ${\text {IS}}^6_i$ is equal to $\frac{1}{120960}{\text {IS}}^6_i$ in [2]. Third, we demonstrate that this positive semi-definite quadratic form of ${\text {IS}}_i^r$ does improve the performance of some WENO methods, specially for long time simulations (more details are given as follows).

Now we test the effect of different forms of ${\text {IS}}_i^4$ and ${\text {IS}}_i^5$ by solving the linear advection (50) with periodic boundary conditions, and the initial conditions are set to be

$$\begin{aligned} u(x,0)=\left\{ \begin{array}{ll} 1, &{}\quad x\in [0,1), \\ -1, &{}\quad x\in [1,2). \\ \end{array} \right. \end{aligned}$$

(65)

Four seventh-order and ninth-order WENO methods, i.e., WENO-JS($\epsilon =10^{-6}$), WENO-HAP($\epsilon =10^{-40}$), WENO-PM6($\epsilon =10^{-99}$) and WENO-RM(260)($\epsilon =10^{-99}$), are employed for the test. Set $N=200$, the CFL number is chosen to be 0.1. In order to simplify the notation, we use ${\text {IS}}_i^r$-s to refer the ${\text {IS}}_i^r$ which is not in a positive semi-definite quadratic form, and use ${\text {IS}}_i^r$-ns to refer the ${\text {IS}}_i^r$ which is not in a positive semi-definite quadratic form.

Table 15 Effect of different ${\text {IS}}_i^4$

Table 15 gives the $L_1$-norm error of numerical solutions of four seventh-order WENO methods using different forms of ${\text {IS}}^4_i$. We observe that, for WENO-JS, there is essentially no difference by applying ${\text {IS}}_i^4$-s or ${\text {IS}}_i^4$-ns. For WENO-HAP, the effects by applying different forms of ${\text {IS}}_i^4$ are unable to be observed when $t\le 100$. However, as time evolves, WENO-HAP with ${\text {IS}}_i^4$-s provides more accurate numerical solutions when $t =500$ and 1000. WENO-PM6 and WENO-RM(260) with ${\text {IS}}_i^4$-s provide more accurate numerical solutions than the ones with ${\text {IS}}_i^4$-ns no mater for short time or for long time simulations. Furthermore, as time increases, the improvement is more obvious. Figure 24 gives the plot of the effect by using different ${\text {IS}}_i^4$ at $t =1000$, only the performance by WENO-HAP and WENO-RM(260) is given since the performance by WENO-PM6 is almost identical as the one by WENO-RM(260).

Fig. 24

Effect of different ${\text {IS}}_i^4$

Table 16 Effect of different ${\text {IS}}_i^5$

Fig. 25

Effect of different ${\text {IS}}_i^5$

Fig. 26

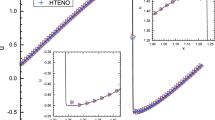
Zoomed graph 1 of Fig. 25

Fig. 27

Zoomed graph 2 of Fig. 25

Table 16 gives the $L_1$-norm errors of numerical solutions of four ninth-order WENO methods using different forms of ${\text {IS}}^5_i$. Comparing WENO-JS with ${\text {IS}}_i^5$-ns, WENO-JS with ${\text {IS}}_i^5$-s gives comparable numerical solutions when $t\,=\,10$ and 50. It gives less accurate solutions when $t\,=\,100$ and 500, but gives more accurate solution when $t\,=\,1000$. For WENO-HAP, the effect by applying different ${\text {IS}}_i^5$ is similar. The WENO-PM6 and WENO-RM(260) methods using ${\text {IS}}_i^5$-s can provide more accurate numerical solutions than the ones using ${\text {IS}}_i^5$-ns no mater for short time or for for long time simulations. Once again, as time evolves, the improvements are more obvious. Figure 25 gives the plot of the effect by using different forms of ${\text {IS}}_i^5$ at $t\,=\,1000$. Only the performance of WENO-PM6 and WENO-RM(260) is given. Figures 26 and 27 are the zoomed graph of Fig. 25. There are interesting observations. First, WENO-PM6 using ${\text {IS}}_i^5$-ns generates lots of the oscillations, while WENO-PM6 using ${\text {IS}}_i^5$-s reduces the oscillations greatly. Second, WENO-RM(260) using ${\text {IS}}_i^5$-ns also generates some oscillations, while WENO-RM(260) using ${\text {IS}}_i^5$-s has no oscillation.

In summary, we recommend to use ${\text {IS}}^r_i$-s for practical computation, because it is in a positive semi-definite quadratic form, and overcomes the potential loss of accuracy caused by negative values of ${\text {IS}}^r_i$ if a non-positive semi-definite quadratice form is used.