Skip to main content
SpringerLink
Log in

A Hybridized Discontinuous Galerkin Method for the Nonlinear Korteweg–de Vries Equation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

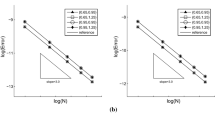
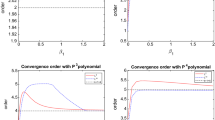
In this paper we introduce a hybridized discontinuous Galerkin (HDG) method for solving nonlinear Korteweg–de Vries type equations. Similar to a standard HDG implementation, we first express the approximate variables and numerical fluxes inside each element in terms of the approximate traces of the scalar variable (u), and its first derivative (\(u_x\)). These traces are assumed to be single-valued on each face. Next, we impose the conservation of numerical fluxes via two extra sets of equations. Using these global flux conservation conditions and applying the Newton–Raphson method, we construct a system of equations that can be solely expressed in terms of the increments of approximate traces in each iteration. Afterwards, we solve these equations, and substitute the approximate traces back into local equations over each element to obtain local approximate solutions. As for the time stepping scheme, we use the backward difference formulae. The method is proved to be stable for a proper choice of stabilization parameters. Through numerical examples, we observe that for a mesh with kth order elements, the computed u, p, and q show optimal convergence at order \(k+1\) in both linear and nonlinear cases, which improves upon previously employed techniques.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Alexanderian, A., Petra, N., Stadler, G., Ghattas, O.: A fast and scalable method for a-optimal design of experiments for infinite-dimensional bayesian nonlinear inverse problems, p. 29 (2014)

  2. Benzoni-Gavage, S., Danchin, R., Descombes, S., Jamet, D.: Structure of Korteweg models and stability of diffuse interfaces. Interfaces Free Bound. 7(4), 371–414 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  3. Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications, vol. 44. Springer, Berlin (2013)

    MATH  Google Scholar 

  4. Braginskii, S.I.: Transport processes in a plasma. Rev. Plasma Phys. 1, 205 (1965)

    Google Scholar 

  5. Buckingham, M.: Theory of acoustic attenuation, dispersion, and pulse propagation in unconsolidated granular materials including marine sediments. J. Acoust. Soc. Am. 102(5, 1), 2579–2596 (1997)

    Article  Google Scholar 

  6. Cockburn, B., Gopalakrishnan, J.: A characterization of hybridized mixed methods for second order elliptic problems. SIAM J. Numer. Anal. 42(1), 283–301 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  7. Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous galerkin, mixed, and continuous galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47(2), 1319–1365 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Gardner, C.L.: The quantum hydrodynamic model for semiconductor devices. SIAM J. Appl. Math. 54(2), 409–427 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  9. Heath, R.E., Gamba, I.M., Morrison, P.J., Michler, C.: A discontinuous Galerkin method for the Vlasov–Poisson system. J. Comput. Phys. 231(4), 1140–1174 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  10. Holmer, J.: The initial-boundary value problem for the Korteweg–de Vries equation. Commun. Partial Differ. Equ. 31(8), 1151–1190 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. Jain, A., Tamma, K.K.: Elliptic heat conduction specialized applications involving high gradients: local discontinuous galerkin finite element method—part 1. J. Therm. Stresses 33(4), 335–343 (2010)

    Article  Google Scholar 

  12. Kaladze, T., Aburjania, G., Kharshiladze, O., Horton, W., Kim, Y.: Theory of magnetized Rossby waves in the ionospheric E layer. J. Geophys. Res. Space Phys

  13. Kirby, R.M., Sherwin, S.J., Cockburn, B.: To CG or to HDG: a comparative study. J. Sci. Comput. 51(1), 183–212 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kloeckner, A., Warburton, T., Bridge, J., Hesthaven, J.S.: Nodal discontinuous Galerkin methods on graphics processors. J. Comput. Phys. 228(21), 7863–7882 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  15. Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. 39, 422–443 (1895)

    Article  MathSciNet  MATH  Google Scholar 

  16. Kostin, I., Marion, M., Texier-Picard, R., Volpert, V.: Modelling of miscible liquids with the Korteweg stress. ESAIM-Math. Modell. Numer. Anal. 37(5), 741–753 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  17. Kubatko, E.J., Westerink, J.J., Dawson, C.: hp discontinuous Galerkin methods for advection dominated problems in shallow water flow. Comput. Methods Appl. Mech. Eng. 196(1–3), 437–451 (2006)

    Article  MATH  Google Scholar 

  18. Larecki, W., Banach, Z.: Influence of nonlinearity of the phonon dispersion relation on wave velocities in the four-moment maximum entropy phonon hydrodynamics. Phys. D-Nonlinear Phenom. 266, 65–79 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Levy, D., Shu, C.-W., Yan, J.: Local discontinuous Galerkin methods for nonlinear dispersive equations. J. Comput. Phys. 196(2), 751–772 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  20. Loverich, J., Hakim, A., Shumlak, U.: A discontinuous Galerkin method for ideal two-fluid plasma equations. Commun. Comput. Phys. 9(2), 240–268 (2011)

    MathSciNet  MATH  Google Scholar 

  21. Michoski, C., Evans, J.A., Schmitz, P.G., Vasseur, A.: Quantum hydrodynamics with trajectories: the nonlinear conservation form mixed/discontinuous Galerkin method with applications in chemistry. J. Comput. Phys. 228(23), 8589–8608 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  22. Michoski, C., Meyerson, D., Isaac, T., Waelbroeck, F.: Discontinuous galerkin methods for plasma physics in the scrape-off layer of tokamaks. J. Comput. Phys. 274, 898–919 (2014)

    Article  MathSciNet  Google Scholar 

  23. Nguyen, N.C., Peraire, J., Cockburn, B.: An implicit high-order hybridizable discontinuous galerkin method for nonlinear convection–diffusion equations. J. Comput. Phys. 228(23), 8841–8855 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  24. Panda, N., Dawson, C., Zhang, Y., Kennedy, A.B., Westerink, J.J., Donahue, A.S.: Discontinuous Galerkin methods for solving Boussinesq–Green–Naghdi equations in resolving non-linear and dispersive surface water waves. J. Comput. Phys. 273, 572–588 (2014)

    Article  MathSciNet  Google Scholar 

  25. Peraire, J., Nguyen, N., Cockburn, B.: A hybridizable discontinuous Galerkin method for the compressible Euler and Navier–Stokes equations. AIAA Pap. 363, 2010 (2010)

    Google Scholar 

  26. Phillips, O.: Nonlinear dispersive waves. Annu. Rev. Fluid Mech. 6, 93–110 (1974)

    Article  MATH  Google Scholar 

  27. Shukla, P.K., Eliasson, B.: Colloquium: nonlinear collective interactions in quantum plasmas with degenerate electron fluids. Rev. Mod. Phys. 83(3), 885–906 (2011)

    Article  Google Scholar 

  28. Tassi, E., Morrison, P.J., Waelbroeck, F.L., Grasso, D.: Hamiltonian formulation and analysis of a collisionless fluid reconnection model. Plasma Phys. Control. Fusion 50(8), 085014 (2008)

  29. Woo, S.-B., Choi, Y.-K.: Development of finite volume model for KDV type equation. In: Zuo, Q.H., Dou, X.P., Ge, J.F., (Eds.), Asian and pacific coasts 2007, pp. 203–206, 2007. In: 4th International Conference on Asian and Pacific Coasts, Nanjing Hydraul Res Inst, Nanjing, Peoples Republic of China, Sept 21–24 (2007)

  30. Yagi, M., Horton, W.: Reduced Braginskii equations. Phys. Plasmas 1(7), 2135–2139 (1994)

    Article  Google Scholar 

  31. Yan, J., Shu, C.: A local discontinuous Galerkin method for KdV type equations. SIAM J. Numer. Anal. 40(2), 769–791 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  32. Yan, W., Liu, Z., Liang, Y.: Existence of solitary waves and periodic waves to a perturbed generalized KdV equation. Math. Model. Anal. 19(4), 537–555 (2014)

    Article  MathSciNet  Google Scholar 

  33. Zhang, Y., Kennedy, A.B., Panda, N., Dawson, C., Westerink, J.J.: Boussinesq–Green–Naghdi rotational water wave theory. Coast. Eng. 73, 13–27 (2013)

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to acknowledge the support of National Science Foundation Grant ACI 1339801. We also want to express our gratitude to the anonymous reviewers for their valuable comments to improve the quality of this paper.

Author information

Authors and Affiliations

  1. Computational Hydraulics Group (CHG), Institute for Computational Engineering and Sciences (ICES), The University of Texas at Austin, Austin, TX, 78712, USA

    Ali Samii, Craig Michoski & Clint Dawson

  2. Department of Aerospace Engineering and Engineering Mechanics, The University of Texas at Austin, Austin, TX, 78712, USA

    Ali Samii & Clint Dawson

  3. Department of Statistics, Colorado State University, Fort Collins, CO, 80523, USA

    Nishant Panda

Authors
  1. Ali Samii
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nishant Panda
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Craig Michoski
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Clint Dawson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ali Samii.

Additional information

The authors acknowledge the support of National Science Foundation Grant ACI 1339801.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Samii, A., Panda, N., Michoski, C. et al. A Hybridized Discontinuous Galerkin Method for the Nonlinear Korteweg–de Vries Equation. J Sci Comput 68, 191–212 (2016). https://doi.org/10.1007/s10915-015-0133-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-015-0133-1

Keywords

Mathematics Subject Classification

Search

Navigation