Abstract
We propose an exponential time-differencing method based on the leapfrog scheme for numerical integration of the generalized nonlinear Schrödinger-type equations. The key advantage of the proposed method over the widely used Fourier split-step method is that in the new method, numerical instability at high wavenumbers is strongly suppressed. This allows one to use time steps that considerably exceed the instability threshold, which leads to a proportional reduction of the computational time. Moreover, we introduce a technique that eliminates numerical instability at low-to-moderate wavenumbers that is common for methods based on the leapfrog scheme. We illustrate the performance of the proposed method with examples from two applications areas: deterministic wave turbulence and solitary waves.
















Similar content being viewed by others
Notes
at least three–four times in one spatial dimension and even more in higher dimensions .
Here “nearly” means that these quantities slightly fluctuate about, but do not systematically deviate from, their initial values.
There are no known “geometric integration” explicit methods of order higher than two, apart from fractional-step (also known as split-step) methods; see, e.g., [22]. Thus, one cannot increase the order of the ETD-LF (or the IF-LF) without making it implicit and thereby significantly slower, which would undo its main advantage over the SSM.
All conclusions of this paper remain valid also for
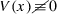 as long as \(\max |V(x)|\Delta t \ll 1\). Thus, for \(V(x)\sim x^2\), they may be altered, although the ETD- and IF-LF methods themselves will remain applicable for sufficiently small \({\Delta } t\).
as long as \(\max |V(x)|\Delta t \ll 1\). Thus, for \(V(x)\sim x^2\), they may be altered, although the ETD- and IF-LF methods themselves will remain applicable for sufficiently small \({\Delta } t\).The solution itself of the NLS cannot be used for this purpose. Indeed, since the system exhibits deterministic chaos, any two solutions that are initially different, no matter how slightly, will separate by an amount O(1) over the long times considered in this study.
of the benchmark solution.
We also carried out simulations of (44) with a potential term, V(x, y)u, and found the solution and its spectrum to be qualitatively similar to those obtained for \(V(x,y)\equiv 0\). We could not, however, perform the averaging of the results over the potential, as described in Sect. 5.2.1, because it would have been time prohibitive given our computational resources (two personal computers running Matlab).
In passing, let us note that the presence of nonvanishing correlations in space in time, as seen in panels (c) and (d), indicates that the solution has a hidden “plane-wave background” that oscillates in time as a whole. The presence of this background is also evident from the spectral peak at \(k_x=k_y=0\) in Fig. 13b.
Even though in both cases, the domains are tight in the sense defined in Sect. 5.1.2.
It was shown in [23] that fourth-order versions of the SSM have the same NI threshold as the second-order one.
Note that approximation (19) is not applicable for modes with those k where the spectrum varies by several orders of magnitude during its expansion; in particular, this occurs for \(|k|\gtrsim k_{\pi }\). For such modes, the size of the nonlinear term in (8) may be much greater than that of the terms on the l.h.s. when the spectrum expands.
References
Alonso-Mallo, I., Duran, A., Reguera, N.: Simulation of coherent structures in nonlinear Schrödinger-type equations. J. Comp. Phys. 229, 8180–8198 (2010)
Antoine, X., Bao, W., Besse, C.: Computational methods for the dynamics of the nonlinear Schrödinger/Gross-Pitaevskii equations. Comp. Phys. Comm. 184, 2621–2633 (2013)
Akhmediev, N., Dudley, J.M., Solli, D.R., Turitsyn, S.K.: Recent progress in investigating optical rogue waves. J. Opt. 15, 060201 (2013)
Onorato, M., Residori, S., Bortolozzo, U., Montinad, A., Arecchi, F.T.: Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 528, 47–89 (2013)
Zakharov, V.E., Dias, F., Pushkarev, A.: One-dimensional wave turbulence. Phys. Rep. 398, 1–65 (2004)
Korotkevich, A.O.: Influence of the condensate and inverse cascade on the direct cascade in wave turbulence. Math. Comp. Simul. 82, 1228–1238 (2012)
Weideman, J.A.C., Herbst, B.M.: Split-step methods for the solution of the nonlinear Schrödinger equation. SIAM J. Numer. Anal. 23, 485–507 (1986)
Chan, T.F., Kerkhoven, T.: Fourier methods with extended stability intervals for the Korteweg-de Vries equation. SIAM J. Numer. Anal. 22, 441–454 (1985)
Lakoba, T.I.: Instability of the finite-difference split-step method applied to the nonlinear Schrödinger equation. I. standing soliton. Num. Meth. Part. Diff. Eqs 32, 1002–1023 (2016)
Kremp, T., Freude, W.: Fast split-step wavelet collocation method for WDM system parameter optimization. J. Lightwave Technol. 23, 1491–1502 (2005)
Lakoba, T.I.: Instability of the split-step method for a signal with nonzero central frequency. J. Opt. Soc. Am. B 30, 3260–3271 (2013)
Certaine, J.: The solution of ordinary differential equations with large time constants, in: A. Ralston, H.S. Wilf. (Eds.), Mathematical methods for digital computers, Wiley, New York, 1960, pp. 128–132
Pope, D.A.: An exponential method of numerical integration of ordinary differential equations. Commun. ACM 6, 491–493 (1963)
Lawson, J.D.: Generalized Runge-Kutta processes for stable systems with large Lipschitz constants. SIAM J. Numer. Anal. 4, 372–380 (1967)
Milewski, P.A., Tabak, E.: A pseudospectral procedure for the solution of nonlinear wave equations with examples from free-surface flow. SIAM J. Sci. Comp. 21, 1102–1114 (1999)
Cox, S.M., Matthews, P.C.: Exponential time differencing for stiff systems. J. Comp. Phys. 176, 430–455 (2002)
Fei, Z., Perez-Garcia, V.M., Vazquez, L.: Numerical simulation of nonlinear Schrödinger systems: a new conservative scheme. Appl. Math. Comp. 71, 165–177 (1995)
Zhang, Y., Bao, W.: Dynamics of the center of mass in rotating Bose-Einstein condensates. Appl. Numer. Math. 57, 697–709 (2007)
Fornberg, B., Whitham, G.B.: A numerical and theoretical study of certain nonlinear wave phenomena. Phil. Trans. Roy. Soc. 289, 373–404 (1978)
Hairer, E., Lubich, C., Wanner, G.: Geometric numerical integration illustrated by the Störmer-Verlet method. Acta Numer. 12, 399–450 (2003)
Islas, A.L., Karpeev, D.A., Schober, C.M.: Geometric integrators for the nonlinear Schrödinger equation. J. Comp. Phys. 173, 116–148 (2001)
Yoshida, H.: Construction of higher order symplectic integrators. Phys. Lett. A 150, 262–268 (1990)
Lakoba, T.I.: Instability analysis of the split-step Fourier method on the background of a soliton of the nonlinear Schrödinger equation. Num. Meth. Part. Diff. Eqs. 28, 641–669 (2012)
Zhao, S., Ovadia, J., Liu, X., Zhang, Y.-T., Nie, Q.: Operator splitting integration factor methods for stiff reaction-diffusion-advection systems. J. Comput. Phys. 230, 5996–6009 (2011)
Jiang, T., Zhang, Y.-T.: Krylov implicit integration factor WENO methods for semilinear and fully nonlinear advection-diffusion-reaction equations. J. Comput. Phys. 253, 368–388 (2013)
Suhov, A.Y.: An accurate polynomial approximation of exponential integrators. J. Sci. Comput. 60, 684–698 (2014)
Jung, C.-Y., Nguyen, T.B.: Semi-analytical time differencing methods for stiff problems. J. Sci. Comput. 63, 355–373 (2015)
Ju, L., Zhang, J., Zhu, L., Du, Q.: Fast explicit integration factor methods for semilinear parabolic equations. J. Sci. Comput. 62, 431–455 (2015)
Zhu, L., Ju, L., Zhao, W.: Fast high-order compact exponential time differencing Runge-Kutta methods for second-order semilinear parabolic equations. J. Sci. Comput. 67, 1043–1065 (2016)
Lu, D., Zhang, Y.-T.: Krylov integration factor method on sparse grids for high spatial dimension convection-diffusion equations. J. Sci. Comput. 69, 736–763 (2016)
Agrawal, G.P.: Nonlinear fiber optics, 3rd Ed., Academic Press, San Diego, (2001), Sec. 5.1
Dahlby, M., Owren, B.: Plane wave stability of some conservative schemes for the cubic Schrödinger equation. ESAIM: M2AN 43, 677–687 (2009)
Briggs, W.L., Newell, A.C., Sarie, T.: Focusing: a mechanism for instability of nonlinear finite difference equations. J. Comp. Phys. 51, 83–106 (1983)
Zakharov, V.E., Shabat, A.B.: Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34, 62–69 (1972)
Lakoba, T.I.: Effect of noise on extreme events probability in a one-dimensional nonlinear Schrödinger equation. Phys. Lett. A 379, 1821–1827 (2015)
Lushnikov, P.M., Vladimirova, N.: Non-Gaussian statistics of multiple filamentation. Opt. Lett. 35, 1965–1967 (2010)
Dutykh, D., Pelinovsky, E.: Numerical simulation of a solitonic gas in KdV and KdV-BBM equations. Phys. Lett. A 378, 3102–3110 (2014)
Acknowledgements
This work was supported in part by the NSF Grant DMS-1217006. I thank the anonymous referees whose constructive comments helped improve this paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Comparison of High-k NI of IF-LF and SSM
We will first illustrate that the high-k NI of these two methods is the same as long as the spectrum of the background solution has negligible content in the vicinity of the resonant wavenumbers \(k_{\pi m}\), defined in (18). Then we will present a heuristic argument why the NI of the IF-LF appears to be stronger than that of the SSM when the solution’s spectrum expands to and beyond \(k_{\pi m}\).
Figure 17 shows a typical spectrum of a soliton initial condition,
whose evolution is computed by the IF-LF (Fig. 17a) or ETD-LF (Fig. 17b) with a time step exceeding the NI threshold. The spectrum computed by the SSM is indistinguishable from that computed by the IF-LF. The white noise \(\xi (x)\) of magnitude of order \(10^{-10}\) is added in (47) to facilitate controllable observation of NI; in all simulations \(\xi (x)\) was the same. The two spikes in the vicinity of \(k_{\pi }\) in Fig. 17a are the unstable modes. In Table 2 we list the locations and magnitudes of these spikes for the SSM as one varies \(\Delta t\). The corresponding locations for the IF-LF were found to be exactly the same as for the SSM, while the magnitudes were within \(\pm 5\)%. This demonstrates the close similarity between the high-k NIs of the two methods.
Spectra of the numerical solution of (1) with \(\gamma =2\), \(V(x)\equiv 0\), and the near-soliton initial condition (47). The domain length \(L=128\pi \) and the number of grid points \(N=2^{12}\) are as in the experiment reported in [23]. Panel a shows a typical spectrum obtained at \(t=1000\) with the IF-LF with \(\Delta t_\mathrm{thresh}< \Delta t< 2\Delta t_\mathrm{thresh}\). (For some \(\Delta t\), there may be more than two unstable modes around \(k_{\pi }\); see Table 2.) Panel b shows the spectrum obtained by the ETD-LF at \(t=10,000\) (i.e. 10 times longer than in a) with \(\Delta t=0.05\). Stabilization, discussed in Sect. 4, did not need to be applied for either the IF- or ETD-LF
Figure 17b shows that the NI remains suppressed in the solution obtained by the ETD-LF over a very long time even when \(\Delta t\) exceeds the threshold more than 15-fold. Note that unlike in Fig. 17a, here the spikes do not correspond to numerically unstable modes. These spikes occur in the first few time units of the evolution (probably due to a discretization error) and then remain almost unchanged over a very long time.
We will now present a heuristic explanation of why the unstable modes in the IF-LF method appear to grow much faster than in the SSM (see Fig. 1a). In Fig. 18 we provide evidence that this “extra” growth is not exponential. Rather, it occurs only when the spectrum expands so much that near \(\pm k_{\pi m}\) it considerably exceeds the noise floor. Figure 18 shows that the magnitude of unstable modes near \(k_{\pi }\) has increased by almost two orders of magnitude precisely at those short time intervals of duration \(\sim 0.1\) when the solution’s spectrum has expanded beyond \(k_{\pi }\). After the spectrum has shrunk (Fig. 18c), these modes retain their abnormally increased amplitude. They proceed on growing slowlyFootnote 12 until the next instance of spectrum expansion beyond \(k_{\pi }\) occurs.
Spectra (on the \(\log _{10}\)-scale) of the solution of the pure NLS obtained by the IF-LF with \(\Delta t=3.2\cdot 10^{-4} > \Delta t_\mathrm{thresh}\). Parameters are similar to those in Sect. 5.1, but \(L=80\pi \), \(N=2^{13}\). Shown are successive stages of the spectrum expansion beyond \(k_{\pi }\) (a, b) and subsequent shrinking (c)
In contrast, the SSM does not produce such quickly growing modes; numerically unstable modes in its solution grow at an approximately constant rate and independently of the behavior of the spectrum. This indicates that a possible reason for the quickly growing modes in the IF-LF is the presence of two solutions of its three-level difference equation (8).Footnote 13 Indeed, the SSM, being a two-level method, has only one solution of its difference scheme. An indirect confirmation of our conjecture comes from the solution by the ETD-LF, which, like the IF-LF, is a three-level method but, unlike the IF-LF, has no or a greatly reduced high-k NI. Figure 1 shows that the ETD-LF solution also develops spectral peaks around \(|k|=k_{\pi m}\), and these peaks grow only when the spectrum expands beyond their locations. However, we have been unable to quantitatively explain the formation of these peaks around \(|k|=k_{\pi m}\) during spectrum expansions.
Appendix B: Reduction of Spectral Distortions Near \(|k|=k_{\pi }\) and \(k_{2\pi }\)
We have observed that the distortions in questions appeared only near \(k_{\pi m}\) but not, for example, near \(k_{\pi /2}\) (where \(k_{\pi /2}^2\Delta t=\pi /2\)). Therefore, one expects that distortions for \(|k|\approx k_{\pi }\) will be reduced if one somehow could use a twice as small time step, \(\Delta t_\mathrm{new}=\Delta t/2\), to resolve the dynamics of those specific Fourier modes (because then \(k_{\pi }^2\Delta t_\mathrm{new}=\pi /2\)). This can be done by using, instead of (8), a formula
where the term on the r.h.s. is found by the standard linear extrapolation:
For the result shown in Fig. 1(b) with the green solid line, this technique was applied to harmonics with \(|k|\in [k_{\pi }-12,\,k_{\pi }+10]\) (for reference, \(k_{\pi }=41.8\) there).
We have empirically found that this idea does not work if extended to \(|k|\approx k_{2\pi }\), where one would use \(\Delta t_\mathrm{new}=\Delta t/4\). The problem appeared to be in a linear NI that sets in when the term \(\widehat{\mathcal N}(t_{n+3/4})\), required for an extension of (48a), was computed by an extrapolation analogous to (48b).
Therefore we used a different idea for \(|k|\approx k_{2\pi }\). Those harmonics do not need to be resolved accurately, because they contribute little to the solution. Rather, one simply needs to arrest their abnormal growth (see the spectrum with “no corrections” in Fig. 1b). A well-known way to gain stability at the expense of accuracy is to use a linearly implicit method:
where \(\widehat{\mathcal N}(t_{n+1/2})\) is computed by (48b). We have empirically found that the best results are obtained when (49) is applied every third step. The solid green line in Fig. 1b shows the result of doing so for harmonics with \(|k|\in (k_{\pi }+10,\,k_{2\pi }+9]\).
Rights and permissions
About this article
Cite this article
Lakoba, T.I. Long-Time Simulations of Nonlinear Schrödinger-Type Equations using Step Size Exceeding Threshold of Numerical Instability. J Sci Comput 72, 14–48 (2017). https://doi.org/10.1007/s10915-016-0346-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0346-y



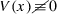 as long as
as long as 
