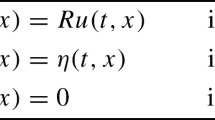Computation of Time Optimal Control Problems Governed by Linear Ordinary Differential Equations

Abstract

In this paper, a novel numerical algorithm is presented to compute the optimal time of a time optimal control problem where the governing system is a linear ordinary differential equation. By the equivalence between time optimal control problem and norm optimal control problem, computation of the optimal time can be obtained by solving a sequence of norm optimal control problems, which are transferred into their Lagrangian dual problems. The nonsmooth structure of the dual problem is approximated by the iteratively reweighted least square strategy. Several numerical tests are given to show the efficiency of the proposed algorithm.

Appendix

Proof of Lemma 1

The proof is divided into four steps as follows.

Step 1.

$$\begin{aligned} \text{ If } \mu \ne 0,\; \text{ then } B^\mathrm {T}\varphi (t;T,\mu )= 0 \text { at most finite }t\in [0,T]. \end{aligned}$$

(27)

It can be proved by contradiction. Assume that $B^\mathrm {T}\varphi (t;T,\mu )= 0$ at infinite $t\in [0,T]$. Since $B^\mathrm {T}\varphi (t;T,\mu )$ is analytic, we then obtain $B^\mathrm {T}\varphi (t;T,\mu )\equiv 0$ in [0, T], which implies that

$$\begin{aligned} B^\mathrm {T}\mu =0,\, B^\mathrm {T}A^\mathrm {T}\mu =0,\ldots , B^\mathrm {T}(A^\mathrm {T})^{n-1}\mu =0. \end{aligned}$$

(28)

From $(H_2)$ and (28), it follows that

$$\begin{aligned} \mu =0, \end{aligned}$$

which leads to a contradiction.

Step 2. The bang-bang property of $(TP)^M$.

By Pontryagin’s maximum principle (see Theorem 3.5 in Chapter 3 of [24]), there exists $\xi \in {\mathbb {R}}^n$ with $\Vert \xi \Vert =1$ such that

$$\begin{aligned} \max _{\Vert v\Vert \le M}\langle \varphi (t;t^*(M),\xi ),Bv\rangle =\langle \varphi (t;t^*(M),\xi ),Bu_M^*(t)\rangle , \text { for a.e.}\;t\in (0,t^*(M)). \end{aligned}$$

This, together with (27), indicates the bang-bang property of $(TP)^M$. Then the uniqueness of the optimal control follows.

Step 3. For any $\tau \in (0,T)$, there exists a generic positive constant $C(\tau )$ dependent on $\tau$, such that

$$\begin{aligned} \Vert \varphi (0;\tau ,\mu )\Vert \le C(\tau )\int _0^\tau \Vert B^{\mathrm {T}}\varphi (t;\tau ,\mu )\Vert \,dt, \quad \forall \,\mu \in {\mathbb {R}}^n. \end{aligned}$$

(29)

It can be proved by contradiction. Assume that there exists $\mu _\ell \in {\mathbb {R}}^n$ with $\Vert \mu _\ell \Vert =1$ and

$$\begin{aligned} \frac{\displaystyle \int _0^\tau \Vert B^\mathrm {T}\varphi (t;\tau ,\mu _\ell )\Vert \,dt}{\Vert \varphi (0;\tau ,\mu _\ell )\Vert }< \frac{1}{\ell },\quad \forall \,\ell \ge 1. \end{aligned}$$

(30)

Since $\Vert \mu _\ell \Vert =1$, there exists a subsequence of $\{\mu _\ell \}_{\ell \ge 1}$, still denoted by $\{\mu _\ell \}$, and $\mu _0\in {\mathbb {R}}^n$, such that

$$\begin{aligned} \lim _{\ell \rightarrow \infty }\mu _\ell =\mu _0\text { and }\Vert \mu _0\Vert =1. \end{aligned}$$

Passing to the limit for $\ell \rightarrow +\infty$ in (30), we have that

$$\begin{aligned} \frac{\displaystyle \int _0^\tau \Vert B^\mathrm {T}\varphi (t;\tau ,\mu _0)\Vert \,dt}{\Vert \varphi (0;\tau ,\mu _0)\Vert }=0. \end{aligned}$$

This implies that $B^\mathrm {T}\varphi (t;\tau ,\mu _0)=0$ for a.e. $\; t\in [0,T]$ and contradicts (27).

Step 4. By (29) and the equivalence between the observability and controllability, see e.g. Theorem 2.1 in [19], we get that for any $z_0\in {\mathbb {R}}^n$, there exists a control $u\in L^\infty (0,\tau ;{\mathbb {R}}^m)$ with

$$\begin{aligned} \Vert u\Vert _{L^\infty (0,\tau ;{\mathbb {R}}^m)}\le C(\tau )\Vert z_0\Vert , \end{aligned}$$

(31)

such that the solution $z(\cdot )$ to the equation

$$\begin{aligned} {\left\{ \begin{array}{ll} z'(t)+Az(t)=Bu(t),&{}t\in (0,\tau ),\\ z(0)=z_0 \end{array}\right. } \end{aligned}$$

satisfies that $z(\tau )=0$.

By (31) and using the same argument as in [22], we have that (ii), (iii) and (iv) hold. Finally, the bang-bang property and the uniqueness of the optimal control for $(NP)^T$ follow from (iv) and Step 2. $\square$

Proof of Proposition 1

By changing variables, it suffices to show that there exists a solution $(T,y(\cdot ),u(\cdot ),\psi (\cdot ))$ to the the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle y'(t)+ Ay(t)= Bu(t), &{} t\in (0,T),\\ \displaystyle \psi '(t)= A^\mathrm {T}\psi (t),&{}t\in (0,T),\\ \displaystyle u(t)=M\frac{B^\mathrm {T}\psi (t)}{\Vert B^\mathrm {T}\psi (t)\Vert },&{}t\in (0,T),\\ \displaystyle M=\int _0^T\Vert B^\mathrm {T}\psi (t)\Vert \,dt,\\ \displaystyle y(0)=y_0,\\ \displaystyle y(T)=0,\\ \end{array}\right. } \end{aligned}$$

(32)

where T is the optimal time to $(TP)^M$ and $u(\cdot )$, when extended by zero to $(T, +\infty )$, is the optimal control to $(TP)^M$.

On one hand, let $y^*(\cdot )$ and $u^*(\cdot )$ be the optimal state and optimal control to $(TP)^M$, respectively and let $\mu ^*$ be a minimizer of $J^{t^*(M)}(\cdot )$. By (iv) in Lemma 1 and (iii) in Lemma 2, we have that

$$\begin{aligned} \left( t^*(M),y^*(\cdot ), u^*(\cdot ),\varphi (\cdot ;t^*(M),\mu ^*)\right) \end{aligned}$$

is a solution to (32). On the other hand, for any solution $( T, y(\cdot ), u(\cdot ), \psi (\cdot ))$ to (32) and any $\nu \in {\mathbb {R}}^n$, multiplying the first equation of (32) by $\varphi (\cdot ;T,\nu )$ and integrating it over (0, T), we get that

$$\begin{aligned} \int _0^T\Vert B^\mathrm {T}\psi (t)\Vert \,dt\int _0^T\frac{\langle B^\mathrm {T}\psi (t),B^\mathrm {T}\varphi (t;T,\nu ) \rangle }{\Vert B^\mathrm {T}\psi (t)\Vert }\,dt +\langle \varphi (0;T,\nu ),y_0\rangle =0. \end{aligned}$$

This, together with (ii) in Lemma 2, indicates that

$$\begin{aligned} \psi (T)\text { is a minimizer of } J^T(\cdot ). \end{aligned}$$

(33)

It follows from the third equality, the fourth equality in (32), (33) and (iii) in Lemma 2 that

$$\begin{aligned} u(\cdot ),\text { when extended by zero to }(T,+\infty ), \text { is the optimal control to }(NP)^T. \end{aligned}$$

(34)

By the third equality in (32) and (34), we obtain that $M=M^*(T)$, which, combined with (iii) and (iv) in Lemma 1, implies

$$\begin{aligned} T=t^*(M). \end{aligned}$$

(35)

From this equation, (34) and (iv) in Lemma 1, we obtain the conclusion. $\square$

Proof of Lemma 2

(i) It is obvious that $J_\varepsilon ^T(\cdot )$ is continuous and convex. By (29), we have that

$$\begin{aligned} J_\varepsilon ^T(\mu )\ge & {} \frac{1}{2}\left( \int _0^T\Vert B^\mathrm {T}\varphi (s;T,\mu )\Vert \,ds\right) ^2 -C(T)\Vert y_0\Vert \int _0^T\Vert B^\mathrm {T}\varphi (s;T,\mu )\Vert \,ds+\varepsilon \Vert \mu \Vert \\= & {} \frac{1}{2}\left( \int _0^T\Vert B^\mathrm {T}\varphi (s;T,\mu )\Vert \,ds-C(T)\Vert y_0\Vert \right) ^2 -\frac{1}{2}C(T)^2\Vert y_0\Vert ^2+\varepsilon \Vert \mu \Vert . \end{aligned}$$

We will prove

$$\begin{aligned} \lim _{\Vert \mu \Vert \rightarrow +\infty }\int _0^T\Vert B^\mathrm {T}\varphi (s;T,\mu )\Vert \,ds=+\infty \end{aligned}$$

(36)

by contradiction, and the coercivity follows immediately. Assume that there exist $\{\mu _k\}\subset {\mathbb {R}}^n$ and a positive constant C which is independent of k, such that $\Vert \mu _k\Vert \rightarrow +\infty$ and

$$\begin{aligned} \int _0^T\Vert B^\mathrm {T}\varphi (s;T,\mu _k)\Vert \,ds\le C \text { for each }k\ge 1. \end{aligned}$$

(37)

Let $\displaystyle v_k\triangleq \frac{\mu _k}{\Vert \mu _k\Vert }$, then there exists a subsequence of $\{v_k\}_{k\ge 1}$, still denoted by the same way, and $v_0\in {\mathbb {R}}^n$ with $\Vert v_0\Vert =1$ and $v_k\rightarrow v_0$. From (37), it follows that

$$\begin{aligned} \int _0^T\Vert B^\mathrm {T}\varphi (s;T,v_k)\Vert \,ds\le \frac{C}{\Vert \mu _k\Vert }\text { for each }k\ge 1. \end{aligned}$$

Passing to the limit for $k\rightarrow \infty$ in the above inequality, we get that

$$\begin{aligned} \displaystyle \int _0^T\Vert B^\mathrm {T}\varphi (s;T,v_0)\Vert \,ds=0. \end{aligned}$$

This implies that $v_0=0$, which leads to a contradiction. By the continuity and the coercivity of $J_\varepsilon ^T(\cdot )$, there exists a minimizer $\mu _\varepsilon ^*$.

Next we prove that $\mu _\varepsilon ^*\ne 0$. If not, we have that for any $\mu \in {\mathbb {R}}^n$,

$$\begin{aligned} J_\varepsilon ^T(\lambda \mu )=\frac{\lambda ^2}{2} \left( \int _0^T\Vert B^\mathrm {T}\varphi (s;T,\mu )\Vert \,ds\right) ^2+\lambda \langle y_0,\varphi (0;T,\mu )\rangle +\lambda \varepsilon \Vert \mu \Vert \ge 0,\quad \forall \, \lambda >0. \end{aligned}$$

and

$$\begin{aligned} J_\varepsilon ^T(-\lambda \mu )=\frac{\lambda ^2}{2} \left( \int _0^T\Vert B^\mathrm {T}\varphi (s;T,\mu )\Vert \,ds\right) ^2-\lambda \langle y_0,\varphi (0;T,\mu )\rangle +\lambda \varepsilon \Vert \mu \Vert \ge 0,\quad \forall \, \lambda >0. \end{aligned}$$

From the above two inequalities, we obtain that

$$\begin{aligned} |\langle y_0,\varphi (0;T,\mu )\rangle |\le \frac{\lambda }{2} \left( \int _0^T\Vert B^\mathrm {T}\varphi (s;T,\mu )\Vert \,ds\right) ^2+\varepsilon \Vert \mu \Vert ,\quad \forall \, \lambda >0. \end{aligned}$$

Letting $\lambda \rightarrow 0^+$, we obtain that

$$\begin{aligned} |\langle y_0,\varphi (0;T,\mu )\rangle |\le \varepsilon \Vert \mu \Vert ,\quad \forall \,\mu \in {\mathbb {R}}^n, \end{aligned}$$

i.e.,

$$\begin{aligned} |\langle e^{-AT}y_0,\mu \rangle |\le \varepsilon \Vert \mu \Vert , \quad \forall \,\mu \in {\mathbb {R}}^n. \end{aligned}$$

This implies $\Vert e^{-AT}y_0\Vert \le \varepsilon$, which contradicts $T<T_\varepsilon ^*$.

(ii) On one hand, if $\mu _\varepsilon ^*$ is a minimizer of $J_\varepsilon ^T(\cdot )$, we have that

$$\begin{aligned} \frac{J_\varepsilon ^T(\mu _\varepsilon ^*+\lambda \nu )-J_\varepsilon ^T(\mu _\varepsilon ^*)}{\lambda } \ge 0, \quad \forall \,\lambda >0,\quad \forall \, \nu \in {\mathbb {R}}^n. \end{aligned}$$

Letting $\lambda \rightarrow 0^+$ in the above inequality, one can check that (5) holds. On the other hand, since $J_\varepsilon ^T(\cdot )$ is convex and the minimizer is nonzero, then $\nabla J_\varepsilon ^T(\mu _\varepsilon ^*) =0$ (which is equation (5)) implies $\mu _\varepsilon ^*\ne 0$ is a minimizer of $J_\varepsilon ^T(\cdot )$.

(iii) Let $\mu _\varepsilon ^*$ be a minimizer of $J_\varepsilon ^T(\cdot )$ and $u_\varepsilon ^*$ be defined by (6). First, we can prove that $u_\varepsilon ^*$ is an admissible control for $(NP)_\varepsilon ^T$. Let $y(\cdot )$ be the solution to

$$\begin{aligned} \left\{ \begin{array}{l} y'(t)+Ay(t)=Bu_\varepsilon ^*(t),\,t\in ( 0,T),\\ y(0)=y_0. \end{array}\right. \end{aligned}$$

Multiplying the first equation of the above system by $\varphi (\cdot ;T,\nu )$ and integrating it over (0, T), we get that

$$\begin{aligned} \langle \nu ,y(T)\rangle -\langle \varphi (0;T,\nu ),y_0\rangle =\int _0^T\langle u_\varepsilon ^*(t), B^\mathrm {T}\varphi (t;T,\nu )\rangle \,dt. \end{aligned}$$

From the latter and (6) it follows that

$$\begin{aligned}&\langle \nu ,y(T)\rangle \\&\quad = \langle \varphi (0;T,\nu ),y_0\rangle +\int _0^T\langle u_\varepsilon ^*(t), B^\mathrm {T}\varphi (t;T,\nu )\rangle \,dt\\&\quad =\langle \varphi (0;T,\nu ),y_0\rangle +\int _0^T\Vert B^\mathrm {T}\varphi (t;T,\mu _\varepsilon ^*)\Vert \,dt\int _0^T\frac{\langle B^\mathrm {T}\varphi (t;T,\mu _\varepsilon ^*), B^\mathrm {T}\varphi (t;T,\nu ) \rangle }{\Vert B^\mathrm {T}\varphi (t;T,\mu _\varepsilon ^*)\Vert }\,dt, \end{aligned}$$

which, combined with (5), indicates that

$$\begin{aligned} |\langle \nu ,y(T)\rangle |=\left| \varepsilon \frac{\langle \mu _\varepsilon ^*, \nu \rangle }{\Vert \mu _\varepsilon ^*\Vert }\right| \le \varepsilon \Vert \nu \Vert , \quad \forall \, \nu \in {\mathbb {R}}^n. \end{aligned}$$

This implies $\Vert y(T)\Vert \le \varepsilon$ and $u_\varepsilon ^*$ is an admissible control for $(NP)_\varepsilon ^T$.

Then, we prove that $u_\varepsilon ^*$ is an optimal control for $(NP)_\varepsilon ^T$. For any $u\in L^\infty (0,+\infty ;{\mathbb {R}}^m)$ satisfying that

$$\begin{aligned} \left\{ \begin{array}{l} h'(t)+Ah(t)=Bu(t),\,t\in ( 0,T),\\ h(0)=y_0,\\ \Vert h(T)\Vert \le \varepsilon , \end{array}\right. \end{aligned}$$

multiplying the first equation of the above system by $\varphi (\cdot ;T,\mu _\varepsilon ^*)$ and integrating it over (0, T), we get that

$$\begin{aligned} \langle \mu _\varepsilon ^*, h(T)\rangle -\langle \varphi (0;T,\mu _\varepsilon ^*),y_0\rangle =\int _0^T \langle u(t), B^{\mathrm {T}}\varphi (t;T,\mu _\varepsilon ^*)\rangle \,dt. \end{aligned}$$

This, together with (5), implies that

$$\begin{aligned} \langle \mu _\varepsilon ^*, h(T)\rangle -\int _0^T \langle u(t), B^{\mathrm {T}}\varphi (t;T,\mu _\varepsilon ^*)\rangle \,dt =-\varepsilon \Vert \mu _\varepsilon ^*\Vert -\left( \int _0^T\Vert B^\mathrm {T}\varphi (t;T,\mu _\varepsilon ^*)\Vert \,dt\right) ^2. \end{aligned}$$

Since $\Vert h(T)\Vert \le \varepsilon$, it follows from the latter equality that

$$\begin{aligned} \int _0^T \langle u(t), B^{\mathrm {T}}\varphi (t;T,\mu _\varepsilon ^*)\rangle \,dt -\left( \int _0^T\Vert B^\mathrm {T}\varphi (t;T,\mu _\varepsilon ^*)\Vert \,dt\right) ^2 =\langle \mu _\varepsilon ^*, h(T)\rangle +\varepsilon \Vert \mu _\varepsilon ^*\Vert \ge 0. \end{aligned}$$

Thus

$$\begin{aligned} \Vert u\Vert _{L^\infty (0,T;{\mathbb {R}}^m)}\ge \int _0^T\Vert B^\mathrm {T}\varphi (t;T,\mu _\varepsilon ^*)\Vert \,dt= \Vert u_\varepsilon ^*\Vert _{L^\infty (0,T;{\mathbb {R}}^m)}. \end{aligned}$$

This shows that $u_\varepsilon ^*$ is an optimal control to $(NP)_\varepsilon ^T$ and

$$\begin{aligned} M_\varepsilon ^*(T)=\displaystyle \int _0^T\Vert B^\mathrm {T}\varphi (t;T,\mu _\varepsilon ^*)\Vert \,dt. \end{aligned}$$

$\square$

Proof of Proposition 2

Let $0<\varepsilon <\Vert y_0\Vert$ and $0<T<T_\varepsilon ^*$. For any $\mu _1,\,\mu _2\in {\mathbb {R}}^n$, $0<\alpha <1$, we have that

$$\begin{aligned}&J_\varepsilon ^T(\alpha \mu _1+(1-\alpha )\mu _2)\nonumber \\&\quad = \frac{1}{2}\left( \int _0^T\Vert B^\mathrm {T}\varphi (s;T,\alpha \mu _1+(1-\alpha )\mu _2)\Vert \,ds\right) ^2\nonumber \\&\qquad +\,\langle y_0,\varphi (0;T,\alpha \mu _1+(1-\alpha )\mu _2)\rangle +\varepsilon \Vert \alpha \mu _1+(1-\alpha )\mu _2\Vert \nonumber \\&\quad \le \frac{1}{2}\left( \int _0^T(\alpha \Vert B^\mathrm {T}\varphi (s;T, \mu _1)\Vert +(1-\alpha )\Vert B^\mathrm {T}\varphi (s;T, \mu _2)\Vert )\,ds\right) ^2\nonumber \\&\qquad +\,\alpha \langle y_0,\varphi (0;T, \mu _1)\rangle +(1-\alpha )\langle y_0,\varphi (0;T, \mu _2)\rangle +\alpha \varepsilon \Vert \mu _1\Vert +(1-\alpha )\varepsilon \Vert \mu _2\Vert \nonumber \\&\quad \le \frac{\alpha }{2}\left( \int _0^T\Vert B^\mathrm {T}\varphi (s;T, \mu _1)\Vert \,ds\right) ^2+\frac{1-\alpha }{2}\left( \int _0^T\Vert B^\mathrm {T}\varphi (s;T, \mu _2)\Vert \,ds\right) ^2\nonumber \\&\qquad +\,\alpha \langle y_0,\varphi (0;T, \mu _1)\rangle +(1-\alpha )\langle y_0,\varphi (0;T, \mu _2)\rangle +\alpha \varepsilon \Vert \mu _1\Vert +(1-\alpha )\varepsilon \Vert \mu _2\Vert \nonumber \\&\quad =\alpha J_\varepsilon ^T( \mu _1)+(1-\alpha )J_\varepsilon ^T( \mu _2). \end{aligned}$$

(38)

First, we notice that the first inequality in (38) becomes equality if and only if there exists a constant $k\ge 0$ and a function $\beta (\cdot ):\,[0,T]\rightarrow [0,+\infty )$, such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _1=k\mu _2,\\ B^\mathrm {T}\varphi (t;T,\mu _1)=\beta (t)B^\mathrm {T}\varphi (t;T,\mu _2), \text { for a.e. }t\in (0,T). \end{array}\right. } \end{aligned}$$

These imply that the first inequality in (38) becomes equality if and only if there exists a constant $k\ge 0$, such that

$$\begin{aligned} \mu _1=k\mu _2. \end{aligned}$$

Then, the second inequality in (38) becomes equality if and only if

$$\begin{aligned} \int _0^T\Vert B^\mathrm {T}\varphi (t;T,\mu _1)\Vert \,dt=\int _0^T\Vert B^\mathrm {T}\varphi (t;T,\mu _2)\Vert \,dt. \end{aligned}$$

Hence $J_\varepsilon ^T(\alpha \mu _1+(1-\alpha )\mu _2)=\alpha J_\varepsilon ^T( \mu _1)+(1-\alpha )J_\varepsilon ^T( \mu _2)$ if and only if $\mu _1=\mu _2$. This shows that $J_\varepsilon ^T(\cdot )$ is strictly convex and it has a unique minimizer. $\square$