Laguerre Functions and Their Applications to Tempered Fractional Differential Equations on Infinite Intervals

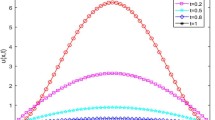
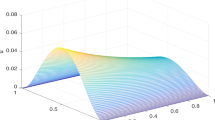
Abstract

Tempered fractional diffusion equations (TFDEs) involving tempered fractional derivatives on the whole space were first introduced in Sabzikar et al. (J Comput Phys 293:14–28, 2015), but only the finite-difference approximation to a truncated problem on a finite interval was proposed therein. In this paper, we rigorously show the well-posedness of the models in Sabzikar et al. (2015), and tackle them directly in infinite domains by using generalized Laguerre functions (GLFs) as basis functions. We define a family of GLFs and derive some useful formulas of tempered fractional integrals/derivatives. Moreover, we establish the related GLF-approximation results. In addition, we provide ample numerical evidences to demonstrate the efficiency and “tempered” effect of the underlying solutions of TFDEs.

Appendices

Appendix A: Proof of Lemma 2.2

We first prove (2.42)–(2.43). Recall the fractional integral formula of hypergeometric functions see [2, P. 287]: for real $b,\mu \ge 0,$

$$\begin{aligned} x^{b+\mu -1}\,{}_1F_1(a;b+\mu ; x)=\frac{\Gamma (b+\mu )}{\Gamma (b)\Gamma (\mu )}\int _0^x (x-t)^{\mu -1}t^{b-1} {}_1F_1(a;b; t)\, \mathrm{d}t,\quad x\in {\mathbb {R}}^+. \end{aligned}$$

(A.1)

Taking $a=-n,~b=\alpha +1$ and using the hypergeometric representation (2.34) of the Laguerre polynomials, we obtain

$$\begin{aligned} x^{\alpha +\mu } L_n^{(\alpha +\mu )}(x) =\frac{\Gamma (n+\alpha +\mu +1)}{\Gamma (n+\alpha +1)\Gamma (\mu )}\int _{0}^x {(x-t)^{\mu -1}} t^\alpha L_n^{(\alpha )}(t)\, \mathrm{d}t, \end{aligned}$$

which yields (2.42), i.e.,

$$\begin{aligned} {}_{0}\mathrm{I}_{x}^{\mu } \{x^\alpha L_n^{(\alpha )}(x)\}=h_n^{\alpha ,-\mu }\,x^{\alpha +\mu }\, L_n^{(\alpha +\mu )}(x). \end{aligned}$$

Then, performing ${{}_{0}}\mathrm{D}_{x}^{\mu }$ on both sides and taking $\alpha +\mu \rightarrow \alpha ,$ we derive from the relation (2.7) that for $\alpha -\mu >-1,$

$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{\mu } \{x^{\alpha } L_n^{(\alpha )}(x)\}= \frac{1}{h_n^{\alpha -\mu ,-\mu }} x^{\alpha -\mu } L_n^{(\alpha -\mu )}(x)=\frac{\Gamma (n+\alpha +1)}{\Gamma (n+\alpha -\mu +1)} x^{\alpha -\mu } L_n^{(\alpha -\mu )}(x). \end{aligned}$$

This leads to (2.43).

We now turn to (2.44)–(2.45). According to [20, (6.146), P. 191 ] (or [21, (B-7.2), P. 307]), we have

$$\begin{aligned} {}_{x}\mathrm{I}_{\infty }^{\mu } \{e^{-x} L_n^{(\alpha +\mu )}(x)\}= e^{-x} L_n^{(\alpha )}(x),\quad \alpha>-1,~\mu >0. \end{aligned}$$

Similarly, from the property: ${{}_{x}}\mathrm{D}_{\infty }^{\mu } {}_{x}\mathrm{I}_{\infty }^{\mu }\, u(x)=u(x),$ we derive

$$\begin{aligned} {{}_{x}}\mathrm{D}_{\infty }^{\mu } \{ e^{-x} L_n^{(\alpha )}(x)\}=e^{-x} L_n^{(\alpha +\mu )}(x). \end{aligned}$$

Finally, we prove (2.46). Noting that

$$\begin{aligned} _1F_1(a;c; x)=e^x~ _1F_1(c-a;c; -x), \end{aligned}$$

(A.2)

(cf. [2, P. 191]), we derive from (2.34) and (A.2) that

$$\begin{aligned}&x^\alpha L_{n}^{(\alpha )}(x)e^{-x}= x^\alpha \frac{(\alpha +1)_n}{n!}~{}_1F_1\big (-n;\alpha +1;x\big )e^{-x}\nonumber \\&\quad =\frac{(\alpha +1)_n}{n!}x^\alpha ~{}_1F_1\big (n+\alpha +1;\alpha +1;-x\big ) =\frac{(\alpha +1)_n}{n!}x^\alpha ~{}_1F_1\big (n+\alpha +1;\alpha +1;-x\big )\nonumber \\&\quad =\frac{(\alpha +1)_n}{n!}\sum _{j=0}^\infty \frac{(n+\alpha +1)_j(-1)^j}{(\alpha +1)_j}\frac{x^{j+\alpha }}{j!}. \end{aligned}$$

(A.3)

Then acting the derivative ${{}_{}}\mathrm{D}_{}^{k}$ on (A.3) and using the identities (2.34), (A.2) again, we obtain

$$\begin{aligned}\begin{aligned} {{}_{}}\mathrm{D}_{}^{k} \big \{x^\alpha L_{n}^{(\alpha )} (x)e^{-x}\big \}&=\frac{(\alpha +1)_n}{n!}\sum _{j=0}^\infty \frac{(n+\alpha +1)_j(-1)^j}{(\alpha +1)_j}\frac{{{}_{}}\mathrm{D}_{}^{k} x^{j+\alpha }}{j!}\\&=\frac{(\alpha +1)_n}{n!}\sum _{j=0}^\infty \frac{(n+\alpha +1)_j(-1)^j}{(\alpha +1)_j}\frac{\Gamma (j+\alpha +1)}{\Gamma (j+\alpha -k+1)}\frac{ x^{j+\alpha -k}}{j!}\\&=x^{\alpha -k}\frac{(\alpha +1)_n}{n!}\frac{\Gamma (\alpha +1)}{\Gamma (\alpha -k+1)}\sum _{j=0}^\infty \frac{(n+\alpha +1)_j}{(\alpha -k+1)_j}\frac{ (-x)^{j}}{j!}\\&=x^{\alpha -k}\frac{(\alpha -k+1)_{n+k}}{n!}{}_1F_1\big (n+\alpha +1; \alpha -k+1;-x\big )\\&=\frac{(n+k)!}{n!}x^{\alpha -k}\frac{(\alpha -k+1)_{n+k}}{(n+k)!} {}_1F_1\big (-n-k;\alpha -k+1;x\big )e^{-x}\\&=\frac{\Gamma (n+k+1)}{\Gamma (n+1)}x^{\alpha -k}L^{(\alpha -k)}_{n+k}(x) e^{-x}.\\ \end{aligned}\end{aligned}$$

This ends the proof.

Appendix B: Derivation of (5.28) and the Entries of ${\mathbf {A}}$

Derivation of (5.28)

• for $x\in {\mathbb {R}}^-$, $0<s<1$,

  $$\begin{aligned} \begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{*}(x)&={}_{-\infty }\mathrm{I}_{x}^{1-s,\lambda }{{}_{-\infty }}\mathrm{D}_{x}^{1,\lambda } \phi ^{*}(x)=\frac{e^{-\lambda x}}{\Gamma (1-s)}\int _{-\infty } ^x\frac{e^{\lambda \tau }(2\lambda )e^{\lambda \tau }}{(x-\tau )^s} \mathrm{d}\tau \\&\overset{t=x-\tau }{=}\frac{2\lambda e^{-\lambda x}}{\Gamma (1-s)}\int _0^{\infty }\frac{e^{2\lambda (x-t)}}{t^s} \mathrm{d}t =\frac{(2\lambda )^{s}e^{\lambda x}}{\Gamma (1-s)}\int _0^{\infty } e^{-2\lambda t}(2\lambda t)^{-s} \mathrm{d}(2\lambda t)\\&=(2\lambda )^{s}e^{\lambda x},\\ {{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{-}_{n_1}(x)&={}_{-\infty }\mathrm{I}_{x}^{1-s,\lambda } {{}_{-\infty }}\mathrm{D}_{x}^{1,\lambda }\phi ^-_{n_1}(x)\overset{(3.10)}{=}{}_{-\infty }\mathrm{I}_{x}^{1-s,\lambda }\{-({n_1}+1){\mathcal {L}}^{(0,\lambda )}_{{n_1}+1}{(-x)}\}\\&\overset{(2.44)}{=}-({n_1}+1)(2\lambda ) ^{s-1}L^{(s-1)}_{{n_1}+1}{(-2\lambda x)}e^{-\lambda x}\\ {{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{+}_{n_2}(x)&=0 \end{aligned} \end{aligned}$$

  (B.1)

• for $x\in {\mathbb {R}}^+$, $0<s<1$,

  $$\begin{aligned} \begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{*}(x)&={}_{-\infty }\mathrm{I}_{x}^{1-s,\lambda } {{}_{-\infty }}\mathrm{D}_{x}^{1,\lambda }\phi ^{*}(x){=}\frac{e^{-\lambda x}}{\Gamma (1-s)}\int _{-\infty }^0\frac{2\lambda e^{2\lambda \tau }}{(x-\tau )^s} \mathrm{d}\tau \overset{\tau =x-t}{=}\frac{2\lambda e^{\lambda x}}{\Gamma (1-s)}\\&\quad \int _x^{\infty }\frac{ e^{-2\lambda t}}{t^s} \mathrm{d}t,\\ {{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{-}_{n_1}(x)&={}_{-\infty }\mathrm{I}_{x}^{1-s,\lambda } {{}_{-\infty }}\mathrm{D}_{x}^{1,\lambda }\phi ^{-}_{n_1}(x)\overset{(3.10)}{=} \frac{e^{-\lambda x}}{\Gamma (1-s)}\\&\int _{-\infty }^0\frac{-(n_1+1) L^{(0)}_{{n_1}+1}{(-2\lambda \tau )}e^{2\lambda \tau }}{(x-\tau )^s} \mathrm{d}\tau \\&\overset{\tau =x-t}{=}-e^{\lambda x}\frac{{n_1}+1}{\Gamma (1-s)} \int _x^{\infty }\frac{L^{(0)}_{{n_1}+1}{(2\lambda (t-x))}e^{-2\lambda t}}{t^s} \mathrm{d}t,\\ {{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{+}_{n_2}(x)&={}_{-\infty }\mathrm{I}_{x}^{1-s,\lambda }{{}_{-\infty }}\mathrm{D}_{x}^{1,\lambda }\phi ^{+}_{n_2}(x)\overset{(3.9)}{=}\frac{e^{-\lambda x}}{\Gamma (1-s)}\int _0^{x}\frac{({n_2}+1)L^{(0)}_{{n_2}}{(x)}}{(x-\tau )^s} \mathrm{d}\tau \\&=\frac{\Gamma (n_2+2)}{\Gamma (n_2+2-s)}x^{1-s}{\mathcal {L}}^{(1-s,\lambda )}_{{n_2}}{(x)}. \end{aligned} \end{aligned}$$

  (B.2)

The entries of matrix ${\mathbf {A}}$ with $1<\mu =1+s<2$.

$$\begin{aligned} \begin{aligned} \big ({{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{*},&{{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }\phi ^{*}\big ) =\frac{-(2\lambda )^2}{\Gamma (1-s)}\int _0^\infty \int _x^{\infty } \frac{ e^{-2\lambda t}}{t^s} \mathrm{d}t\mathrm{d}x=\frac{-(2\lambda )^2}{\Gamma (1-s)}\int _0^\infty \frac{ e^{-2\lambda t}}{t^s} \int _0^{t}1 \mathrm{d}x\mathrm{d}t\\&=\frac{-(2\lambda )^2}{\Gamma (1-s)}\int _0^\infty {t^{1-s}}{ e^{-2\lambda t}} \mathrm{d}t\overset{\tau =2\lambda t}{=}\frac{-(2\lambda )^{s}}{\Gamma (1-s)} \int _0^\infty {\tau ^{1-s}}{ e^{-\tau }}\mathrm{d}\tau {=}(s-1)(2\lambda )^{s}. \end{aligned} \end{aligned}$$

(B.3)

Since

$$\begin{aligned} {{}_{}}\mathrm{D}_{}^{}\big \{(2\lambda x)L^{(1)}_{n_2+1}(2\lambda x)\big \}= & {} 2\lambda (n_2+2) L^{(0)}_{n_2+1}(2\lambda x),~ \text {i.e.} ~\int _0^{t} L^{(0)}_{n_2+1}(2\lambda x)\mathrm{d}x\\= & {} \frac{1}{n_2+2} tL^{(1)}_{n_2+1}(2\lambda t), \end{aligned}$$

then,

$$\begin{aligned} \begin{aligned} \big ({{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{*},{{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }\phi ^+_{n_2}\big )&=\frac{-2\lambda (n_2+1)}{\Gamma (1-s)}\int _0^\infty \int _x^{\infty } \frac{ e^{-2\lambda t}}{t^s} \mathrm{d}t~ L^{(0)}_{n_2+1}(2\lambda x)\mathrm{d}x\\&{=}\frac{-2\lambda (n_2+1)}{\Gamma (1-s)}\int _0^\infty \frac{ e^{-2\lambda t}}{t^s}\int _0^{t}L^{(0)}_{n_2+1}(2\lambda x) \mathrm{d}x~ \mathrm{d}t\\&{=}\frac{-2\lambda (n_2+1)}{(n_2+2)\Gamma (1-s)}\int _0^\infty t^{1-s}L^{(1)} _{n_2+1}(2\lambda t)e^{-2\lambda t} \mathrm{d}t. \end{aligned} \end{aligned}$$

(B.4)

Similarly, we have

$$\begin{aligned}&\big ({{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{-}_{n_1},{{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }\phi ^{+}_{n_2}\big )\nonumber \\&\quad {=}\frac{({n_1}+1)({n_2}+1)}{\Gamma (1-s)}\int _0^\infty \int _x^{\infty }\frac{L^{(0)}_{{n_1}+1}{(2\lambda (t-x))} e^{-2\lambda t}}{t^s} \mathrm{d}t ~L^{(0)}_{n_2+1}(2\lambda x) \mathrm{d}x\nonumber \\&\quad {=} \frac{({n_1}+1)({n_2}+1)}{\Gamma (1-s)}\int _0^\infty {t^{-s}}e^{-2\lambda t} \int _0^{t}~L^{(0)}_{n_2+1}(2\lambda x)L^{(0)}_{{n_1}+1}{(2\lambda (t-x))} \mathrm{d}x \mathrm{d}t\nonumber \\&\quad \overset{x=t\xi }{=} \frac{({n_1}+1)({n_2}+1)}{\Gamma (1-s)} \int _0^\infty {t^{1-s}}e^{-2\lambda t} \int _0^{1}~ L^{(0)}_{n_2+1} (2\lambda t\xi )L^{(0)}_{{n_1}+1}{(2\lambda t(1-\xi ))} \mathrm{d}\xi \mathrm{d}t.\nonumber \\ \end{aligned}$$

(B.5)

The entries of matrix ${\mathbf {A}}$ with $0<\mu =s<1$.

$$\begin{aligned} \begin{aligned}&\big ({{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{*},\phi ^{*}\big )=(2\lambda )^s\int _{-\infty }^0e^{2\lambda x} \mathrm{d}x+\frac{2\lambda }{\Gamma (1-s)}\int _0^\infty \int _x^{\infty }\frac{ e^{-2\lambda t}}{t^s} \mathrm{d}t\mathrm{d}x \\ {}&=(2\lambda )^{s-1}+\frac{2\lambda }{\Gamma (1-s)}\int _0^\infty \frac{ e^{-2\lambda t}}{t^s} \int _0^{t}1 \mathrm{d}x\mathrm{d}t=(2\lambda )^{s-1}+\frac{2\lambda }{\Gamma (1-s)}\int _0^\infty {t^{1-s}}{ e^{-2\lambda t}}\mathrm{d}t\\&\overset{\tau =2\lambda t}{=}(2\lambda )^{s-1}+\frac{(2\lambda )^{s-1}}{\Gamma (1-s)}\int _0^\infty {\tau ^{1-s}}{ e^{-\tau }}\mathrm{d}\tau =(2-s)(2\lambda )^{s-1}. \end{aligned} \end{aligned}$$

(B.6)

Owing to

$$\begin{aligned} {{}_{}}\mathrm{D}_{}^{}\big \{(2\lambda x)^2L^{(2)}_{n_2}(2\lambda x)\big \}=(2\lambda )^2(n_2+2) xL^{(1)}_{n_2}(2\lambda x), \end{aligned}$$

i.e.,

$$\begin{aligned} \int _0^{t} xL^{(1)}_{n_2}(2\lambda x)\mathrm{d}x=\frac{1}{n_2+2} t^2L^{(2)}_{n_2}(2\lambda t), \end{aligned}$$

we obtain that

$$\begin{aligned} \begin{aligned}&\big ({{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{*},\phi ^+_{n_2}\big ) =\int _0^\infty \frac{e^{-\lambda x}}{\Gamma (1-s)}\int _{-\infty }^0\frac{2 \lambda e^{2\lambda \tau }}{(x-\tau )^s} \mathrm{d}\tau ~ xL^{(1)}_{n_2} (2\lambda x)e^{-\lambda x} \mathrm{d}x\\&\overset{\tau =x-t}{=}\frac{2\lambda }{\Gamma (1-s)}\int _0^\infty \int _x^{\infty }\frac{ e^{-2\lambda t}}{t^s} \mathrm{d}t~ xL^ {(1)}_{n_2}(2\lambda x)\mathrm{d}x{=}\frac{2\lambda }{\Gamma (1-s)}\\&\quad \int _0^\infty \frac{ e^{-2\lambda t}}{t^s}\int _0^{t}xL^{(1)}_{n_2} (2\lambda x) \mathrm{d}x~ \mathrm{d}t\\&\quad {=}\frac{2\lambda }{(n_2+2)\Gamma (1-s)}\int _0^\infty t^{2-s}L^{(2)}_{n_2}(2\lambda t)e^{-2\lambda t} \mathrm{d}t. \end{aligned} \end{aligned}$$

(B.7)

Similarly, we have

$$\begin{aligned} \begin{aligned} \big ({{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{-}_{n_1},\phi ^{+}_{n_2}\big )&{=} -\frac{{n_1}+1}{\Gamma (1-s)}\int _0^\infty \int _x^{\infty }\frac{L^{(0)} _{{n_1}+1}{(2\lambda (t-x))}e^{-2\lambda t}}{t^s} \mathrm{d}t ~xL^{(1)}_ {n_2}(2\lambda x) \mathrm{d}x\\&{=}-\frac{{n_1}+1}{\Gamma (1-s)}\int _0^\infty {t^{-s}}e^{-2\lambda t} \int _0^{t}~xL^{(1)}_{n_2}(2\lambda x)L^{(0)}_{{n_1}+1}{(2\lambda (t-x))} \mathrm{d}x \mathrm{d}t\\&\overset{x=t\xi }{=}-\frac{{n_1}+1}{\Gamma (1-s)}\int _0^\infty {t^{2-s}}e^{-2\lambda t} \int _0^{1}~\xi L^{(1)}_{n_2}(2\lambda t\xi )L^{(0)}_{{n_1}+1}{(2\lambda t(1-\xi ))} \mathrm{d}\xi \mathrm{d}t\\ \end{aligned}\nonumber \\ \end{aligned}$$

(B.8)

The above equations are enough to calculate out the matrix ${\mathbf {A}}$ due to some symmetric properties of the entries.