Frozen Gaussian Approximation-Based Artificial Boundary Conditions for One-Dimensional Nonlinear Schrödinger Equation in the Semiclassical Regime

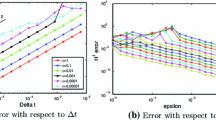
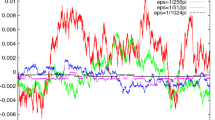
Abstract

In this paper, we first analyze the stability of the unified approach, proposed in Zhang et al. (Phys Rev E 78:026709, 2008), for the nonlinear Schödinger equation in the semiclassical regime. The analysis shows that small semiclassical parameters deteriorate the accuracy of the unified approach, which will be also verified by numerical examples. Motivated by the time-splitting spectral method (Bao et al. in SIAM J Sci Comput 25:27–64, 2003), we generalize our previous work (Yang and Zhang in SIAM J Numer Anal 52:808–831, 2014), and propose frozen Gaussian approximation (FGA)-based artificial boundary conditions for solving one-dimensional nonlinear Schrödinger equation on unbounded domain. We split the linear part of the Schrödinger equation from the nonlinear part, and deal with the artificial boundary condition of the linear part by a simple strategy that all the Gaussian functions, whose dynamics are governed by the Hamiltonian flows, going out of the domain will be eliminated numerically. Since the nonlinear part is given by ordinary differential equations, it does not require artificial boundary conditions and can be solved directly. This strategy also works for the nonlinear Schrödinger equation with periodic lattice potential by using Bloch decomposition-based FGA. We present numerical examples to verify the performance of proposed numerical methods.

Appendix: FGA-Base Strang-Splitting Method for Periodic Potentials

We consider the nonlinear Schrödinger equation with a periodic potential in one-dimension,

$$\begin{aligned} \mathrm {i}\varepsilon \partial _{t}\psi ^{\varepsilon }=-\dfrac{\varepsilon ^{2}}{2}\partial _{xx} \psi ^{\varepsilon }+V_{\Gamma }(x/\varepsilon )\psi ^{\varepsilon }+f(|\psi ^{\varepsilon }|^{2})\psi ^{\varepsilon },\quad x\in \mathbb {R}. \end{aligned}$$

(5.1)

The potential $V_{\Gamma }(x)$ is periodic with respect to $\Gamma =[0,2\pi )$ so that $V(x/\varepsilon )$ is highly oscillatory for $\varepsilon \ll 1$. Note that unlike (1.1), Eq. (5.1) has a factor of 1 / 2 infront of the Laplacian term. One can easily modify our previous algorithms to deal with such trivial scaling of the Hamiltonian. We leave the factor of 1 / 2 to be consistent with the work presented in [43] and [44]. The splitting algorithm described by Eqs. (3.18 3.19)–(3.20) will be used, with the main difference coming from $V(x)=V_{\Gamma }(x/\varepsilon )$ is now periodic.

For certain potentials, the eigenfunctions for the Hamiltonian operator for the Linear Schrödinger are known. It is to our advantage to make use of this fact as diagonalization of the Linear Schrödinger equation can yield “exact” solutions. One example where diagonalization is possible is the case of periodic potentials (assumed to be smooth for simplicity). This is done using Bloch’s Theorem, thus we diagonalize the linear part of (5.1) using the Bloch-decomposition based FGA (see [43, 44]).

Remark 1

If we include an external potential in Eq. (5.1), It is still possible to obtain an asymptotic solution to the linear part of (5.1) using basis functions which diagonalize the periodic part of the Hamiltonian. This is done in [43, 44] where external potentials are also considered.

We now summarize the Bloch-decomposition-based FGA. The Bloch-decomposition FGA proposes to solve

$$\begin{aligned} \mathrm {i}\varepsilon \partial _{t}\psi ^{\varepsilon }=-\dfrac{\varepsilon ^{2}}{2}\partial _{xx}\psi ^{\varepsilon }+V_{\Gamma }\left( \dfrac{x}{\varepsilon }\right) \psi ^{\varepsilon }+U(x)\psi ^{\varepsilon } \end{aligned}$$

(5.2)

where $\psi ^{\varepsilon }\in L^{2}(\mathbb {R})$ is an asymptotic solution with $L^{2}(\mathbb {R})$ initial condition. This is done by diagonalization of the periodic part of the Hamiltonian operator using Bloch waves. Bloch waves are the eigenfunctions $u_{n}(\xi ,x)$ with corresponding eigenvalues $E_{n}(\xi )$ of the (compact) operator

$$\begin{aligned} H_{\xi }:=\dfrac{1}{2}(-\mathrm {i}\partial _{x}+\xi )^{2}+V_{\Gamma }(x). \end{aligned}$$

(5.3)

In the above equation, $\xi$ takes any value in $[-\pi ,\pi )$ and $n\in 1,2,\ldots$, with $u_{n}(\xi ,x)$ normalized to unity with respect to x so that

$$\begin{aligned} \int _{[0,1)}|u_{n}(\xi ,x)|^{2}dx=1. \end{aligned}$$

(5.4)

We use periodic boundary conditions for Eq. (5.3) and we also extend $u_{n}(\xi ,x)$ periodically with respect to x on $\mathbb {R}$. Numerical implementation of Bloch eigenvalues and eigenfunctions in one dimension is referred to [44]. We summarize the Bloch-based FGA solution to Eq. (5.1) below,

$$\begin{aligned} \psi _{\mathrm {FGA}}^{\varepsilon }(t, x)= & {} \frac{1}{(2\pi \varepsilon )^{3/2}}\sum _{n=0}^{\infty } \int _{\Gamma }\int _{\mathbb {R}} a_{n}(t, q, p) e^{\mathrm {i}S_n (t,q,p) / \varepsilon } G^{\varepsilon }_{{Q}_n, P_n}(x) u_n(P_n, x/ \varepsilon )\nonumber \\&\times \left( \int _{{\mathbb {R}}}{\overline{G}^{\varepsilon }_{q, p}(y) \overline{u}_n(p, y / \varepsilon ) \psi _0^{\varepsilon }(y)}\mathrm {d}y\right) \mathrm {d}q \mathrm {d}p, \end{aligned}$$

(5.5)

where the evolution of $({Q}_{n},P_{n},S_{n},a_{n})$ is governed by

$$\begin{aligned} \dfrac{\partial Q_{n}}{\partial t}= & {} \partial _{P_{n}}h_{n}(Q_{n},P_{n}),\nonumber \\ \dfrac{\partial P_{n}}{\partial t}= & {} -\partial _{Q_{n}}h_{n}(Q_{n},P_{n}),\nonumber \\ \dfrac{\partial S_{n}}{\partial t}= & {} P_{n}\cdot \partial _{P_{n}} h_{n}(Q_{n},P_{n})-h_{n}(Q_{n},P_{n}),\nonumber \\ \dfrac{\partial a_{n}}{\partial t}= & {} -\mathrm {i}a_{n}\mathcal {A}_{n}\cdot \partial U(Q_{n})+\dfrac{1}{2}a_{n}\left( \partial _{{z}}P_{n}\, E''(P_{n}) \bigl (Z_{n}\bigr )^{-1}\right) \nonumber \\&-\dfrac{\mathrm {i}}{2}a_{n}\left( \partial _{{z}}Q_{n}\,U''(Q_{n})\bigl (Z_{n}\bigr )^{-1}\right) . \end{aligned}$$

(5.6)

where $\mathcal {A}_{n}:=\langle u_{n}(x,\xi ),\partial u_{n}(x,\xi )\rangle$ and the classical Hamiltonian $h_{n}$ is given by $h_{n}(q,p)=E_{n}(p)\,+\,U(q)$. The initial conditions are $Q_{n}(0,q,p)=q$, $P_{n}(0,q,p)=p$, $S_{n}(0,q,p)=0$, and ${a_{n}(0,q,p)=2^{1/2}}$.

Remark 2

In the case that $U(x)\ne 0$ (or a constant), an asymptotic solution to Eq. (5.5) by diagonalization using Bloch waves is numerically a more delicate problem. This is because the eigenfunctions of (5.3) are defined up to a unit complex number so that $\widetilde{u}_{n}(\xi ,x)=e^{\mathrm {i}\phi (\xi )}u_{n}(\xi ,x)$ also provides a set of Bloch waves. In this case, $\mathcal {A}_{n}$ will not be well defined. In order to avoid numerical difficulties, one can use a Gauge-invariant algorithm described in [44].

Accuracy for the Bloch-Based Time-Splitting FGA Algorithm

Because of the Bloch-decomposition, we introduce extra errors in computing (5.1). Using an integrator of order p to solve the Hamiltonian equations (5.6), the total error is

$$\begin{aligned} \mathcal {O}\left( \varepsilon +\delta t+\dfrac{\delta t^{p}}{\varepsilon }\right) +\left| \left| \psi _{0}^{\varepsilon }-\sum _{n=1}^{N}\prod _{n}\psi _{0}^{\varepsilon }\right| \right| _{L^{2}} \end{aligned}$$

(5.7)

where $\prod _{n}f$ is the projection of f onto the nth band space. The last term of (5.7) is the error that is propagated by the initial decomposition of $\psi _{0}^{\varepsilon }$ using the first N Bloch bands.

Remark 3

In general, the numerical cost of computing Bloch waves drastically increases as the dimensionality of the problem increases. Another major difficulty arising by using Bloch decomposition is due to the possibility of band crossings. This happens whenever the distance of the eigenvalue $E_{n}(\xi )$ to any other eigenvalue $E_{m}(\xi )$ is very small. In this case, the gradient of $E_{n}(\xi )$ may not be well defined. Because band crossings are more prevalent in higher dimensions, our last example will be in 1-dimension.

Example 5.1

(Bloch eigenvalues and eigenfunctions) We compute the first few lowest energy eigenvalues and eigenfunctions to Eq. (5.3) for the periodic potential

$$\begin{aligned} V_{\Gamma }(x)=\exp (-25(x-\pi )^{2}) \end{aligned}$$

(5.8)

extended periodically with respect to $[0,2\pi )$. Figure 3 displays the 8 lowest energy eigenvalues and Fig. 4 displays the absolute value of the first 4 lowest energy eigenfunctions. Despite the fact that the periodic extension is not analytic on 0 and $2\pi$, this poses no problem numerically because of the rapid decay of the exponential function. Because we cannot preform the infinite summation of Eq. (5.5) numerically, our last example approximates $\psi ^{\varepsilon }(t,x)$ by summing over the first 8 lowest energy band spaces.

Fig. 3

Energy eigenvalues for the one-dimensional lattice potential $V_{\Gamma }(x)=\exp \left( -\,25x^{2}\right)$

Fig. 4

Module of eigenfunctions for the one-dimensional lattice potential $V_{\Gamma }(x)=\exp \left( -\,25x^{2}\right)$. We display absolute value of the first 4 lowest energy eigenfunctions

Example 5.2

(Schrödinger with periodic potential) We choose the initial condition and nonlinearity as

$$\begin{aligned} \psi _0(x)=\exp (-25x^2), \quad f(x)=x. \end{aligned}$$

(5.9)

We take the potential to be $V_{\Gamma }(x/\varepsilon )$ where $V_{\Gamma }(x)=\exp (-x^{2})$ is extended periodically with respect to the lattice ${\Gamma }$. We also note that the periodic extension of $V_{\Gamma }(x)$ poses no numerical problem due to the rapid decay of the exponential function. Comparisons are shown in Fig. 5 where one can see that the Bloch-based time-splitting FGA algorithm approximates the solution with good accuracy.

Fig. 5

Plot of $\mathfrak {R}[\psi _{ex}]$ and $Re[\psi _{FGA}]$ and $\mathfrak {R}[\psi _{ex}-\psi _{FGA}]$ for $\varepsilon =1/16$ for Example 5.2