Skip to main content
SpringerLink
Log in

Maximum-Principle-Satisfying and Positivity-Preserving High Order Central DG Methods on Unstructured Overlapping Meshes for Two-Dimensional Hyperbolic Conservation Laws

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

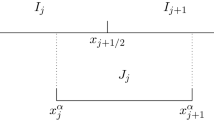
In this paper, we first present a family of high order central discontinuous Galerkin methods defined on unstructured overlapping meshes for the two-dimensional conservation laws. The primal mesh is a triangulation of the computational domain, while the dual mesh is a quadrangular partition which is formed by connecting an interior point and the three vertexes of each triangle on the primal mesh. We prove the \(L^2\) stability of the present method for linear equation. Then we design and analyze high order maximum-principle-satisfying central discontinuous Galerkin methods for two-dimensional scalar conservation law, and high order positivity-preserving central discontinuous Galerkin methods for two-dimensional compressible Euler systems. The performance of the proposed methods is finally demonstrated through a set of numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Brio, M., Zakharian, A.R., Webb, G.M.: Two-dimensional Riemann solver for Euler equations of gas dynamics. J. Comput. Phys. 167, 177–195 (2001)

    Article  MATH  Google Scholar 

  2. Chen, G., Feng, M.: Stabilized finite element methods for the Biot’s consolidation problem. Adv. Appl. Math. Mech. 10, 77–99 (2018)

    Article  MathSciNet  Google Scholar 

  3. Chen, G., Hu, W.W., Shen, J.G., Singler, J.R., Zhang, Y.W., Zheng, X.B.: An HDG method for distributed control of convection diffusion PDEs. J. Comput. Appl. Math. 343, 643–661 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  4. Chen, Y., Luo, Y., Feng, M.: Analysis of a discontinuous Galerkin method for the Biot’s consolidation problem. Appl. Math. Comput. 219, 9043–9056 (2013)

    MathSciNet  MATH  Google Scholar 

  5. Cheng, Y., Li, F., Qiu, J., Xu, L.: Positivity-preserving DG and central DG methods for ideal MHD equations. J. Comput. Phys. 238, 255–280 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. Cockburn, B., Lin, S.-Y., Shu, C.-W.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one-dimensional systems. J. Comput. Phys. 84, 90–113 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  7. Cockburn, B., Shu, C.-W.: The Runge–Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J. Comput. Phys. 141, 199–224 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  8. Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics. Springer, Berlin (2000)

    Book  MATH  Google Scholar 

  9. Deng, X.-L., Li, M.: Simulating compressible two-medium flows with sharp-interface adaptive Runge–Kutta discontinuous Galerkin methods. J. Sci. Comput. 74, 1347–1368 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  10. Dong, H., Li, M.: A reconstructed central discontinuous Galerkin-finite element method for the fully nonlinear weakly dispersive Green–Naghdi model. Appl. Numer. Math. 110, 110–127 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  11. Dong, H., Lv, M., Li, M.: A reconstructed central discontinuous Galerkin method for conservation laws. Comput. Fluids 153, 76–84 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability preserving high order time discretization methods. SIAM Rev. 43, 89–112 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  13. Jiang, G.-S., Shu, C.-W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kim, H.H., Chung, E.T., Lee, C.S.: A staggered discontinuous Galerkin method for the Stokes system. SIAM J. Numer. Anal. 51, 3327–3350 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. Li, F., Yakovlev, S.: A central discontinuous Galerkin method for Hamilton–Jacobi equations. J. Sci. Comput. 45, 404–428 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  16. Li, F., Xu, L.: Arbitrary order exactly divergence-free central discontinuous Galerkin methods for ideal MHD equations. J. Comput. Phys. 231, 2655–2675 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Li, F., Xu, L., Yakovlev, S.: Central discontinuous Galerkin methods for ideal MHD equations with exactly divergence-free magnetic field. J. Comput. Phys. 230, 4828–4847 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Li, M., Guyenne, P., Li, F., Xu, L.: High order well-balanced CDG-FE methods for shallow water waves by a Green-Naghdi model. J. Comput. Phys. 257, 169–192 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Li, M., Chen, A.: High order central discontinuous Galerkin-finite element methods for the Camassa–Holm equation. Appl. Math. Comput. 227, 237–245 (2014)

    MathSciNet  MATH  Google Scholar 

  20. Li, M., Li, F.Z., Xu, L.: Maximum-principle-satisfying and positivity-preserving high order CDG methods for conservation laws. SIAM J. Sci. Comput. 38, A3720–A3740 (2016)

    Article  MATH  Google Scholar 

  21. Li, M., Guyenne, P., Li, F., Xu, L.: A positivity-preserving well-balanced central discontinuous Galerkin method for the nonlinear shallow water equations. J. Sci. Comput. 711, 994–1034 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, M., Jiang, Y., Dong, H.: High order well-balanced central local discontinuous Galerkin-finite element methods for solving the Green–Naghdi model. Appl. Math. Comput. 315, 113–130 (2017)

    MathSciNet  Google Scholar 

  23. Li, X.: Boundedness in a two-dimensional attraction-repulsion system with nonlinear diffusion. Math. Methods Appl. Sci. 39, 289–301 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Liu, Y., Shu, C.-W., Tadmor, E., Zhang, M.: Central discontinuous Galerkin methods on overlapping cells with a nonoscillatary hierarchical reconstruction. SIAM J. Numer. Anal. 45, 2442–2467 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  25. Liu, Y., Shu, C.-W., Tadmor, E., Zhang, M.: Central local discontinuous Galerkin methods on overlapping cells for diffusion equations. ESAIM: Math. Model. Numer. Anal. 45, 1009–1032 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. Luo, Y., Feng, M., Xu, Y.: A stabilized mixed discontinuous Galerkin method for the incompressible miscible displacement problem. Bound. Value Probl. 2011, 48 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Technical Report LA-UR-73-479, Los Alamos Scientific Laboratory (1973)

  28. Ren, X., Wu, J., Xiang, Z., Zhang, Z.: Global existence and decay of smooth solution for the 2-D MHD equation without magnetic diffusion. J. Funct. Anal. 267, 503–541 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  29. Shu, C.-W.: Essentially Non-oscillatory and Weighted Essentially Non-oscillatory Schemes for Hyperbolic Conservation Laws, ICASE Report. Brown University, Rhode Island (1997)

    Google Scholar 

  30. Sun, M., Takayama, K.: The formation of a secondary shock wave behind a shock wave diffracting at a convex corner. Shock Waves 7, 287–295 (1997)

    Article  MATH  Google Scholar 

  31. Tang, H., Warnecke, G.: A Runge–Kutta discontinuous Galerkin method for the Euler equations. Comput. Fluids 34, 375–398 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  32. Vukovic, S., Sopta, L.: ENO and WENO schemes with the exact conservation property for one-dimensional shallow water equations. J. Comput. Phys. 179, 593–621 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  33. Wang, C., Zhang, X., Shu, C.-W., Ning, J.: Robust high order discontinuous Galerkin schemes for two-dimensional gaseous detonations. J. Comput. Phys. 231, 653–665 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  34. Xu, Z., Liu, Y.: New central and central discontinuous Galerkin schemes on overlapping cells of unstructured grids for solving ideal magnetohydrodynamic equations with globally divergence-free magnetic field. J. Comput. Phys. 327, 203–224 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  35. Zhang, X., Shu, C.-W.: On maximum-principle-satisfying high order schemes for scalar conservation laws. J. Comput. Phys. 229, 3091–3120 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  36. Zhang, X., Shu, C.-W.: On positivity-preserving high order discontinuous Galerkin schemes for compressible Euler equations on rectangular meshes. J. Comput. Phys. 229, 8918–8934 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  37. Zhang, X., Xia, Y., Shu, C.-W.: Maximum-principle-satisfying and positivity-preserving high order discontinuous Galerkin schemes for conservation laws on triangular meshes. J. Sci. Comput. 50, 29–62 (2012)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

ML is partially supported by a NSFC (Grant No. 11501062, 11871139). HD is partially supported by a NSFC (Grant No. 11701055). LX is partially supported by a Key Project of the Major Research Plan of NSFC (Grant No. 91630205) and a NSFC (Grant No. 11771068).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, 611731, Sichuan, People’s Republic of China

    Maojun Li & Liwei Xu

  2. College of Mathematics and Statistics, Chongqing University, Chongqing, 401331, People’s Republic of China

    Haiyun Dong & Binbin Hu

Authors
  1. Maojun Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haiyun Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Binbin Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Liwei Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Liwei Xu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, M., Dong, H., Hu, B. et al. Maximum-Principle-Satisfying and Positivity-Preserving High Order Central DG Methods on Unstructured Overlapping Meshes for Two-Dimensional Hyperbolic Conservation Laws. J Sci Comput 79, 1361–1388 (2019). https://doi.org/10.1007/s10915-018-00895-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-00895-x

Keywords

Mathematics Subject Classification

Search

Navigation