Skip to main content
SpringerLink
Log in

WSGD-OSC Scheme for Two-Dimensional Distributed Order Fractional Reaction–Diffusion Equation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

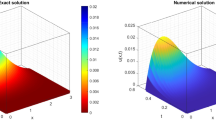
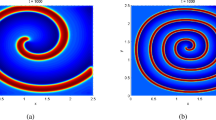
In this paper, a new numerical approximation is discussed for the two-dimensional distributed-order time fractional reaction–diffusion equation. Combining with the idea of weighted and shifted Grünwald difference (WSGD) approximation (Tian et al. in Math Comput 84:1703–1727, 2015; Wang and Vong in J Comput Phys 277:1–15, 2014) in time, we establish orthogonal spline collocation (OSC) method in space. A detailed analysis shows that the proposed scheme is unconditionally stable and convergent with the convergence order \(\mathscr {O}(\tau ^2+\Delta \alpha ^2+h^{r+1})\), where \(\tau , \Delta \alpha , h\) and r are, respectively the time step size, step size in distributed-order variable, space step size, and polynomial degree of space. Interestingly, we prove that the proposed WSGD-OSC scheme converges with the second-order in time, where OSC schemes proposed previously (Fairweather et al. in J Sci Comput 65:1217–1239, 2015; Yang et al. in J Comput Phys 256:824–837, 2014) can at most achieve temporal accuracy of order which depends on the order of fractional derivatives in the equations and is usually less than two. Some numerical results are also given to confirm our theoretical prediction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Luchko, Y.: Boundary value problems for the generalized time fractional diffusion equation of distributed order. Fract. Calc. Appl. Anal. 12, 409–422 (2009)

    MathSciNet  MATH  Google Scholar 

  2. Luchko, Y.: Maximum principle and its application for the time-fractional diffusion equations. Fract. Calc. Appl. Anal. 14, 110–124 (2011)

    MathSciNet  MATH  Google Scholar 

  3. Li, Z., Luchko, Y., Yamamoto, M.: Asymptotic estimates of solutions to initial-boundary-value problems for distributed order time-fractional diffusion equations. Fract. Calc. Appl. Anal. 17, 1114–1136 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  4. Jia, J., Peng, J., Li, K.: Well-posedness of abstract distributed-order fractional diffusion equations. Commun. Pure Appl. Anal. 13, 605–621 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  5. Meerschaert, M.M., Nane, E., Vellaisamy, P.: Distributed-order fractional diffusions on bounded domains. J. Math. Anal. Appl. 379, 216–228 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. Mainardi, F., Mura, A., Pagnini, G., Gorenflo, R.: Time-fractional diffusion of distributed order. J. Vib. Control 14(9–10), 1267–1290 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  7. Ye, H., Liu, F., Anh, V.: Compact difference scheme for distributed-order time-fractional diffusion-wave equation on bounded domains. J. Comput. Phys. 298, 652–660 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  8. Ye, H., Liu, F., Anh, V., Turner, I.: Numerical analysis for the time distributed-order and Riesz space fractional diffusions on bounded domains. IMA J. Appl. Math. 80, 825–838 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Katsikadelis, J.T.: Numerical solution of distributed order fractional differential equations. J. Comput. Phys. 259, 11–22 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  10. Gao, G.H., Sun, Z.Z.: Two alternating direction implicit difference schemes with the extrapolation method for the two-dimensional distributed-order differential equations. Comput. Math. Appl. 69, 926–948 (2015)

    Article  MathSciNet  Google Scholar 

  11. Gao, G.H., Sun, Z.Z.: Two alternating direction implicit difference schemes for two-dimensional distributed-order fractional diffusion equations. J. Sci. Comput. 66, 1281–1312 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gao, G.H., Sun, H.W., Sun, Z.Z.: Some high-order difference scheme for the distributed-order differential equations. J. Comput. Phys. 298, 337–359 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Du, R., Hao, Z.P., Sun, Z.Z.: Lubich second-order methods for distributed-order time-fractional differential equations with smooth solutions. EAJAM 6, 131–151 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Jin, B., Lazarov, R., Sheen, D., Zhou, Z.: Error estimates for approximations of distributed order time fractional diffusion with nonsmooth data. Fract. Calc. Appl. Anal. 19, 69–93 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  15. Chen, H., Lü, S.J., Chen, W.P.: Finite difference/spectral approximations for the distributed order time fractional reaction–diffusion equation on an unbounded domain. J. Comput. Phys. 315, 84–97 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  16. Morgado, M.L., Rebelo, M.: Numerical approximation of distributed order reaction diffusion equations. J. Comput. Appl. Math. 275, 216–227 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  17. Yan, Y., Fairweather, G.: Orthogonal spline collocation methods for some partial integro-differential equations. SIAM J. Numer. Anal. 29, 755–768 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  18. Bialecki, B., Fairweather, G.: Orthogonal spline collocation methods for partial differential equations. J. Comput. Appl. Math. 128, 55–82 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  19. Bialecki, B., Fairweather, G., López-Marcos, J.C.: The extrapolated Crank–Nicolson orthogonal spline collocation method for a quasilinear parabolic problem with nonlocal boundary conditions. J. Sci. Comput. 62, 265–283 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  20. Fernandes, R.I., Fairweather, G.: An ADI extrapolated Crank–Nicolson orthogonal spline collocation method for nonlinear reaction–diffusion systems. J. Comput. Phys. 231, 6248–6267 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  21. Fernandes, R.I., Bialecki, B., Fairweather, G.: An ADI extrapolated Crank–Nicolson orthogonal spline collocation method for nonlinear reaction–diffusion systems on evolving domains. J. Comput. Phys. 299, 561–580 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Fairweather, G., Yang, X.H., Xu, D., Zhang, H.Z.: An ADI Crank–Nicolson orthogonal spline collocation method for the two-dimensional fractional diffusion-wave equation. J. Sci. Comput. 65, 1217–1239 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  23. Fairweather, G., Zhang, H.Z., Yang, X.H., Xu, D.: A backward Euler orthogonal spline collocation method for the time-fractional Fokker–Plank equation. Numer. Methods Partial Differ. Equ. 31, 1534–1550 (2015)

    Article  MATH  Google Scholar 

  24. Yang, X.H., Zhang, H.X., Xu, D.: Orthogonal spline collocation method for the two-dimensional fractional sub-diffusion equation. J. Comput. Phys. 256, 824–837 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  25. Zhang, H.X., Yang, X.H., Han, X.L.: Discrete-time orthogonal spline collocation method with application to two-dimensional fractional Cable equation. Comput. Math. Appl. 68, 1710–1722 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  26. Tian, W.Y., Zhou, H., Deng, W.H.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84, 1703–1727 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  27. Zhou, H., Tian, W.Y., Deng, W.H.: Quasi-compact finite difference schemes for space fractional diffusion equations. J. Sci. Comput. 56, 45–66 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wang, Z., Vong, S.: Compact difference schemes for the modified anomalous fractional sub-diffusion equation and the fractional diffusion-wave equation. J. Comput. Phys. 277, 1–15 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  29. Percell, P., Wheeler, M.F.: A \(C^1\) finite element collocation method for elliptic equations. SIAM J. Numer. Anal. 17, 605–622 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  30. Fernandes, R.I., Fairweather, G.: Analysis of alternating direction collocation methods for parabolic and hyperbolic problems in two space variables. Numer. Methods Partial Differ. Equ. 9, 191–211 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  31. Greenwell-Yanik, C.E., Fairweather, G.: Analyses of spline collocation methods for parabolic and hyperbolic problems in two space variables. SIAM J. Numer. Anal. 23, 282–296 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  32. Lin, Y.P., Thomée, V., Wahlbin, L.B.: Ritz–Volterra projections to finite-element spaces and applications to integrodifferential and related equations. SIAM J. Numer. Anal. 28, 1047–1070 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  33. Jin, B., Lazarov, R., Liu, Y., Zhou, Z.: The Galerkin finite element method for a multi-term time-fractional diffusion equation. J. Comput. Phys. 281, 825–843 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  34. McLean, W., Mustapha, K.: Time-stepping error bounds for fractional diffusion problems with non-smooth initial data. J. Comput. Phys. 293, 201–217 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  35. Jin, B., Lazarov, R., Pasciak, J., Zhou, Z.: Error analysis of semidiscrete finite element methods for inhomogeneous time-fractional diffusion. IMA J. Numer. Anal. 35, 561–582 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We are grateful to the two anonymous referees for useful comments and suggestions. We also wish to thank Prof. Graeme Fairweather for many useful discussions and for the guidance over the past years.

Author information

Authors and Affiliations

  1. School of Science, Hunan University of Technology, Zhuzhou, 412007, China

    Xuehua Yang & Haixiang Zhang

  2. National Key Laboratory of Science and Technology on Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing, 100088, China

    Xuehua Yang

  3. Department of Mathematics, Hunan Normal University, Changsha, 410081, China

    Da Xu

Authors
  1. Xuehua Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haixiang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Da Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Haixiang Zhang or Da Xu.

Additional information

The work is supported by the National Natural Science Foundation of China Grant 11701168, 11601144, 11626096, 11671131; the Scientific Research Fund of Hunan Provincial Education Department Grant YB2016B033, 16K026; the Science Challenge Project Grant TZ2016002.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, X., Zhang, H. & Xu, D. WSGD-OSC Scheme for Two-Dimensional Distributed Order Fractional Reaction–Diffusion Equation. J Sci Comput 76, 1502–1520 (2018). https://doi.org/10.1007/s10915-018-0672-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-0672-3

Keywords

Mathematics Subject Classification

Search

Navigation