One-Dimensional/Two-Dimensional Coupling Approach with Quadrilateral Confluence Region for Modeling River Systems

Abstract

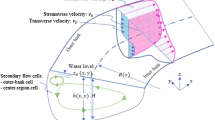
We study shallow water flows in river systems. An accurate description of such flows can be obtained using the two-dimensional (2-D) shallow water equations, which can be numerically solved by a shock-capturing finite-volume method. This approach can, however, be inefficient and computationally unaffordable when a large river system with many tributaries and complex geometry is to be modeled. A popular simplified approach is to model flow in each uninterrupted section of the river (called a reach) as one-dimensional (1-D) and connect the reaches at the river junctions. The flow in every reach can then be modeled using the 1-D shallow water equations, whose numerical solution is dramatically less computationally expensive compared with solving its 2-D counterpart. Even though several point-junction models are available, most of them prove to be sufficiently accurate only in the case of a smooth flow though the junction. We propose a new 1-D/2-D river junction model, in which each reach of the river is modeled by the 1-D shallow water equations, while the confluence region, where the mixing of flows from the different directions occurs, is modeled by the 2-D ones. We define the confluence region to be a trapezoid with parallel vertical sides. This allows us to take into account both the average width of each reach and the angle between the directions of flow of the tributary and the principal river at the confluence. We choose a trapezoidal confluence region as it is consistent with the 1-D model of the river. We implement well-balanced positivity preserving second-order semi-discrete central-upwind schemes developed in Kurganov and Petrova (Commun Math Sci 5:133–160, 2007) for the 1-D shallow water equations and in Shirkhani et al. (Comput Fluids 126: 25–40, 2016) for the 2-D shallow water equations using quadrilateral grids. For the 2-D junction simulations in the confluence region we choose a very coarse 2-D mesh as the goal of our model is not to resolve the fine details of complex 2-D vortices that form around the junction, but to efficiently compute average water depth and velocity in the connected 1-D reaches. A special ghost cell technique is developed for coupling the reaches to the confluence region, which is one of the most important parts of a good 1-D/2-D coupling method. The proposed approach leads to very significant computational savings compared to numerically solving the full 2-D problem. We perform several numerical experiments to demonstrate plausibility of the proposed 1-D/2-D coupling model.