Skip to main content
SpringerLink
Log in

Virtual Element Method for an Elliptic Hemivariational Inequality with Applications to Contact Mechanics

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

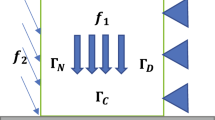
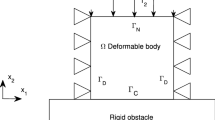
This paper is on the numerical solution of an elliptic hemivariational inequality by the virtual element method. We introduce an abstract framework of the numerical method and provide an error analysis. We then apply the virtual element method to solve two contact problems: a bilateral contact problem with friction and a frictionless normal compliance contact problem. Error estimates of their numerical solutions are derived, which are of optimal order for the linear virtual element method, under appropriate solution regularity assumptions. The discrete problem can be formulated as an optimization problem for a difference of two convex (DC) functions, and a convergent algorithm is introduced to solve it. Numerical examples are reported to show the performance of the proposed methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Ahmad, B., Alsaedi, A., Brezzi, F., Marini, L.D., Russo, A.: Equivalent projectors for virtual element methods. Comput. Math. Appl. 66(3), 376–391 (2013)

    Article  MathSciNet  Google Scholar 

  2. Artioli, E., Beirao Da Veiga, L., Lovadina, C., et al.: Arbitrary order 2D virtual elements for polygonal meshes: part I, elastic problem. Comput. Mech. 60(3), 355–377 (2017)

    Article  MathSciNet  Google Scholar 

  3. Barboteu, M., Bartosz, K., Han, W., Janiczko, T.: Numerical analysis of a hyperbolic hemivariational inequality arising in dynamic contact. SIAM J. Numer. Anal. 53(1), 527–550 (2015)

    Article  MathSciNet  Google Scholar 

  4. Barboteu, M., Bartosz, K., Kalita, P.: An analytical and numerical approach to a bilateral contact problem with nonmonotone friction. Int. J. Appl. Math. Comput. Sci. 23(2), 263–276 (2013)

    Article  MathSciNet  Google Scholar 

  5. Beirao Da Veiga, L., Brezzi, F., Cangiani, A., Manzini, G., et al.: Basic principles of virtual element methods. Math. Models Methods Appl. Sci. 23(1), 199–214 (2013)

    Article  MathSciNet  Google Scholar 

  6. Beirao Da Veiga, L., Brezzi, F., Marini, L.D.: Virtual elements for linear elasticity problems. SIAM J. Numer. Anal. 51(2), 794–812 (2013)

    Article  MathSciNet  Google Scholar 

  7. Beirao Da Veiga, L., Brezzi, F., Marini, L.D., Russo, A.: The Hitchhiker’s guide to the virtual element method. Math. Models Methods Appl. Sci. 24(8), 1541–1573 (2014)

    Article  MathSciNet  Google Scholar 

  8. Beirao Da Veiga, L., Lovadina, C., Russo, A.: Stability analysis for the virtual element method. Math. Models Methods Appl. Sci. 27(13), 2557–2594 (2017)

    Article  MathSciNet  Google Scholar 

  9. Brenner, S.C.: Korn’s inequalities for piecewise \(H^1\) vector fields. Math. Comput. 73(247), 1067–1087 (2004)

    Article  Google Scholar 

  10. Brenner, S.C., Guan, Q., Sung, L.: Some estimates for virtual element methods. Comput. Methods Appl. Math. 17(4), 553–574 (2017)

    Article  MathSciNet  Google Scholar 

  11. Brenner, S.C., Sung, L.: Virtual element methods on meshes with small edges or faces. Math. Models Methods Appl. Sci. 28(7), 1291–1336 (2018)

    Article  MathSciNet  Google Scholar 

  12. Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, 3rd edn. Springer, New York (2008)

    Book  Google Scholar 

  13. Brezzi, F., Buffa, A., Lipnikov, K.: Mimetic finite differences for elliptic problems. ESAIM: Math. Model. Numer. Anal. 43, 277–295 (2009)

    Article  MathSciNet  Google Scholar 

  14. Chen, L., Huang, J.: Some error analysis on virtual element methods. Calcolo 55(1), 5 (2018)

    Article  MathSciNet  Google Scholar 

  15. Clarke, F.H.: Optimization and Nonsmooth Analysis. Wiley, New York (1983)

    MATH  Google Scholar 

  16. Denkowski, Z., Migorski, S., Papageorgiou, N.S.: An Introduction to Nonlinear Analysis: Theory. Kluwer Academic Publishers, Boston (2003)

    Book  Google Scholar 

  17. Feng, F., Han, W., Huang, J.: Virtual element methods for elliptic variational inequalities of the second kind. J. Sci. Comput. 80, 60–80 (2019)

    Article  MathSciNet  Google Scholar 

  18. Han, W.: Numerical analysis of stationary variational–hemivariational inequalities with applications in contact mechanics. Math. Mech. Solids 23(3), 279–293 (2018)

    Article  MathSciNet  Google Scholar 

  19. Han, W., Migorski, S., Sofonea, M.: A class of variational-hemivariational inequalities with applications to frictional contact problems. SIAM J. Math. Anal. 46(6), 3891–3912 (2014)

    Article  MathSciNet  Google Scholar 

  20. Han, W., Sofonea, M., Barboteu, M.: Numerical analysis of elliptic hemivariational inequalities. SIAM J. Numer. Anal. 55(2), 640–663 (2017)

    Article  MathSciNet  Google Scholar 

  21. Han, W., Sofonea, M., Danan, D.: Numerical analysis of stationary variational-hemivariational inequalities. Numer. Math. 139, 563–592 (2018)

    Article  MathSciNet  Google Scholar 

  22. Haslinger, J., Miettinen, M., Panagiotopoulos, P.D.: Finite Element Method for Hemivariational Inequalities. Theory, Methods and Applications. Kluwer Academic, Dordrecht (1999)

    Book  Google Scholar 

  23. Joki, K., Bagirov, A.M., Karmitsa, N., et al.: Double bundle method for finding Clarke stationary points in nonsmooth DC programming. SIAM J. Optim. 28(2), 1892–1919 (2018)

    Article  MathSciNet  Google Scholar 

  24. Laursen, T.: Computational Contact and Impact Mechanics. Springer, New York (2002)

    MATH  Google Scholar 

  25. Migorski, S., Ochal, A., Sofonea, M.: Nonlinear Inclusions and Hemivariational Inequalities. Springer, New York (2013)

    Book  Google Scholar 

  26. Naniewicz, Z., Panagiotopoulos, P.D.: Mathematical Theory of Hemivariational Inequalities and Applications. Marcel Dekker, New York (1995)

    MATH  Google Scholar 

  27. Panagiotopoulos, P.D.: Hemivariational Inequalities, Applications in Mechanics and Engineering. Springer, Berlin (1993)

    Book  Google Scholar 

  28. Panagiotopoulos, P.D.: Nonconvex energy functions, hemivariational inequalities and substationarity principles. Acta Mech. 48(3–4), 111–130 (1983)

    Article  MathSciNet  Google Scholar 

  29. Sutton, O.J.: The virtual element method in 50 lines of MATLAB. Numer. Algorithms 75, 1141–1159 (2017)

    Article  MathSciNet  Google Scholar 

  30. Talischi, C., Paulino, G.H., Pereira, A., Menezes, I.F.M.: PolyMesher: a general-purpose mesh generator for polygonal elements written in Matlab. Struct. Multidiscip. Optim. 45(3), 309–328 (2012)

    Article  MathSciNet  Google Scholar 

  31. Wang, F., Wei, H.: Virtual element method for simplified friction problem. Appl. Math. Lett. 85, 125–131 (2018)

    Article  MathSciNet  Google Scholar 

  32. Wang, F., Wei, H.: Virtual element methods for the obstacle problem. IMA J. Numer. Anal. (2018). https://doi.org/10.1093/imanum/dry055

    Article  Google Scholar 

  33. Wriggers, P.: Computational Contact Mechanics, 2nd edn. Springer, Berlin (2006)

    Book  Google Scholar 

  34. Zeidler, E.: Nonlinear Functional Analysis and Its Applications. II/B: Nonlinear Monotone Operators. Springer, New York (1990)

    Book  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the referees for their valuable suggestions and comments on an early version of the paper.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, and MOE-LSC, Shanghai Jiao Tong University, Shanghai, 200240, China

    Fang Feng & Jianguo Huang

  2. Department of Mathematics, University of Iowa, Iowa City, IA, 52242, USA

    Weimin Han

Authors
  1. Fang Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weimin Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jianguo Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianguo Huang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The work of Weimin Han was partially supported by NSF under the Grant DMS-1521684.

The work of Jianguo Huang was partially supported by NSFC (Grant No. 11571237).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Feng, F., Han, W. & Huang, J. Virtual Element Method for an Elliptic Hemivariational Inequality with Applications to Contact Mechanics. J Sci Comput 81, 2388–2412 (2019). https://doi.org/10.1007/s10915-019-01090-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-019-01090-2

Keywords

Search

Navigation