Skip to main content
SpringerLink
Log in

Asymptotic Stability of Compact and Linear \(\theta \)-Methods for Space Fractional Delay Generalized Diffusion Equation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

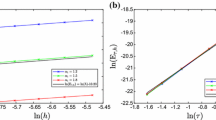
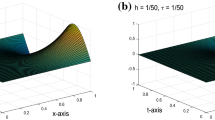
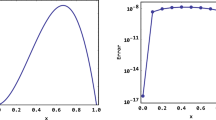
It is essential to explore the asymptotic stability of the numerical methods for fractional differential equations with delay since their exact solutions are unavailable or difficult to obtain. In this paper, we firstly derive a sufficient condition of the exact solution to be delay-independently asymptotically stable for the space fractional generalized diffusion equation with delay. Next, by applying the linear \(\theta \)-method to temporal dimension, we have established two classes of finite difference schemes independent of the delay for that, which have second-order and fourth-order accuracy in spatial dimension respectively. The unique solvability is proved and the local truncation error is derived. Furthermore, when \(\theta \in [0,1/2)\), we have obtained the necessary and sufficient condition of the asymptotic stability of both schemes under the specific conditions for the temporal step size \(\Delta t\) and the spatial step size h. When \(\theta \in [1/2,1]\), both schemes are unconditionally asymptotically stable. Moreover, the convergence results in the maximum norm are obtained according to the consistency analysis and the Lax theorem. The numerical examples are implemented to verify the theoretical results, which demonstrate that the asymptotic stabilities of both schemes are depending on the parameter \(\theta \) and the fractional derivative \(\alpha \), however, independent of the delay \(\tau \).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Aleksandrov, A.Y., Hu, G.D., Zhabko, A.P.: Delay-independent stability conditions for some classes of nonlinear systems. IEEE Trans. Autom. Control 59(8), 2209–2214 (2014)

    MathSciNet  MATH  Google Scholar 

  2. Andrei, D., Alexei, I.: Functional constraints method for constructing exact solutions to delay reaction-diffusion equations and more complex nonlinear equations. Commun. Nonlinear Sci. Numer. Simul. 19, 417–430 (2014)

    MathSciNet  Google Scholar 

  3. Axtell, M., Bise, M.E.: Factional calculus applications in control systems. In: Proceedings of the IEEE 1990 National Aerspace and Electronics Conferences, pp. 563–566 (1990)

  4. Barwell, V.K.: Special stability problems for functional differential equations. BIT Numer. Math. 15, 130–135 (1975)

    MathSciNet  MATH  Google Scholar 

  5. Bhalekar, S., Daftardar-Gejji, V.: A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calc. Appl. 1, 1–9 (2011)

    MATH  Google Scholar 

  6. Çelik, C., Duman, M.: Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. J. Comput. Phys. 231, 1743–1750 (2012)

    MathSciNet  MATH  Google Scholar 

  7. Cermák, J., Došláb, Z., Kisela, T.: Fractional differential equations with a constant delay: Stability and asymptotics of solutions. Appl. Math. Comput. 298, 336–350 (2017)

    MathSciNet  MATH  Google Scholar 

  8. Deng, W.H., Zhang, Z.J.: High Accuracy Algorithm for the Differential Equations Governing Anomalous Diffusion. World Scientific, Singapore (2019)

    MATH  Google Scholar 

  9. Duo, S.W., Zhang, Y.Z.: Numerical approximations for the tempered fractional Laplacian: error analysis and applications. J. Sci. Comput. 81(1), 569–593 (2019)

    MathSciNet  MATH  Google Scholar 

  10. García, P., Castro, M.A., Martín, J.A., Sirvent, A.: Convergence of two implicit numerical schemes for diffusion mathematical models with delay. Math. Comput. Model. 52, 1279–1287 (2010)

    MathSciNet  MATH  Google Scholar 

  11. Gatto, P., Hesthaven, J.S.: Numerical approximation of the fractional Laplacian via \(hp\)-finite elements, with an application to image denoising. J. Sci. Comput. 65, 249–270 (2015)

    MathSciNet  MATH  Google Scholar 

  12. Gao, C.B., Zhou, J.L., Zheng, X.Q., Lang, F.G.: Image enhancement based an improved fractional differentiation. J. Comput. Inf. Syst. 7, 257–264 (2011)

    Google Scholar 

  13. Gorenflo, R., Mainardi, F.: Random walk models for space-fractional diffusion processes. Frac. Calc. Appl. Anal. 1, 167–191 (1988)

    MathSciNet  MATH  Google Scholar 

  14. Grenander, U., Szegö, G.: Toeplitz Forms and Their Application, 2nd edn. AMS Chelsea, Providence (2001)

    MATH  Google Scholar 

  15. Guglielmi, N.: Delay dependent stability regions of \(\theta \)-methods for delay differential equations. IMA J. Numer. Anal. 18, 399–418 (1998)

    MathSciNet  MATH  Google Scholar 

  16. Guo, X., Li, Y., Wang, H.: A fourth-order scheme for space fractional diffusion equations. J. Comput. Phys. 373(15), 410–424 (2018)

    MathSciNet  MATH  Google Scholar 

  17. Hairer, E., Nösett, S.P., Wanner, G.: Solving Ordinary Differential Equations I, Nonstiff Problems. Springer, Berlin (1987)

    MATH  Google Scholar 

  18. Hao, Z.P., Cao, W.R.: An improved algorithm based on finite fifference schemes for fractional boundary value problems with nonsmooth solution. J. Sci. Comput. 73, 395–415 (2017)

    MathSciNet  MATH  Google Scholar 

  19. Hao, Z.P., Fan, K., Cao, W.R., Sun, Z.: A finite difference scheme for semilinear space-fractional diffusion equations with time delay. Appl. Math. Comput. 275, 238–254 (2016)

    MathSciNet  MATH  Google Scholar 

  20. Houwen, P.J., Sommeijer, B.P., Baker, C.T.H.: On the stability of predictor-corrector methods for parabolic equations with delay. IMA J. Numer. Anal. 6, 1–23 (1986)

    MathSciNet  MATH  Google Scholar 

  21. Huang, C., Vandewalle, S.: Unconditionally stable difference methods for delay partial differential equations. Numer. Math. 122(3), 579–601 (2012)

    MathSciNet  MATH  Google Scholar 

  22. Ilić, M., Liu, F., Turner, I., Anh, V.: Numerical approximation of a fractional-in-space diffusion equation, I. Fract. Calc. Appl. Anal. 9(4), 333–349 (2006)

    MathSciNet  MATH  Google Scholar 

  23. Jiang, X.Y., Xu, M.Y., Qi, H.T.: The fractional diffusion model with an absorption term and modified Fick’s law for non-local transport processes. Nonlinear Anal. Real World Appl. 11, 262–269 (2010)

    MathSciNet  MATH  Google Scholar 

  24. Jin, X.: Developments and Applications of Block Toeplitz Iterative Solvers. Science Press, Beijing (2002)

    Google Scholar 

  25. Kuang, J.X., Xiang, J., Tian, H.J.: The asymptotic stability of one-parameter methods for neutral differential equations. BIT Numer. Math. 34, 400–408 (1994)

    MathSciNet  MATH  Google Scholar 

  26. Lazarevic, M.P., Spasic, A.M.: Finite-time stability analysis of fractional order time-delay systems: Gronwall’s approach. Math. Comput. Model. 49, 475–481 (2009)

    MathSciNet  MATH  Google Scholar 

  27. Li, C.P., Zhang, F.R.: A survey on the stability of fractional differential equations. Eur. Phys. J. Spec. Top. 193, 27–47 (2011)

    Google Scholar 

  28. Liu, M., Spijker, M.N.: The stability of the \(\theta \)-methods in the numerical solution of delay differential equations. IMA J. Numer. Anal. 10, 1–48 (1990)

    MathSciNet  Google Scholar 

  29. Lubich, C.: Discretized fractional calculus. SIAM J. Math. Anal. 17, 704–719 (1986)

    MathSciNet  MATH  Google Scholar 

  30. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection-dispersion flow equations. J. Comput. Appl. Math. 172, 65–77 (2004)

    MathSciNet  MATH  Google Scholar 

  31. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 56, 80–90 (2006)

    MathSciNet  MATH  Google Scholar 

  32. Mishura, Y.: Fractional stochastic integration and Black-Scholes equation for fractional Brownian model with stochastic volatility. Stoch. Stoch. Rep. 76, 363–381 (2004)

    MathSciNet  MATH  Google Scholar 

  33. Mao, Z.P., Karniadakis, G.E.: A spectral method (of exponential convergence) for singular solutions of the diffusion equation with general two-sided fractional derivative. SIAM J. Numer. Anal. 56(1), 26–49 (2018)

    MathSciNet  MATH  Google Scholar 

  34. Mao, Z.P., Shen, J.: Efficient spectral-Galerkin methods for fractional partial differential equations with variable coefficients. J. Comput. Phys. 307, 243–261 (2016)

    MathSciNet  MATH  Google Scholar 

  35. Norkin, S.B., Elsgolts, L.E.: Introduction to the Theory and Application of Differential Equations with Deviating Arguments. Academic Press, New York (1973)

    Google Scholar 

  36. Ortigueira, M.D.: Riesz potential operators and inverses via fractional centred derivatives. Int. J. Math. Math. Sci. 2006, 1–12 (2006)

    MathSciNet  MATH  Google Scholar 

  37. Ortigueira, M.D., Machado, J.A.T.: Fractional signal processing and applications. Signal Process. 83, 2285–2286 (2003)

    Google Scholar 

  38. Podlubny, I.: Fractional-order systems and fractional-order controllers. Inst. Exp. Phys., Slovak Acad. Sci., UEF-03-94, Kosie (1994)

  39. Podlubny, I.: Fractional differential equations. In: Mathematics in Science and Engineering, vol. 198. Academic Press, San Diego, CA (1999)

  40. Reyes, E., Rodríguez, F., Martín, J.A.: Analytic-numerical solutions of diffusion mathematical models with delays. Comput. Math. Appl. 56, 743–753 (2008)

    MathSciNet  MATH  Google Scholar 

  41. Robert, M.G.: Toeplitz and circulant matrices: a review. Found. Trends Commun. Inf. Theory 2(3), 155–239 (2006)

    Google Scholar 

  42. Schumer, R., Benson, D.A., Meerschaert, M.M., Wheatcraft, S.W.: Eulerian derivation of the fractional advection-dispersion equation. J. Contam. Hydrol. 48(1), 69–88 (2001)

    Google Scholar 

  43. Si-Ammour, A., Djennoune, S., Bettayeb, M.: A sliding mode control for linear fractional systems with input and state delays. Commun. Nonlinear Sci. Numer. Simul. 14, 2310–2318 (2009)

    MathSciNet  MATH  Google Scholar 

  44. Sun, H., Sun, Z., Gao, G.: Some high order difference schemes for the space and time fractional Bloch-Torrey equations. Appl. Math. Comput. 281, 356–380 (2016)

    MathSciNet  MATH  Google Scholar 

  45. Tadjeran, C., Meerschaert, M.M., Scheffler, H.P.: A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys. 213, 205–213 (2006)

    MathSciNet  MATH  Google Scholar 

  46. Tian, H.: Asymptotic stability of numerical methods for linear delay parabolic differential equations. Comput. Math. Appl. 56, 1758–1765 (2008)

    MathSciNet  MATH  Google Scholar 

  47. Tian, H.: Asymptotic stability analysis of the linear \(\theta \)-method for linear parabolic differential equations with delay. J. Differ. Equ. Appl. 15(5), 473–487 (2009)

    MathSciNet  MATH  Google Scholar 

  48. Tian, W., Zhou, H., Deng, W.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84(294), 1703–1727 (2015)

    MathSciNet  MATH  Google Scholar 

  49. Thomas, J.W.: Numerical Partial Differential Equations: Finite Difference Methods. World Pub. Corp., New York (1995)

    MATH  Google Scholar 

  50. Tzou, D.Y.: The generalized lagging response in small-scale and high-rate heating. Int. J. Heat Mass. Trans. 38(17), 3231–3240 (1995)

    Google Scholar 

  51. Wang, H., Wang, K., Sircar, T.: A direct \(O(N\log ^2N)\) finite difference method for fractional diffusion equations. J. Comput. Phys. 229, 8095–8104 (2010)

    MathSciNet  MATH  Google Scholar 

  52. Wang, D., Zou, J.: Dissipativity and contractivity analysis for fractional functional differential equations and their numerical approximations. SIAM J. Numer. Anal. 57(3), 1445–1470 (2019)

    MathSciNet  MATH  Google Scholar 

  53. Wang, J., Liang, J.R., Lv, L.J., Qiu, W.Y., Ren, F.Y.: Continuous time Black-Scholes equation with transaction costs in subdiffusive fractional Brownian motion regime. Phys. A 391, 750–759 (2012)

    MathSciNet  Google Scholar 

  54. Wang, W., Rao, T., Shen, W., Zhong, P.: A posteriori error analysis for Crank-Nicolson-Galerkin type methods for reaction-diffusion equations with delay. SIAM J. Sci. Comput. 40(2), A1095–A1120 (2018)

    MathSciNet  MATH  Google Scholar 

  55. Wang, W., Zhang, C.: Preserving stability implicit Euler method for nonlinear Volterra and neutral functional differential equations in Banach space. Numer. Math. 115(3), 451–474 (2010)

    MathSciNet  MATH  Google Scholar 

  56. Wu, F., Li, D., Wen, J., Duan, J.: Stability and convergence of compact finite difference method for parabolic problems with delay. Appl. Math. Comput. 322, 129–139 (2018)

    MathSciNet  MATH  Google Scholar 

  57. Yan, Y., Kou, C.: Stability analysis of a fractional differential model of HIV infection of CD4\(^+\) T-cells with time delay. Math. Comput. Simul. 82, 1572–1585 (2012)

    MathSciNet  MATH  Google Scholar 

  58. Yan, Y., Sun, Z.Z., Zhang, J.: Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations: a second-order scheme. Commun. Comput. Phys. 22, 1028–1048 (2017)

    MathSciNet  Google Scholar 

  59. Yang, Q., Liu, F., Turner, I.: Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 34, 200–218 (2010)

    MathSciNet  MATH  Google Scholar 

  60. Zayernouri, M., Cao, W., Zhang, Z., Karniadakis, G.E.: Spectral and discontinuous spectral element methods for fractional delay equation. SIAM J. Sci. Comput. 36(6), B904–B929 (2014)

    MathSciNet  MATH  Google Scholar 

  61. Zhang, Q., Zhang, C., Wang, L.: The compact and Crank-Nicolson ADI schemes for two-dimensional semilinear multidelay parabolic equations. J. Comput. Appl. Math. 306, 217–230 (2016)

    MathSciNet  MATH  Google Scholar 

  62. Zhang, Q., Chen, M., Xu, Y., Xu, D.: Compact \(\theta \)-method for the generalized delay diffusion equation. Appl. Math. Comput. 316(1), 357–369 (2018)

    MathSciNet  MATH  Google Scholar 

  63. Zhang, Q., Ran, M., Xu, D.: Analysis of the compact difference scheme for the semilinear fractional partial differential equation with time delay. Appl. Anal. 96(11), 1867–1884 (2017)

    MathSciNet  MATH  Google Scholar 

  64. Zhang, Q., Ren, Y., Lin, X., Xu, Y.: Uniform convergence of compact and BDF methods for the space fractional semilinear delay reaction–diffusion equations. Appl. Math. Comput. 358, 91–110 (2019)

    MathSciNet  Google Scholar 

  65. Zhao, J.J., Fan, Y., Xu, Y.: Stability of symmetric Runge–Kutta methods for neutral delay integro-differential equations. SIAM J. Numer. Anal. 55(1), 328–348 (2017)

    MathSciNet  MATH  Google Scholar 

  66. Zhao, L.J., Deng, W.H., Hesthaven J.S.: Characterization of image spaces of Riemann–Liouville fractional integral operators on Sobolev spaces. arXiv:1603.06511v2 [math.NA]

  67. Zhao, X., Sun, Z., Peng, H.: A fourth-order compact ADI scheme for 2D nonlinear space fractional Schrödinger equation. SIAM J. Sci. Comput. 36(6), A2865–A2886 (2014)

    MATH  Google Scholar 

  68. Zhao, Y., Zhu, P., Luo, W.: A fast second-order implicit scheme for non-linear time-space fractional diffusion equation with time delay and drift term. Appl. Math. Comput. 336, 231–248 (2018)

    MathSciNet  MATH  Google Scholar 

  69. Zhou, H., Tian, W., Deng, W.: Quasi-compact finite difference schemes for space fractional diffusion equations. J. Sci. Comput. 56, 45–66 (2013)

    MathSciNet  MATH  Google Scholar 

  70. Zhou, P.: On the unity of circle and straight line on the complex plane. J. Chizhou Teach. Coll. 18, 64–65 (2004). (in Chinese)

    Google Scholar 

  71. Zubik-Kowal, B.: Stability in the numerical solution of linear parabolic equations with a delay term. BIT Numer. Math. 41, 191–206 (2001)

    MathSciNet  MATH  Google Scholar 

  72. Zubik-Kowal, B.: The method of lines for parabolic differential-functional equations. IMA J. Numer. Anal. 17, 103–123 (1997)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the editor and the anonymous reviewers for their careful reading and many patient checking of the whole manuscript. Their valuable suggestions and comments significantly improve the quality of the manuscript.

Funding

This work was supported by Natural Science Foundation of China (Grant No. 11501514), Natural Science Foundation of Zhejiang Province (Grant No. LY19A010026), Zhejiang Province “Yucai” Project (Grant No. 2019YCGC012), Visiting Scholar Program of China Scholarship Council (Grant No. 201908330528), and Fundamental Research Funds of Zhejiang Sci-Tech University (Grant No. 2019Q072).

Author information

Authors and Affiliations

  1. Department of Mathematics, Zhejiang Sci-Tech University, Hangzhou, 310018, China

    Qifeng Zhang & Tingyue Li

  2. Department of Mathematics, Southeast University, Nanjing, 210096, China

    Qifeng Zhang

  3. School of Mathematics, Shanghai University of Finance and Economics, Shanghai, 200433, China

    Tingyue Li

Authors
  1. Qifeng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tingyue Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qifeng Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Q., Li, T. Asymptotic Stability of Compact and Linear \(\theta \)-Methods for Space Fractional Delay Generalized Diffusion Equation. J Sci Comput 81, 2413–2446 (2019). https://doi.org/10.1007/s10915-019-01091-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-019-01091-1

Keywords

Search

Navigation