Skip to main content
SpringerLink
Log in

Coupling FEM with a Multiple-Subdomain Trefftz Method

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

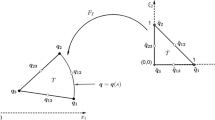
We consider 2D electromagnetic scattering at bounded objects consisting of different, possibly inhomogeneous materials. We propose and compare three approaches to couple the finite element method (FEM) in a meshed domain encompassing material inhomogeneities and the multiple multipole program (MMP) in the unbounded complement. MMP is a Trefftz method, as it employs trial spaces composed of exact solutions of the homogeneous problem. Each of these global basis functions is anchored at a point that, if singular, is placed outside the respective domain of approximation. In the MMP domain we assume that material parameters are piecewise constant, which induces a partition: one unbounded subdomain and other bounded, but possibly very large, subdomains, each requiring its own Trefftz trial space. Coupling approaches arise from seeking stationary points of Lagrangian functionals that both enforce the variational form of the equations in the FEM domain and match the different trial functions across subdomain interfaces. Hence, on top of the transmission conditions connecting the FEM and MMP domains, one also has to impose transmission conditions between the MMP subdomains. Specifically, we consider the following coupling approaches:

  1. 1.

    Least-squares-based coupling using techniques from PDE-constrained optimization.

  2. 2.

    Multi-field variational formulation in the spirit of mortar finite element methods.

  3. 3.

    Discontinuous Galerkin coupling between the meshed FEM domain and the single-entity MMP subdomains.

We compare these approaches in a series of numerical experiments with different geometries and material parameters, including examples that exhibit triple-point singularities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Notes

  1. The subscript “loc” indicates that functions belong to the reported space after multiplication with a compactly-supported smooth function.

Abbreviations

MMP::

Multiple multipole program

FEM::

Finite element method

TPS::

Triple-point singularity

PDE::

Partial differential equation

DoF::

Degree of freedom

DG::

Discontinuous Galerkin

BEM::

Boundary element method

Subscript \(\text {f}\) in formulas::

FEM

Subscript \(\text {m}\) in formulas::

MMP

Superscript n in formulas::

Discrete

References

  1. Antunes, P.R.S.: A numerical algorithm to reduce ill-conditioning in meshless methods for the Helmholtz equation. Numer. Algorithms 79(3), 879–897 (2018). https://doi.org/10.1007/s11075-017-0465-z

    Article  MathSciNet  MATH  Google Scholar 

  2. Arnold, D.N., Brezzi, F., Cockburn, B., Marini, L.D.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39(5), 1749–1779 (2002). https://doi.org/10.1137/S0036142901384162

    Article  MathSciNet  MATH  Google Scholar 

  3. Babuška, I.M., Sauter, S.A.: Is the pollution effect of the FEM avoidable for the Helmholtz equation considering high wave numbers? SIAM Rev. 42(3), 451–484 (2000). https://doi.org/10.2307/2653302

    Article  MathSciNet  MATH  Google Scholar 

  4. Barnett, A.H., Betcke, T.: An exponentially convergent nonpolynomial finite element method for time-harmonic scattering from polygons. SIAM J. Sci. Comput. 32(3), 1417–1441 (2010). https://doi.org/10.1137/090768667

    Article  MathSciNet  MATH  Google Scholar 

  5. Bohren, C.F., Huffman, D.R.: Absorption and Scattering of Light by Small Particles. Wiley, New York (2007). https://doi.org/10.1002/9783527618156

    Book  Google Scholar 

  6. Brezzi, F., Marini, L.D.: A three-field domain decomposition method. In: Domain decomposition methods in science and engineering (Como, 1992), Contemp. Math., vol. 157, pp. 27–34. Amer. Math. Soc., Providence, RI (1994). https://doi.org/10.1090/conm/157/01402

  7. Casagrande, R.: Discontinuous finite element methods for eddy current simulation. Ph.D. Thesis, Seminar for Applied Mathematics, ETH Zurich, Switzerland (2017). https://doi.org/10.3929/ethz-a-010863105

  8. Casati, D., Codecasa, L., Hiptmair, R., Moro, F.: Trefftz co-chain calculus. Technical Report 2019-19, Seminar for Applied Mathematics, ETH Zurich, Switzerland (2019). https://www.sam.math.ethz.ch/sam_reports/reports_final/reports2019/2019-19.pdf

  9. Casati, D., Hiptmair, R.: Coupling finite elements and auxiliary sources. Comput. Math. Appl. 77(6), 1513–1526 (2019). https://doi.org/10.1016/j.camwa.2018.09.007

    Article  MathSciNet  Google Scholar 

  10. Casati, D., Hiptmair, R., Smajic, J.: Coupling finite elements and auxiliary sources for Maxwell’s equations. Int. J. Numer. Model. Electron. Netw. Dev. Fields (2018). https://doi.org/10.1002/jnm.2534

    Article  Google Scholar 

  11. Casati, D., Hiptmair, R., Smajic, J.: Coupling finite elements and auxiliary sources for electromagnetic wave propagation. Technical Report 2019-62, Seminar for Applied Mathematics, ETH Zurich, Switzerland (2019). https://www.sam.math.ethz.ch/sam_reports/reports_final/reports2019/2019-62.pdf

  12. Casati, D., Smajic, J., Hiptmair, R.: \(\mathbf{H}\)-\(\phi \) field formulation with lumped sources and unbounded domains. IEEE Trans. Magn. 56(1), 1–4 (2020). https://doi.org/10.1109/TMAG.2019.2949625

    Article  Google Scholar 

  13. Colton, D., Kress, R.: Inverse Acoustic and Electromagnetic Scattering Theory. Applied Mathematical Sciences, vol. 93, 3rd edn. Springer, Heidelberg (2013)

    Book  Google Scholar 

  14. Dijkstra, W.: Condition numbers in the boundary element method: shape and solvability. Ph.D. Thesis, Department of Mathematics and Computer Science, Technische Universiteit Eindhoven, Netherlands (2008). https://doi.org/10.6100/IR633956

  15. Gerdes, K.: A summary of infinite element formulations for exterior Helmholtz problems. Comput. Methods Appl. Mech. Eng. 164(1), 95–105 (1998). https://doi.org/10.1016/S0045-7825(98)00048-6

    Article  MathSciNet  MATH  Google Scholar 

  16. Geuzaine, C., Remacle, J.F., et al.: Gmsh v4.4.1. http://gmsh.info (2019). Accessed 25 July 2019

  17. Graham, I.G., Pembery, O.R., Spence, E.A.: The Helmholtz equation in heterogeneous media: a priori bounds, well-posedness, and resonances. J. Differ. Equ. 266(6), 2869–2923 (2019). https://doi.org/10.1016/j.jde.2018.08.048

    Article  MathSciNet  MATH  Google Scholar 

  18. Greengard, L., Lee, J.Y.: Stable and accurate integral equation methods for scattering problems with multiple material interfaces in two dimensions. J. Comput. Phys. 231, 2389–2395 (2012). https://doi.org/10.1016/j.jcp.2011.11.034

    Article  MathSciNet  MATH  Google Scholar 

  19. Guennebaud, G., Jacob, B., et al.: Eigen v3.3.7. http://eigen.tuxfamily.org (2018). Accessed 11 Dec 2018

  20. Gyimesi, M., Tsukerman, I., Lavers, D., Pawlak, T., Ostergaard, D.: Hybrid finite element-trefftz method for open boundary analysis. IEEE Trans. Magn. 32(3), 671–674 (1996). https://doi.org/10.1109/20.497327

    Article  Google Scholar 

  21. Hafner, C.: Beiträge zur Berechnung der Ausbreitung elektromagnetischer Wellen in zylindrischen Strukturen mit Hilfe des “Point-Matching”-Verfahrens (1980)

  22. Heifetz, A., Kong, S.C., Sahakian, A.V., Taflove, A., Backman, V.: Photonic nanojets. J. Comput. Theoret. Nanosci. 6(9), 1979–1992 (2009). https://doi.org/10.1166/jctn.2009.1254

    Article  Google Scholar 

  23. Hiptmair, R., Moiola, A., Perugia, I.: A survey of Trefftz methods for the Helmholtz equation, pp. 237–279. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41640-3_8

    Book  MATH  Google Scholar 

  24. Jackson, J.D.: Classical electrodynamics, 3rd edn. Wiley, New York (1999)

    MATH  Google Scholar 

  25. McLean, W.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  26. Mie, G.: Elektrische Wellen an zwei parallelen Drähten. Ann. Phys. 307, 201–249 (1900). https://doi.org/10.1002/andp.19003070602

    Article  MATH  Google Scholar 

  27. Moiola, A.: Trefftz-discontinuous Galerkin methods for time-harmonic wave problems. Ph.D. Thesis, Seminar for Applied Mathematics, ETH Zurich, Switzerland (2011). https://doi.org/10.3929/ethz-a-006698757

  28. Monk, P.: Finite element methods for Maxwell’s equations. Clarendon Press, Oxford (2003). https://doi.org/10.1093/acprof:oso/9780198508885.001.0001

    Book  MATH  Google Scholar 

  29. Murakami, H., Shioya, S., Yamada, R., Luco, J.E.: Transmitting boundaries for time-harmonic elastodynamics on infinite domains. Int. J. Numer. Methods Eng. 17(11), 1697–1716 (1981). https://doi.org/10.1002/nme.1620171109

    Article  MATH  Google Scholar 

  30. Popp, A., Wohlmuth, B.I., Gee, M.W., Wall, W.A.: Dual quadratic mortar finite element methods for 3D finite deformation contact. SIAM J. Sci. Comput. 34(4), B421–B446 (2012). https://doi.org/10.1137/110848190

    Article  MathSciNet  MATH  Google Scholar 

  31. Sauter, S.A., Schwab, C.: Boundary Element Methods. Springer Series in Computational, vol. 39. Springer, Berlin (2011). https://doi.org/10.1007/978-3-540-68093-2

    Book  MATH  Google Scholar 

  32. Schenk, O., et al.: PARDISO v6.0. https://www.pardiso-project.org (2018). Accessed May 2018

  33. Smajic, J., Hafner, C., Leuthold, J.: Coupled FEM–MMP for computational electromagnetics. IEEE Trans. Magn. 52(3), 1–4 (2015). https://doi.org/10.1109/TMAG.2015.2475241

    Article  Google Scholar 

  34. Stenberg, R.: Mortaring by a method of J.A. Nitsche. In: Idelsohn, S., Oñate, E., Dvorkin, E. (eds.) Computational Mechanics-New Trends and Applications. CIMNE, Barcelona (1998)

    Google Scholar 

  35. Süli, E., Schwab, C., Houston, P.: hp-DGFEM for partial differential equations with nonnegative characteristic form. In: Cockburn, B., Karniadakis, G.E., Shu, C.W. (eds.) Discontinuous Galerkin methods. Lecture Notes in Computational Science and Engineering, vol. 11, pp. 221–230. Springer, Berlin (2000)

    Chapter  Google Scholar 

  36. Tonti, E.: A direct discrete formulation of field laws: the cell method. CMES—Comput. Model. Eng. Sci. 2(2), 237–258 (2001)

    Google Scholar 

  37. Vekua, I.N.: New Methods for Solving Elliptic Equations. North Holland Publishing Company, Amsterdam (1967)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Seminar for Applied Mathematics, ETH Zurich, Rämistrasse 101, 8092, Zurich, Switzerland

    Daniele Casati & Ralf Hiptmair

Authors
  1. Daniele Casati
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ralf Hiptmair
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daniele Casati.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by the Swiss National Science Foundation [Grant No. 2000021_165674/1].

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Casati, D., Hiptmair, R. Coupling FEM with a Multiple-Subdomain Trefftz Method. J Sci Comput 82, 74 (2020). https://doi.org/10.1007/s10915-020-01179-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01179-z

Keywords

Mathematics Subject Classification

Search

Navigation