Local Discontinuous Galerkin Methods to a Dispersive System of KdV-Type Equations

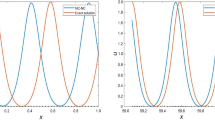
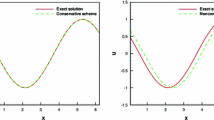
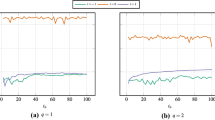
Abstract

In this paper, we develop and analyze a series of conservative and dissipative local discontinuous Galerkin (LDG) methods for the dispersive system of Korteweg–de Vries (KdV) type equations. Based on a cardinal conservative quantity of this system, we design and discuss two different types of numerical fluxes, including the conservative and dissipative ones for the linear and nonlinear terms respectively. Thus, one conservative together with three dissipative LDG schemes for the KdV-type system are developed in our paper. The invariant preserving property for the conservative scheme and corresponding dissipative properties for the other three dissipative schemes are all presented and proven in this paper. The error estimates for two schemes are given, whose numerical fluxes for linear terms are chosen as the dissipative type. Assuming that the discontinuous piecewise polynomials of degree less than or equal to k are adopted, and conservative numerical fluxes are employed to discretize the nonlinear terms, we obtain a suboptimal a priori bound of order k; yet in the case of dissipative fluxes, we obtain a slightly better bound of order $k+\frac{1}{2}$. Numerical experiments for this system in different circumstances are provided, including accuracy tests for two kinds of traveling waves, long-time simulations for solitary waves and interactions of multi-solitary waves, to illustrate the accuracy and capability of these schemes.

Appendices

Appendices

Proof of Lemma 4.4

Proof

We separate the following proof into two parts according to the conservative and dissipative cases for ${\mathcal {I}}$.

• (The conservative case for ${\mathcal {I}}_c$)

  $$\begin{aligned}&{\mathcal {I}}_c(u_h,v_h) \nonumber \\&\quad = (2aA{\mathcal {N}}_c(u_h,u_h;u_h) + bD{\mathcal {N}}_c(u_h,u_h;u_h) + bC{\mathcal {N}}_c(v_h,v_h;v_h) + 2cF{\mathcal {N}}_c(v_h,v_h;v_h)) \nonumber \\&\qquad + (bA{\mathcal {N}}_c(u_h,u_h;v_h) + 2cD{\mathcal {N}}_c(u_h,u_h;v_h) + 2aB{\mathcal {N}}_c(u_h,v_h;u_h) + bE{\mathcal {N}}_c(u_h,v_h;u_h)) \nonumber \\&\qquad + (2aC{\mathcal {N}}_c(v_h,v_h;u_h) + bF{\mathcal {N}}_c(v_h,v_h;u_h) + bB{\mathcal {N}}_c(u_h,v_h;v_h) + 2cE{\mathcal {N}}_c(u_h,v_h;v_h)) \nonumber \\&\quad :=({\mathcal {I}}_{c,1}) + ({\mathcal {I}}_{c,2}) + ({\mathcal {I}}_{c,3}). \end{aligned}$$

  (A.1)

  With the conservative property ${\mathcal {N}}_c(u,u;u)=0$ given in (2.16), the first term $({\mathcal {I}}_{c,1})=0$. By virtue of relations (2.14) and (2.15), and the conditions in (1.4), i.e.

  $$\begin{aligned}&2Ba + (E-2A)b - 4Dc = 0,\\&4Ca + (2F-B)b - 2Ec = 0, \end{aligned}$$

  the left two terms, $({\mathcal {I}}_{c,2})$ and $({\mathcal {I}}_{c,3})$, satisfy

  $$\begin{aligned}&({\mathcal {I}}_{c,2}) = \frac{1}{2}(2bA+4cD-2aB-bE){\mathcal {N}}_c(u_h,u_h;v_h) = 0, \\&({\mathcal {I}}_{c,3}) = \frac{1}{2}(4aC+2bF-bB-2cE){\mathcal {N}}_c(v_h,v_h;u_h) = 0. \end{aligned}$$

• (The dissipative case for ${\mathcal {I}}_d$)

  $$\begin{aligned}&{\mathcal {I}}_d(u_h,v_h) \nonumber \\&\quad = (2aA{\mathcal {N}}_d(u_h,u_h;u_h) + bD{\mathcal {N}}_d(u_h,u_h;u_h) + bC{\mathcal {N}}_d(v_h,v_h;v_h) + 2cF{\mathcal {N}}_d(v_h,v_h;v_h)) \nonumber \\&\qquad + (bA{\mathcal {N}}_d(u_h,u_h;v_h) + 2cD{\mathcal {N}}_d(u_h,u_h;v_h) + 2aB{\mathcal {N}}_d(u_h,v_h;u_h) + bE{\mathcal {N}}_d(u_h,v_h;u_h)) \nonumber \\&\qquad + (2aC{\mathcal {N}}_d(v_h,v_h;u_h) + bF{\mathcal {N}}_d(v_h,v_h;u_h) + bB{\mathcal {N}}_d(u_h,v_h;v_h) + 2cE{\mathcal {N}}_d(u_h,v_h;v_h)) \nonumber \\&\qquad + \frac{\varepsilon }{2} \sum _{j=1}^{N}\left( {2a[u_h]^2+2b[u_h][v_h]+2c[v_h]^2}\right) _{j-\frac{1}{2}} \nonumber \\&\quad :=({\mathcal {I}}_{d,1}) + ({\mathcal {I}}_{d,2}) + ({\mathcal {I}}_{d,3}) + ({\mathcal {I}}_{d,4}). \end{aligned}$$

  (A.2)

  Applying the properties of ${\mathcal {N}}_d$ in (2.25) and (2.26) and the conditions of a, b, c in (1.4),

  $$\begin{aligned}&2Ba + (E-2A)b - 4Dc = 0,\\&4Ca + (2F-B)b - 2Ec = 0, \end{aligned}$$

  hence $({\mathcal {I}}_{d1})$, $({\mathcal {I}}_{d2})$ and $({\mathcal {I}}_{d3})$ become

  $$\begin{aligned} ({\mathcal {I}}_{d,1})&= -\frac{1}{6}(2aA+bD)\sum _{j=1}^{N}\left( {[u]^2[u]}\right) _{j-\frac{1}{2}} - \frac{1}{6}(bC+2cF)\sum _{j=1}^{N}\left( {[v]^2[v]}\right) _{j-\frac{1}{2}} \nonumber \\&\ge -\frac{1}{3}(2aA+bD)\Vert u\Vert _{\infty } \sum _{j=1}^{N}\left( {[u]^2}\right) _{j-\frac{1}{2}} - \frac{1}{3}(bC+2cF)\Vert v\Vert _{\infty }\sum _{j=1}^{N}\left( {[v]^2}\right) _{j-\frac{1}{2}}, \end{aligned}$$

  (A.3)
  $$\begin{aligned} ({\mathcal {I}}_{d,2})&= -\frac{1}{2}(2cD + bA)\sum _{j=1}^{N}\left( {[u]^2[v]}\right) _{j-\frac{1}{2}} \ge - (2cD + bA) \Vert v\Vert _{\infty }\sum _{j=1}^{N}\left( {[u]^2}\right) _{j-\frac{1}{2}}, \end{aligned}$$

  (A.4)

  and

  $$\begin{aligned} ({\mathcal {I}}_{d,3}) = -\frac{1}{2}(2aC + bF)\sum _{j=1}^{N}\left( {[v]^2[u]}\right) _{j-\frac{1}{2}} \ge - (2aC + bF)\Vert u\Vert _{\infty }\sum _{j=1}^{N}\left( {[v]^2}\right) _{j-\frac{1}{2}}. \end{aligned}$$

  (A.5)

  Combining the above three inequalities together, we have

  $$\begin{aligned}&({\mathcal {I}}_{d,1})+({\mathcal {I}}_{d,2})+({\mathcal {I}}_{d,3})\nonumber \\&\quad \ge -\left( \frac{1}{3}(2aA+bD)\Vert u\Vert _{\infty } + (2cD + bA) \Vert v\Vert _{\infty } \right) \sum _{j=1}^{N}\left( {[u]^2}\right) _{j-\frac{1}{2}} \nonumber \\&\qquad - \left( \frac{1}{3}(bC+2cF)\Vert v\Vert _{\infty } + (2aC + bF)\Vert u\Vert _{\infty } \right) \sum _{j=1}^{N}\left( {[v]^2}\right) _{j-\frac{1}{2}} \nonumber \\&\quad = -\varLambda _1 \sum _{j=1}^{N}\left( {[u]^2}\right) _{j-\frac{1}{2}} - \varLambda _2 \sum _{j=1}^{N}\left( {[v]^2}\right) _{j-\frac{1}{2}}. \end{aligned}$$

  (A.6)

  Now we take into consideration of $({\mathcal {I}}_4)$ with the positive definite condition (1.5) which means there is a positive number $\alpha$ such that $\alpha (\xi ^2+\zeta ^2)\le a\xi ^2 + b\xi \zeta + c\zeta ^2$, in detail

  $$\begin{aligned} ({\mathcal {I}}_{d,4}) = \varepsilon \sum _{j=1}^{N}\left( {a[u]^2+b[u][v]+c[v]^2}\right) _{j-\frac{1}{2}} \ge \varepsilon \alpha \sum _{j=1}^{N}\left( {[u]^2 + [v]^2}\right) _{j-\frac{1}{2}}. \end{aligned}$$

  (A.7)

  Comparing (A.6) with (A.7), applying the additional conditions for the parameter $\varepsilon$ that

  $$\begin{aligned} \varepsilon \ge \frac{1}{\alpha }\max \left( |\varLambda _1|, |\varLambda _2|\right) , \end{aligned}$$

  (A.8)

  then we obtain the following inequality

  $$\begin{aligned} {\mathcal {I}}_d(u_h,v_h) \ge -\varLambda _1 \sum _{j=1}^{N}\left( {[u]^2}\right) _{j-\frac{1}{2}} - \varLambda _2 \sum _{j=1}^{N}\left( {[v]^2}\right) _{j-\frac{1}{2}} + \varepsilon \alpha \sum _{j=1}^{N}\left( {[u]^2 + [v]^2}\right) _{j-\frac{1}{2}} \ge 0. \end{aligned}$$

$\square$

Proof of Lemma 4.5

Proof

We separate the following proofs into two parts according to the conservative and dissipative cases for ${\mathcal {J}}$.

• (The conservative case for ${\mathcal {J}}_c$). Take account of the Eqs. (3.4), (3.5) by choosing the test functions as follows

  $$\begin{aligned} \xi _1=q^{(u)}_h,\quad \zeta _1=-p^{(u)}_h. \end{aligned}$$

  (B.1)

  Combine (3.4) and (3.5) together, sum up over j and take into consideration of the periodic condition, then we have

  $$\begin{aligned}&\sum _{j=1}^{N}\left( {p^{(u)}_h,q^{(u)}_h}\right) _{I_j} + \sum _{j=1}^{N}\left( {q^{(u)}_h,(q^{(u)}_h)_x}\right) _{I_j} + \sum _{j=1}^{N}\left( {{\widehat{q}}^{(u)}_h[q^{(u)}_h]}\right) _{j-\frac{1}{2}} \nonumber \\&\quad + \sum _{j=1}^{N}\left( {q^{(u)}_h,-p^{(u)}_h}\right) _{I_j} + \sum _{j=1}^{N}\left( {u_h,(-p^{(u)}_h)_x}\right) _{I_j} + \sum _{j=1}^{N}\left( {{\widehat{u}}_h[-p^{(u)}_h]}\right) _{j-\frac{1}{2}} = 0. \end{aligned}$$

  (B.2)

  Noticing that the first term can eliminate the forth term, and recalling the choice of the numerical flux ${\widehat{q}}^{(u)}_h=\{q^{(u)}_h\}$ with the property ${\mathcal {D}}^{\star }(q^{(u)}_h, q^{(u)}_h)=0$ in (2.34), namely

  $$\begin{aligned} \sum _{j=1}^{N}\left( \left( {q^{(u)}_h,(q^{(u)}_h)_x}\right) _{I_j} +\left( {\{q^{(u)}_h\}[q^{(u)}_h]}\right) _{j-\frac{1}{2}}\right) =0, \end{aligned}$$

  (B.3)

  then we can simplify the Eq. (B.2) into

  $$\begin{aligned} {\mathcal {D}}^{\star }(u_h,p^{(u)}_h)=-\sum _{j=1}^{N}\left( {u_h,(p^{(u)}_h)_x}\right) _{I_j} - \sum _{j=1}^{N}\left( {\{u_h\} [p^{(u)}_h]}\right) _{j-\frac{1}{2}} = 0. \end{aligned}$$

  (B.4)

  Herein we use the form ${\mathcal {D}}^{\star }$ defined in (2.29) introduced for the reason of concision. The same procedure can also be applied in (3.7) and (3.8) with taking test functions as

  $$\begin{aligned} \xi _2=q^{(v)}_h,\quad \zeta _2=-p^{(v)}_h, \end{aligned}$$

  (B.5)

  then we get

  $$\begin{aligned} {\mathcal {D}}^{\star }(v_h,p^{(v)}_h)=-\sum _{j=1}^{N}\left( {v_h,(p^{(v)}_h)_x}\right) _{I_j} - \sum _{j=1}^{N}\left( {\{v_h\}[p^{(v)}_h]}\right) _{j-\frac{1}{2}} = 0. \end{aligned}$$

  (B.6)

  Next we retake the test functions in (3.4), (3.5), (3.7) and (3.8) as

  $$\begin{aligned} \xi _1=q^{(v)}_h,\quad \zeta _1=-p^{(v)}_h,\quad \xi _2=q^{(u)}_h,\quad \zeta _2=-p^{(u)}_h, \end{aligned}$$

  (B.7)

  then combine four equations together

  $$\begin{aligned}&\sum _{j=1}^{N}\left( {p^{(u)}_h,q^{(v)}_h}\right) _{I_j} + \sum _{j=1}^{N}\left( {q^{(u)}_h,-p^{(v)}_h}\right) _{I_j} + \sum _{j=1}^{N}\left( {p^{(v)}_h,q^{(u)}_h}\right) _{I_j} + \sum _{j=1}^{N}\left( {q^{(v)}_h,-p^{(u)}_h}\right) _{I_j} \nonumber \\&\quad + \sum _{j=1}^{N}\left( {q^{(u)}_h,(q^{(v)}_h)_x}\right) _{I_j} + \sum _{j=1}^{N}\left( {q^{(v)}_h,(q^{(u)}_h)_x}\right) _{I_j}\nonumber \\&\quad + \sum _{j=1}^{N}\left( {{\widehat{q}}^{(u)}_h[q^{(v)}_h]}\right) _{j-\frac{1}{2}} + \sum _{j=1}^{N}\left( {{\widehat{q}}^{(v)}_h[q^{(u)}_h]}\right) _{j-\frac{1}{2}} \nonumber \\&\quad - \sum _{j=1}^{N}\left( {u_h,(p^{(v)}_h)_x}\right) _{I_j} - \sum _{j=1}^{N}\left( {{\widehat{u}}_h[p^{(v)}_h]}\right) _{j-\frac{1}{2}} - \sum _{j=1}^{N}\left( {v_h,(p^{(u)}_h)_x}\right) _{I_j} \nonumber \\&\quad - \sum _{j=1}^{N}\left( {{\widehat{v}}_h[p^{(u)}_h]}\right) _{j-\frac{1}{2}} = 0. \end{aligned}$$

  (B.8)

  Obviously, the first four terms cancel out immediately. With definitions of ${\widehat{q}}^{(u)}_h$ and ${\widehat{q}}^{(v)}_h$ and the equality ${\mathcal {D}}^{\star }(q^{(u)}_h,q^{(v)}_h) + {\mathcal {D}}^{\star }(q^{(v)}_h, q^{(u)}_h)=0$, the second four terms also vanish, i.e.

  $$\begin{aligned}&\sum _{j=1}^{N}\left( {q^{(u)}_h,(q^{(v)}_h)_x}\right) _{I_j} + \sum _{j=1}^{N}\left( {{\widehat{q}}^{(u)}_h[q^{(v)}_h]}\right) _{j-\frac{1}{2}} \nonumber \\&\quad + \sum _{j=1}^{N}\left( {q^{(v)}_h,(q^{(u)}_h)_x}\right) _{I_j} + \sum _{j=1}^{N}\left( {{\widehat{q}}^{(v)}_h[q^{(u)}_h]}\right) _{j-\frac{1}{2}} =0. \end{aligned}$$

  (B.9)

  Thus it leads to another identity

  $$\begin{aligned}&{\mathcal {D}}^{\star }(u_h,p^{(v)}_h)+{\mathcal {D}}^{\star }(v_h,p^{(u)}_h) \nonumber \\&\quad = -\sum _{j=1}^{N}\left( {u_h,(p^{(v)}_h)_x}\right) _{I_j} - \sum _{j=1}^{N}\left( {v_h,(p^{(u)}_h)_x}\right) _{I_j} \nonumber \\&\qquad - \sum _{j=1}^{N}\left( {\{u_h\}[p^{(v)}_h]}\right) _{j-\frac{1}{2}} - \sum _{j=1}^{N}\left( {\{v_h\}[p^{(u)}_h]}\right) _{j-\frac{1}{2}} \nonumber \\&\quad = 0. \end{aligned}$$

  (B.10)

  In summary, by virtue of the definition of ${\mathcal {D}}^{\star }$, equalities in (B.4), (B.6) and (B.10) can be rewritten into the following concise forms

  $$\begin{aligned} {\mathcal {D}}^{\star }(u_h,p^{(u)}_h)&= 0, \nonumber \\ {\mathcal {D}}^{\star }(v_h,p^{(v)}_h)&= 0, \nonumber \\ {\mathcal {D}}^{\star }(u_h,p^{(v)}_h)+{\mathcal {D}}^{\star }(v_h,p^{(u)}_h)&= 0, \end{aligned}$$

  (B.11)

  Now, on account of the property of ${\mathcal {D}}^{\star }(\xi ,\zeta )$, namely

  $$\begin{aligned} {\mathcal {D}}^{\star }(\xi ,\zeta ) + {\mathcal {D}}^{\star }(\zeta ,\xi ) = 0, \end{aligned}$$

  and adding $2a{\mathcal {D}}^{\star }(u_h,p^{(u)}_h) + b({\mathcal {D}}^{\star }(u_h,p^{(v)}_h)+{\mathcal {D}}^{\star }(v_h,p^{(u)}_h)) + 2c{\mathcal {D}}^{\star }(v_h,p^{(v)}_h) = 0$ to ${\mathcal {J}}_c$, then we have

  $$\begin{aligned} {\mathcal {J}}_c(u_h,v_h;p^{(u)}_h,p^{(v)}_h) = 0. \end{aligned}$$

• (The dissipative case for ${\mathcal {J}}_d$) Using the similar strategies as in the last conservative case, the different choices of numerical fluxes

  $$\begin{aligned} {\widehat{p}}^{(\chi )}_h=(p^{(\chi )}_h)^+,\quad {\widehat{q}}^{(\chi )}_h=(q^{(\chi )}_h)^+,\quad \widehat{\chi _h}=\chi _h^-, \end{aligned}$$

  directly result in some inequalities comparing to the equalities in (B.11)

  $$\begin{aligned} {\mathcal {D}}^-(u_h,p^{(u)}_h)&\le 0, \nonumber \\ {\mathcal {D}}^-(v_h,p^{(v)}_h)&\le 0, \nonumber \\ {\mathcal {D}}^-(u_h,p^{(v)}_h)+{\mathcal {D}}^-(v_h,p^{(u)}_h)&\le 0. \end{aligned}$$

  (B.12)

  On account of the property, ${\mathcal {D}}^-(\xi ,\zeta )+{\mathcal {D}}^+(\zeta ,\xi )=0$, and the conditions $a,c > 0$ together with the extra assumption $b\ge 0$, then we have

  $$\begin{aligned}&{\mathcal {J}}_d(u_h,v_h;p^{(u)}_h,p^{(v)}_h)\nonumber \\&\qquad = 2a{\mathcal {D}}^+(p^{(u)}_h,u_h) + b({\mathcal {D}}^+(p^{(u)}_h,v_h)+{\mathcal {D}}^+(p^{(v)}_h,u_h)) + 2c{\mathcal {D}}^+(p^{(v)}_h,v_h) \nonumber \\&\qquad = -(2a{\mathcal {D}}^-(u_h,p^{(u)}_h) + b({\mathcal {D}}^-(u_h,p^{(v)}_h)+{\mathcal {D}}^-(v_h,p^{(u)}_h)) + 2c{\mathcal {D}}^-(v_h,p^{(v)}_h))\ge 0. \end{aligned}$$

$\square$