Local Energy Dissipation Rate Preserving Approximations to Driven Gradient Flows with Applications to Graphene Growth

Abstract

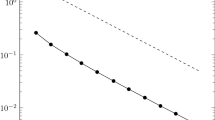
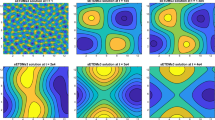
We develop a paradigm for developing local energy dissipation rate preserving (LEDRP) approximations to general gradient flow models driven by source terms. In driven gradient flow models, the deduced energy density transport equation possesses an indefinite source. Local energy-dissipation-rate preserving algorithms are devised to respect the mathematical structure of both the driven gradient flow model and its deduced energy density transport equation. The LEDRP algorithms are also global energy-dissipation-rate preserving under proper boundary conditions such as periodic boundary conditions. However, the contrary may not be true. We then apply the paradigm to a phase field model for growth of a graphene sheet to produce a set of LEDRP algorithms. Numerical refinement tests are conducted to confirm the convergence property of the new algorithms and simulations of graphene growth are demonstrated to benchmark against existing results in the literature.

Appendices

Appendix A: Proof of Some Theorems in Sect. 2

a. Proof for Theorem 2.1:  Multiplying $\mu$ and $\phi _t$ on both sides of the first equation and the second equation of (2.8), respectively, we obtain

$$\begin{aligned} \left\{ \begin{aligned}&\phi _t \mu = -\mu {\mathcal {M}}\mu ,\\&\phi _t\mu = \phi _t\sum _{i=0}^m (-1)^i \nabla ^i \frac{\partial f}{\partial \nabla ^i \phi }. \end{aligned} \right. \end{aligned}$$

(6.1)

Combining the two equations in (6.1), we have

$$\begin{aligned} -\mu {\mathcal {M}}\mu = \phi _t\sum _{i=0}^m (-1)^i \nabla ^i \frac{\partial f}{\partial \nabla ^i \phi }. \end{aligned}$$

(6.2)

Applying Lemma 2.1 and substituting all the terms on the right hand of (6.2), we arrive at

$$\begin{aligned} \begin{aligned} -\mu {\mathcal {M}}\mu = \sum _{i=0}^m (-1)^i\nabla \cdot \left( (-1)^{k-1}\sum _{k=1}^i \nabla ^{k-1}\phi _t\cdot \nabla ^{i-k}\frac{\partial f}{\partial \nabla ^i \phi } \right) +\sum _{i=0}^m\nabla ^i \phi _t \cdot \frac{\partial f}{\partial \nabla ^i \phi }. \end{aligned} \end{aligned}$$

(6.3)

Meanwhile, the time derivative of energy density (2.2) is given by

$$\begin{aligned} \frac{\mathrm {d}E}{\mathrm {d}t} = \sum _{i=0}^m\nabla ^i \phi _t \cdot \frac{\partial f}{\partial \nabla ^i \phi }. \end{aligned}$$

(6.4)

Inserting (6.4) into (6.3), we complete the proof.

b. Proof for Theorem 2.2:  Multiplying $\mu$ and $\phi _t$ on both sides of the first equation and the second equation in (2.15), respectively, we have

$$\begin{aligned} \left\{ \begin{aligned}&\phi _t \mu = -\mu {\mathcal {M}}\mu ,\\&\mu \phi _t= \left( \sum _{p=1}^{\frac{m+1}{2}} \Delta ^{p-1}k_p -\sum _{q=1}^{\frac{m+1}{2}} \nabla \Delta ^{q-1}{\mathbf {h}}_q\right) \cdot \phi _t. \end{aligned} \right. \end{aligned}$$

(6.5)

Using the Leibnitz rule repeatedly, we obtain

$$\begin{aligned} \begin{aligned}&\nabla \cdot \left[ \sum _{p=2}^{\frac{m+1}{2}} \sum _{l=0}^{2p-3}\left( \left( -1\right) ^{l+1}\nabla ^lk_p\cdot \nabla ^{2p-3-l}\phi _t \right) + \sum _{q=1}^{\frac{m+1}{2}} \sum _{r=0}^{2q-2}\left( \left( -1\right) ^{r+1}\nabla ^r{\mathbf {h}}_q\cdot \nabla ^{2q-2-r}\phi _t \right) \right] \\&+ \sum _{p=1}^{\frac{m+1}{2}} \left( k_p\cdot \Delta ^{p-1}\phi _t \right) + \sum _{q=1}^{\frac{m+1}{2}} \left( {\mathbf {h}}_q\cdot \nabla \Delta ^{q-1}\phi _t \right) = - \mu {\mathcal {M}}\mu . \end{aligned} \end{aligned}$$

(6.6)

It follows from the definition of the energy density (2.2)

$$\begin{aligned} \partial _t E = \sum _{p=1}^{\frac{m+1}{2}} \left( k_p\cdot \Delta ^{p-1}\phi _t \right) + \sum _{q=1}^{\frac{m+1}{2}} \left( {\mathbf {h}}_q\cdot \nabla \Delta ^{q-1}\phi _t \right) , \end{aligned}$$

(6.7)

substituting (6.7) into (6.6), we complete the proof.

c. Proof for Theorem 2.3:  Using Lemma 2.3m times, we have

$$\begin{aligned} -A_t \mu ^n{\mathcal {M}}A_t \mu ^n = \,&\nabla _h^+\cdot \left( \sum _{p=2}^{\frac{m+1}{2}}\sum _{l=0}^{p-2}\left( \delta _t^+\Delta _h^l\phi ^n\cdot \nabla _h^-\Delta _h^{p-2-l}A_t k_p^n-\delta _t^+\nabla _h^-\Delta _h^l\phi ^n\cdot \Delta _h^{p-2-l}A_t k_p^n \right) \right. \nonumber \\&\left. -\sum _{q=1}^{\frac{m+1}{2}}\delta _t^+\Delta _h^{q-1}\phi ^n \cdot A_t {\overline{{\mathbf {h}}}}_q^n \right. \nonumber \\&\left. +\sum _{q=2}^{\frac{m+1}{2}}\sum _{r=0}^{q-2}\left( -\delta _t^+\Delta _h^r\phi ^n\cdot \nabla _h^-\nabla _h^- \Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n +\delta _t^+\nabla _h^-\Delta _h^r\phi ^n\cdot \nabla _h^-\Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n \right) \right) \nonumber \\&+\sum _{p=1}^{\frac{m+1}{2}}A_t k_p^n\cdot \delta _t^+ \Delta _h^{p-1} \phi ^n +\sum _{q=1}^{\frac{m+1}{2}}A_t {\mathbf {h}}_q^n\cdot \delta _t^+\nabla _h^+ \Delta _h^{q-1} \phi ^n. \end{aligned}$$

(6.8)

It follows from the definition of the energy density, $E^n$, (2.18),

$$\begin{aligned} \begin{aligned} \delta _t^+E^n = \sum _{p=1}^{\frac{m+1}{2}}A_t k_p^n\cdot \delta _t^+ \Delta _h^{p-1} \phi ^n +\sum _{q=1}^{\frac{m+1}{2}}A_t {\mathbf {h}}_q^n\cdot \delta _t^+\nabla _h^+ \Delta _h^{q-1} \phi ^n. \end{aligned} \end{aligned}$$

(6.9)

Applying (6.9), we complete the proof.

d. Proof for Theorem 2.4:  With the aid of Lemma 2.4, we arrive at the conclusion readily.

e. Proof for Theorem 2.5: 

It follows from the definition of energy density, $E^n$, (2.34)

$$\begin{aligned} \begin{aligned} \delta _t^+E^n = \,&\sum _{p=1}^{\frac{m+1}{2}}A_t A_x^{m}A_y^{m}k_p^n\cdot \delta _t^+{\overline{\Delta }}_h^{p-1}A_x^{m-2p+2}A_y^{m-2p+2} \phi ^n\\&+\sum _{q=1}^{\frac{m+1}{2}}A_t A_x^{m}A_y^{m}{\mathbf {h}}_q^n\cdot \delta _t^+{\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1}A_x^{m-2q+1}A_y^{m-2q+1} \phi ^n. \end{aligned} \end{aligned}$$

(6.10)

With the aid of Lemma 2.5, we complete the proof.

f. Proof for Theorem 2.6:  Multiply $\mu ,\phi _t,q$ on both sides of the three equations in (2.46), respectively,

$$\begin{aligned} \left\{ \begin{aligned}&\mu \phi _t = -\mu {\mathcal {M}}\mu ,\\&\mu \phi _t= 2 \sum _{i=0}^{m} (-1)^i g_i(\epsilon )\cdot \nabla ^{2i}\phi \cdot \phi _t +2\sum _{i=0}^{m-1} (-1)^i \nabla ^i \left( q\cdot \frac{\partial q}{\partial \nabla ^i \phi }\right) \cdot \phi _t,\\&qq_t = \sum _{i=0}^{m-1} q\frac{\partial q}{\partial \nabla ^i \phi }\cdot \frac{\partial \nabla ^i \phi }{\partial t}. \end{aligned} \right. \end{aligned}$$

(6.11)

With Lemma 2.6, we derive from (6.11)

$$\begin{aligned} \begin{aligned} -\mu {\mathcal {M}}\mu&= 2\sum _{i=0}^m\left[ (-1)^ig_i(\epsilon )\nabla \left( \sum _{k=1}^i (-1)^{k-1}\nabla ^{k-1}\phi _t\cdot \nabla ^{2i-k}\phi \right) \right] \\&\quad +2\sum _{i=0}^{m-1}\left[ (-1)^i\nabla \left( (-1)^{k-1}\sum _{k=1}^i \nabla ^{k-1}\phi _t\cdot \nabla ^{i-k}\left( q\frac{\partial q}{\partial \nabla ^i \phi }\right) \right) \right] \\&\quad +2\sum _{i=0}^mg_i(\epsilon )\nabla ^i \phi _t \cdot \nabla ^i \phi _t+2qq_t, \end{aligned} \end{aligned}$$

(6.12)

Meanwhile, the time derivative of energy density E, (2.45), is given by

$$\begin{aligned} \frac{\mathrm {d}E}{\mathrm {d}t} = 2\sum _{i=0}^mg_i(\epsilon )\nabla ^i \phi _t \cdot \nabla ^i \phi _t+2qq_t. \end{aligned}$$

(6.13)

Inserting (6.13) into (6.12), we arrive at the conclusion.

Appendix B: LEDRP Algorithms in Sect. 2.2.3

Here we list the three LEDRP algorithms based on the energy quadratization technique presented in Sect. 2.2.3. We present the first algorithm based on the energy quadratization method next. Eliminating the intermediate variables in system (2.54)–(2.56), we arrive at the first LEDRP algorithm based on the EQ method as follows.

Algorithm 4

(EQ-LEDRP-I)

$$\begin{aligned} \left\{ \begin{aligned} \delta _t^+\phi ^n=\,&-2{\mathcal {M}} \left[ \sum _{i=0}^m (-1)^i g_i(\epsilon )\cdot A_t\Delta _h^i\phi ^n +\sum _{p=1}^{\frac{m+1}{2}} \Delta _h^{p-1}\left( A_tq^n\frac{\partial q^{n,\star }}{\partial \Delta _h^{p-1} \phi ^{n,\star }}\right) \right. \\&\left. \quad -\sum _{q=1}^{\frac{m-1}{2}} \nabla _h^-\Delta _h^{q-1}\left( A_tq^n\frac{\partial q^{n,\star }}{\partial \nabla _h^+\Delta _h^{q-1} \phi ^{n,\star }}\right) \right] ,\\ \delta _t^+q^n =\,&\sum _{p=1}^{\frac{m+1}{2}} \frac{\partial q^{n,\star }}{\partial \Delta _h^{p-1} \phi ^{n,\star }}\cdot \delta _t^+\Delta _h^{p-1}\phi ^n+\sum _{q=1}^{\frac{m-1}{2}} \frac{\partial q^{n,\star }}{\partial \nabla _h^+\Delta _h^{q-1} \phi ^{n,\star }}\cdot \delta _t^+\nabla _h^+\Delta _h^{q-1}\phi ^n. \end{aligned} \right. \end{aligned}$$

The transport equation for the discrete energy density in Algorithm 4 is given below.

Theorem 6.1

Model (2.54)–(2.56) satisfies the following discrete LEDL

$$\begin{aligned} \begin{aligned}&\delta _t^+ E^n+2\nabla _h^+\cdot \left( \sum _{p=2}^{\frac{m+1}{2}}\sum _{l=0}^{p-2}\left( \delta _t^+\Delta _h^l\phi ^n\cdot \nabla _h^-\Delta _h^{p-2-l}A_t k_p^n+\delta _t^+\nabla _h^-\Delta _h^l\phi ^n\cdot \Delta _h^{p-2-l}A_t k_p^n \right) \right. \\&\quad -\delta _t^+\phi ^n\cdot A_t {\overline{{\mathbf {h}}}}_1^n \\&\quad +\sum _{q=2}^{\frac{m-1}{2}}\left( \sum _{r=0}^{q-2}\left( -\delta _t^+\Delta _h^r\phi ^n\cdot \nabla _h^-\nabla _h^- \Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n +\delta _t^+\nabla _h^-\Delta _h^r\phi ^n\cdot \nabla _h^-\Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n \right) \right. \\&\quad \left. -\delta _t^+\Delta _h^{q-1}\phi ^n \cdot A_t {\overline{{\mathbf {h}}}}_q^n \right) \\&\quad \left. {+}\sum _{i=1 ~2\not \mid i}^m g_i(\epsilon )\left( {-}\sum _{l=\frac{i-1}{2}}^{i-1}\nabla _h^-\Delta _h^lA_t\phi ^n\cdot \delta _t^+\Delta _h^{i-1-l}\phi ^n{+} \sum _{l=\frac{i+1}{2}}^{i-1}\Delta _h^lA_t\phi ^n\cdot \delta _t^+\nabla _h^-\Delta _h^{i-1-l}\phi ^n \right) \right. \\&\quad \left. +\sum _{i=1~2| i}^m g_i(\epsilon ) \sum _{l=\frac{i}{2}}^{i-1}\left( \nabla _h^-\Delta _h^lA_t\phi ^n\cdot \delta _t^+\Delta _h^{i-1-l}\phi ^n- \Delta _h^lA_t\phi ^n\cdot \delta _t^+\nabla _h^-\Delta _h^{i-1-l}\phi ^n \right) \right) \\&\quad +A_t \mu ^n{\mathcal {M}}A_t \mu ^n=0, \end{aligned} \end{aligned}$$

with discrete energy density $E^n$ defined in (2.53).

Proof

We note that the time derivative of discrete energy density (2.53) is given by

$$\begin{aligned} \begin{aligned} \delta _t^+ E^n =\,&2\sum _{p=1}^{\frac{m+1}{2}}A_t k_p^n\cdot \delta _t^+ \Delta _h^{p-1} \phi ^n +2\sum _{q=1}^{\frac{m-1}{2}}A_t {\mathbf {h}}_q^n\cdot \delta _t^+\nabla _h^+ \Delta _h^{q-1} \phi ^n \\&+2\sum _{i=0~ 2|i}^m g_i(\epsilon )\Delta _h^{\frac{i}{2}}A_t \phi ^n\cdot \Delta _h^{\frac{i}{2}}\delta _t^+ \phi ^n+2\sum _{i=1 ~2\not \mid i}^m g_i(\epsilon )\nabla _h^+\Delta _h^{\frac{i}{2}}A_t \phi ^n\cdot \nabla _h^+\Delta _h^{\frac{i-1}{2}}\delta _t^+ \phi ^n. \end{aligned} \end{aligned}$$

(6.14)

Analogous to the proof of Theorem 2.3, we can easily arrive at the conclusion. $\square$

Then we present second LEDRP algorithm. Eliminating the intermediate variables, system (2.58)–(2.60) can be written into the following two-equation system.

Algorithm 5

(EQ-LEDRP-II)

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+\phi ^n= -2{\mathcal {M}} \left[ \sum _{i=0}^m (-1)^i g_i(\epsilon )\cdot A_t\Delta _h^i\phi ^n +\sum _{p=1}^{\frac{m+1}{2}} \Delta _h^{p-1}\left( A_tq^n\frac{\partial q^{n,\star }}{\partial \Delta _h^{p-1} \phi ^{n,\star }}\right) \right. \\&\quad \qquad \left. -\sum _{q=1}^{\frac{m-1}{2}} \nabla _h^+\Delta _h^{q-1}\left( A_tq^n\frac{\partial q^{n,\star }}{\partial \nabla _h^-\Delta _h^{q-1} \phi ^{n,\star }}\right) \right] ,\\&\delta _t^+q^n = \sum _{p=1}^{\frac{m+1}{2}} \frac{\partial q^{n,\star }}{\partial \Delta _h^{p-1} \phi ^{n,\star }}\cdot \delta _t^+\Delta _h^{p-1}\phi ^n+\sum _{q=1}^{\frac{m-1}{2}} \frac{\partial q^{n,\star }}{\partial \nabla _h^-\Delta _h^{q-1} \phi ^{n,\star }}\cdot \delta _t^+\nabla _h^-\Delta _h^{q-1}\phi ^n. \end{aligned} \right. \end{aligned}$$

The discrete energy density in Algorithm 5 obeys a transport equation given in the following theorem.

Theorem 6.2

Model (2.58)–(2.60) satisfies the following discrete local energy density transport equation

$$\begin{aligned} \begin{aligned}&\delta _t^+ E^n+2\nabla _h^-\cdot \left( \sum _{p=2}^{\frac{m+1}{2}}\sum _{l=0}^{p-2}\left( \delta _t^+\Delta _h^l\phi ^n\cdot \nabla _h^+\Delta _h^{p-2-l}A_t k_p^n- \delta _t^+\nabla _h^+\Delta _h^l\phi ^n\cdot \Delta _h^{p-2-l}A_t k_p^n \right) \right. \\&\quad -\delta _t^+\phi ^n\cdot A_t {\widetilde{{\mathbf {h}}}}_1^n \\&\quad +\sum _{q=2}^{\frac{m-1}{2}}\left( \sum _{r=0}^{q-2}\left( -\delta _t^+\Delta _h^r\phi ^n\cdot \Delta _h^{q-1-r}A_t {\widetilde{{\mathbf {h}}}}_q^n +\delta _t^+\nabla _h^+\Delta _h^r\phi ^n\cdot \nabla _h^+\Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n \right) \right. \\&\quad \left. -\delta _t^+\Delta _h^{q-1}\nabla _h^-\phi ^n \cdot A_t {\widetilde{{\mathbf {h}}}}_q^n\right) \\&\quad \left. +\sum _{i=1 ~2\not \mid i}^m g_i(\epsilon )\left( -\sum _{l=\frac{i-1}{2}}^{i-1}\nabla _h^+\Delta _h^lA_t\phi ^n\cdot \delta _t^+\Delta _h^{i-1-l}\phi ^n{+} \sum _{l=\frac{i+1}{2}}^{i-1}\Delta _h^lA_t\phi ^n\cdot \delta _t^+\nabla _h^+\Delta _h^{i-1-l}\phi ^n \right) \right. \\&\quad \left. +\sum _{i=1~2| i}^m g_i(\epsilon ) \sum _{l=\frac{i}{2}}^{i-1}\left( \nabla _h^+\Delta _h^lA_t\phi ^n\cdot \delta _t^+\Delta _h^{i-1-l}\phi ^n- \Delta _h^lA_t\phi ^n\cdot \delta _t^+\nabla _h^+\Delta _h^{i-1-l}\phi ^n \right) \right) \\&\quad +A_t \mu ^n{\mathcal {M}}A_t \mu ^n=0, \end{aligned} \end{aligned}$$

with discrete energy density $E^n$ defined in (2.57).

Analogously, we obtain the third LEDRP algorithm the same way.

Algorithm 6

(EQ-LEDRP-III)

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+A_x^{2m}A_y^{2m}\phi ^n = 2 \sum _{i=0}^m (-1)^i g_i(\epsilon )\cdot A_tA_x^{2m-2i}A_y^{2m-2i}{\overline{\Delta }}_h^i\phi ^n\\&\quad +2 \left[ \sum _{p=1}^{\frac{m+1}{2}} {\overline{\Delta }}_h^{p-1}A_x^{m-2p+2}A_y^{m-2p+2}A_tA_x^mA_y^mq^n\frac{\partial q^{n,\star }}{\partial {\overline{\Delta }}_h^{p-1} A_x^{m-2p+2}A_y^{m-2p+2}\phi ^{n,\star }} \right. \\&\left. \quad -\sum _{q=1}^{\frac{m-1}{2}} {\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1}A_x^{m-2q+2}A_y^{m-2q+2}A_tA_x^mA_y^mq^n\frac{\partial q^{n,\star }}{\partial {\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1} A_x^{m-2q+1}A_y^{m-2q+1}\phi ^{n,\star }} \right] ,\\&\delta _t^+A_x^mA_y^mq^n = \sum _{p=1}^{\frac{m+1}{2}} \frac{\partial q^{n,\star }}{\partial {\overline{\Delta }}_h^{p-1} A_x^{m-2p+2}A_y^{m-2p+2}\phi ^{n,\star }}\cdot \delta _t^+{\overline{\Delta }}_h^{p-1} A_x^{m-2p+2}A_y^{m-2p+2}\phi ^{n}\\&\quad +\sum _{q=1}^{\frac{m-1}{2}} \frac{\partial q^{n,\star }}{\partial {\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1} A_x^{m-2q+2}A_y^{m-2q+2}\phi ^{n,\star }}\cdot \delta _t^+{\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1} A_x^{m-2q+2}A_y^{m-2q+2}\phi ^n. \end{aligned} \right. \end{aligned}$$

Algorithm 6 has a discrete transport equation for the discrete energy density.

Theorem 6.3

Model (2.62)–(2.64) satisfies the following discrete energy density transport equation

$$\begin{aligned} \begin{aligned}&\delta _t^+ E^n+ 2\sum _{i=0~2|i}^{m}g_i(\epsilon ) \sum _{j=0}^{\frac{i}{2}}\left( \nabla _h^{[m-j]}\cdot \left( \delta _t^+{\overline{\nabla }}_h^j\phi ^n\cdot A_tA_x^{m-(2i-j)} A_y^{m-(2i-j)} {\overline{\nabla }}_h^{2i-j-1}\phi ^n \right) \right. \\&\quad \left. -\nabla _h^{[m-(2i-2-j)]}\cdot \left( A_t{\overline{\nabla }}_h^{2i-2-j}\phi ^n\cdot \delta _t^+A_x^{m-(j+2)} A_y^{m-(j+2)} {\overline{\nabla }}_h^{j+1}\phi ^n \right) \right) \\&\quad - 2\sum _{i=0~2\not \mid i}^{m}g_i(\epsilon )\left( \sum _{j=0}^{\frac{i+1}{2}} \nabla _h^{[m-j]}\cdot \left( \delta _t^+{\overline{\nabla }}_h^j\phi ^n\cdot A_tA_x^{m-(2i-j)} A_y^{m-(2i-j)} {\overline{\nabla }}_h^{2i-j-1}\phi ^n \right) \right. \\&\quad \left. -\sum _{j=0}^{\frac{i-1}{2}} \nabla _h^{[m-(2i-2-j)]}\cdot \left( A_t{\overline{\nabla }}_h^{2i-2-j}\phi ^n\cdot \delta _t^+A_x^{m-(j+2)} A_y^{m-(j+2)} {\overline{\nabla }}_h^{j+1}\phi ^n \right) \right) \\&\quad - 2\sum _{q=1}^{\frac{m-1}{2}} \sum _{l=0}^{q-1}\nabla _h^{[m-2l]}\cdot \left( {\overline{\Delta }}_h^{l}\delta _t^+\phi ^n\cdot {\overline{\Delta }}_h^{q-l-1}A_x^{m-2q+2l+1}A_y^{m-2q+2l+1}A_t {\mathbf {h}}_q^n \right) \\&\quad +2\sum _{q=2}^{\frac{m-1}{2}} \sum _{l=0}^{q-2} \nabla _h^{[m-2l-1]}\cdot \left( {\overline{\nabla }}_h{\overline{\Delta }}_h^{l}A_t{\mathbf {h}}_q^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{q-l-2}A_x^{m-2q+2l+2} A_y^{m-2q+2l+2}\delta _t^+\phi ^n \right) \\&\quad +2\sum _{p=2}^{\frac{m+1}{2}}\left\{ \sum _{r=0}^{p-2}\nabla _h^{[m-2r]}\cdot \left( {\overline{\Delta }}_h^{r}\delta _t^+\phi ^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{p-r-2}A_x^{m-2p+2r+2} A_y^{m-2p+2r+2}A_tk_p^n\right. \right. \\&\quad \left. \left. -{\overline{\Delta }}_h^{r}A_tk_p^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{p-r-2}A_x^{m-2p+2r+2} A_y^{m-2p+2r+2}\delta _t^+\phi ^n \right) \right\} \\&\quad + A_tA_x^mA_y^m\mu ^n{\mathcal {M}}A_tA_x^mA_y^m\mu ^n=0, \end{aligned} \end{aligned}$$

with $E^n$ the discrete energy density defined by (2.61).

Proof

We again omit the proof here. $\square$

Appendix C: LEDRP Algorithms for Driven Gradient Flows

We list the algorithms and the corresponding discrete energy density transport equations for the driven gradient flow system in the following.

Algorithm 7

(LEDRP-I for driven gradient flows) Given the free energy density in (2.18), the intermediate variables (2.19)–(2.20), the discrete system reads as follows

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+ \phi ^n = -{\mathcal {M}}A_t\mu ^n + A_tg(\phi ^n),\\&A_t\mu ^n = \sum _{p=1}^{\frac{m+1}{2}}\Delta _h^{p-1}A_t k_p^n - \nabla _h^-\sum _{q=1}^{\frac{m+1}{2}}\Delta _h^{q-1}A_t {\mathbf {h}}_q^n. \end{aligned} \right. \end{aligned}$$

(6.15)

Next we state the local energy dissipation rate property for Algorithm 7 as follows.

Theorem 6.4

Model (2.19)–(2.20), (6.15) has the following discrete energy density transport equation

$$\begin{aligned} \begin{aligned}&\delta _t^+ E^n+\nabla _h^+\cdot \left( \sum _{p=2}^{\frac{m+1}{2}}\sum _{l=0}^{p-2}\left( \delta _t^+\Delta _h^l\phi ^n\cdot \nabla _h^-\Delta _h^{p-2-l}A_t k_p^n-\delta _t^+\nabla _h^-\Delta _h^l\phi ^n\cdot \Delta _h^{p-2-l}A_t k_p^n \right) \right. \\&\quad \left. -\sum _{q=1}^{\frac{m+1}{2}}\delta _t^+\Delta _h^{q-1}\phi ^n \cdot A_t {\overline{{\mathbf {h}}}}_q^n \right. \\&\quad \left. +\sum _{q=2}^{\frac{m+1}{2}}\sum _{r=0}^{q-2}\left( -\delta _t^+\Delta _h^r\phi ^n\cdot \nabla _h^-\nabla _h^- \Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n +\delta _t^+\nabla _h^-\Delta _h^r\phi ^n\cdot \nabla _h^-\Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n \right) \right) \\&\quad +A_t \mu ^n{\mathcal {M}}A_t \mu ^n=A_tg(\phi ^n)\cdot A_t\mu ^n, \end{aligned} \end{aligned}$$

with E the discrete energy density defined by (2.18).

Algorithm 8

(LEDRP-II for driven gradient flows) Given the free energy density (2.28), the intermediate variables (2.29)–(2.30), the discrete gradient flow system reads as follows

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+ \phi ^n = -{\mathcal {M}}A_t\mu ^n+ A_tg(\phi ^n),\\&A_t\mu ^n = \sum _{p=1}^{\frac{m+1}{2}}\Delta _h^{p-1}A_t k_p^n - \nabla _h^+\sum _{q=1}^{\frac{m+1}{2}}\Delta _h^{q-1}A_t {\mathbf {h}}_q^n. \end{aligned} \right. \end{aligned}$$

(6.16)

Theorem 6.5

Model (2.29)–(2.30), (6.16) has the following discrete energy density transport equation

$$\begin{aligned} \begin{aligned}&\delta _t^+ E^n+\nabla _h^-\cdot \left( \sum _{p=2}^{\frac{m+1}{2}}\sum _{l=0}^{p-2}\left( \delta _t^+\Delta _h^l\phi ^n\cdot \nabla _h^+\Delta _h^{p-2-l}A_t k_p^n- \delta _t^+\nabla _h^+\Delta _h^l\phi ^n\cdot \Delta _h^{p-2-l}A_t k_p^n \right) \right. \\&\quad \left. -\sum _{q=1}^{\frac{m+1}{2}}\delta _t^+\Delta _h^{q-1}\phi ^n \cdot A_t {\widetilde{{\mathbf {h}}}}_q^n \right. \\&\quad \left. +\sum _{q=2}^{\frac{m+1}{2}}\sum _{r=0}^{q-2}\left( -\delta _t^+\Delta _h^r\phi ^n\cdot \Delta _h^{q-1-r}A_t {\widetilde{{\mathbf {h}}}}_q^n +\delta _t^+\nabla _h^+\Delta _h^r\phi ^n\cdot \nabla _h^+\Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n \right) \right) \\&\quad +A_t \mu ^n{\mathcal {M}}A_t \mu ^n=A_tg(\phi ^n)\cdot A_t\mu ^n, \end{aligned} \end{aligned}$$

with E the discrete energy density defined by (2.28).

Algorithm 9

(LEDRP-III for driven gradient flows) Given the free energy density in (2.34), the intermediate variables (2.35)–(2.36), the discrete gradient flow system reads as follows

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+ A_x^mA_y^m \phi ^n = -{\mathcal {M}}A_tA_x^mA_y^m\mu ^n+A_tg(A_x^mA_y^m\phi ^n),\\&A_tA_x^mA_y^m\mu ^n = \sum _{p=1}^{\frac{m+1}{2}}{\overline{\Delta }}_h^{p-1}A_t A_x^{m-2p+2}A_y^{m-2p+2} k_p^n - \sum _{q=1}^{\frac{m+1}{2}}{\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1}A_t A_x^{m-2q+1}A_y^{m-2q+1} {\mathbf {h}}_q^n.\qquad \end{aligned} \right. \end{aligned}$$

(6.17)

Theorem 6.6

Model (2.35)–(2.36), (6.17) has the following energy density transport equation

$$\begin{aligned} \begin{aligned}&\delta _t^+ E^n- \sum _{q=1}^{\frac{m+1}{2}} \sum _{l=0}^{q-1}\nabla _h^{[m-2l]}\cdot \left( {\overline{\Delta }}_h^{l}\delta _t^+\phi ^n\cdot {\overline{\Delta }}_h^{q-l-1}A_x^{m-2q+2l+1}A_y^{m-2q+2l+1}A_t {\mathbf {h}}_q^n \right) \\&\quad +\sum _{q=2}^{\frac{m+1}{2}} \sum _{l=0}^{q-2} \nabla _h^{[m-2l-1]}\cdot \left( {\overline{\nabla }}_h{\overline{\Delta }}_h^{l}A_t{\mathbf {h}}_q^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{q-l-2}A_x^{m-2q+2l+2}A_y^{m-2q+2l+2}\delta _t^+\phi ^n \right) \\&\quad +\sum _{p=2}^{\frac{m+1}{2}}\Big \{ \sum _{r=0}^{p-2}\nabla _h^{[m-2r]}\cdot \left( {\overline{\Delta }}_h^{r}\delta _t^+\phi ^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{p-r-2}A_x^{m-2p+2r+2}A_y^{m-2p+2r+2}A_tk_p^n \right. \\&\quad \left. -{\overline{\Delta }}_h^{r}A_tk_p^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{p-r-2}A_x^{m-2p+2r+2}A_y^{m-2p+2r+2}\delta _t^+\phi ^n \right) \Big \}\\&\quad + A_tA_x^mA_y^m\mu ^n{\mathcal {M}}A_tA_x^mA_y^m\mu ^n=A_tg(A_x^mA_y^m\phi ^n)\cdot A_tA_x^mA_y^m\mu ^n, \end{aligned} \end{aligned}$$

with E the discrete energy density defined by (2.34).

In the following, we list the algorithms and the discrete energy density transport equation for the driven gradient flow system based on the EQ technique.

Algorithm 10

(EQ-LEDRP-I for driven gradient flows) Given the free energy density in (2.53) and intermediate variables (2.54)–(2.55), we discritize driven gradient flow (3.5) as follows

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+\phi ^n= -{\mathcal {M}}A_t\mu ^n+g(\phi ^{n,\star }),\\&A_t\mu ^n = 2 \sum _{i=0}^m (-1)^i g_i(\epsilon )\cdot A_t\Delta _h^i\phi ^n +2 \left[ \sum _{p=1}^{\frac{m+1}{2}} \Delta _h^{p-1}A_tk_p -\sum _{q=1}^{\frac{m-1}{2}} \nabla _h^-\Delta _h^{q-1}A_t{\mathbf {h}}_q \right] ,\\&\delta _t^+q^n = \sum _{p=1}^{\frac{m+1}{2}} \frac{\partial q^{n,\star }}{\partial \Delta _h^{p-1} \phi ^{n,\star }}\cdot \delta _t^+\Delta _h^{p-1}\phi ^n+\sum _{q=1}^{\frac{m-1}{2}} \frac{\partial q^{n,\star }}{\partial \nabla _h^+\Delta _h^{q-1} \phi ^{n,\star }}\cdot \delta _t^+\nabla _h^+\Delta _h^{q-1}\phi ^n.\nonumber \end{aligned} \right. \\ \end{aligned}$$

(6.18)

Theorem 6.7

System (6.18) admits the following discrete energy density transport equation

$$\begin{aligned}&\delta _t^+ E^n+2\nabla _h^+\cdot \left( \sum _{p=2}^{\frac{m+1}{2}}\sum _{l=0}^{p-2}\left( \delta _t^+\Delta _h^l\phi ^n\cdot \nabla _h^-\Delta _h^{p-2-l}A_t k_p^n+\delta _t^+\nabla _h^-\Delta _h^l\phi ^n\cdot \Delta _h^{p-2-l}A_t k_p^n \right) \right. \\&\quad -\delta _t^+\phi ^n\cdot A_t {\overline{{\mathbf {h}}}}_1^n \\&\quad +\sum _{q=2}^{\frac{m-1}{2}}\left( \sum _{r=0}^{q-2}\left( -\delta _t^+\Delta _h^r\phi ^n\cdot \nabla _h^-\nabla _h^- \Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n +\delta _t^+\nabla _h^-\Delta _h^r\phi ^n\cdot \nabla _h^-\Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n \right) \right. \\&\quad \left. -\delta _t^+\Delta _h^{q-1}\phi ^n \cdot A_t {\overline{{\mathbf {h}}}}_q^n \right) \\&\quad \left. +\sum _{i=1 ~2\not \mid i}^m g_i(\epsilon )\left( -\sum _{l=\frac{i-1}{2}}^{i-1}\nabla _h^-\Delta _h^lA_t\phi ^n\cdot \delta _t^+\Delta _h^{i-1-l}\phi ^n+ \sum _{l=\frac{i+1}{2}}^{i-1}\Delta _h^lA_t\phi ^n\cdot \delta _t^+\nabla _h^-\Delta _h^{i-1-l}\phi ^n \right) \right. \\&\quad \left. +\sum _{i=1~2| i}^m g_i(\epsilon ) \sum _{l=\frac{i}{2}}^{i-1}\left( \nabla _h^-\Delta _h^lA_t\phi ^n\cdot \delta _t^+\Delta _h^{i-1-l}\phi ^n- \Delta _h^lA_t\phi ^n\cdot \delta _t^+\nabla _h^-\Delta _h^{i-1-l}\phi ^n \right) \right) \\&\quad +A_t \mu ^n{\mathcal {M}}A_t \mu ^n= g(\phi ^{n,\star })A_t \mu ^n, \end{aligned}$$

Algorithm 11

(EQ-LEDRP-II for driven gradient flows) Given the discrete energy density in (2.57), and intermediate variables (2.58)–(2.59), we discretize driven gradient flow (3.5) as follows

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+\phi ^n= -{\mathcal {M}}A_t\mu ^n+g(\phi ^{n,\star }),\\&A_t\mu ^n = 2 \sum _{i=0}^m (-1)^i g_i(\epsilon )\cdot A_t\Delta _h^i\phi ^n +2 \left[ \sum _{p=1}^{\frac{m+1}{2}} \Delta _h^{p-1}A_tk_p -\sum _{q=1}^{\frac{m-1}{2}} \nabla _h^+\Delta _h^{q-1}A_t{\mathbf {h}}_q \right] ,\\&\delta _t^+q^n = \sum _{p=1}^{\frac{m+1}{2}} \frac{\partial q^{n,\star }}{\partial \Delta _h^{p-1} \phi ^{n,\star }}\cdot \delta _t^+\Delta _h^{p-1}\phi ^n+\sum _{q=1}^{\frac{m-1}{2}} \frac{\partial q^{n,\star }}{\partial \nabla _h^-\Delta _h^{q-1} \phi ^{n,\star }}\cdot \delta _t^+\nabla _h^-\Delta _h^{q-1}\phi ^n.\nonumber \end{aligned} \right. \!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(6.19)

Theorem 6.8

Model (6.19) satisfies the following discrete energy density transport equation

$$\begin{aligned} \begin{aligned}&\delta _t^+ E^n+2\nabla _h^-\cdot \left( \sum _{p=2}^{\frac{m+1}{2}}\sum _{l=0}^{p-2}\left( \delta _t^+\Delta _h^l\phi ^n\cdot \nabla _h^+\Delta _h^{p-2-l}A_t k_p^n- \delta _t^+\nabla _h^+\Delta _h^l\phi ^n\cdot \Delta _h^{p-2-l}A_t k_p^n \right) \right. \\&\quad -\delta _t^+\phi ^n\cdot A_t {\widetilde{{\mathbf {h}}}}_1^n \\&\quad +\sum _{q=2}^{\frac{m-1}{2}}\left( \sum _{r=0}^{q-2}\left( -\delta _t^+\Delta _h^r\phi ^n\cdot \Delta _h^{q-1-r}A_t {\widetilde{{\mathbf {h}}}}_q^n +\delta _t^+\nabla _h^+\Delta _h^r\phi ^n\cdot \nabla _h^+\Delta _h^{q-2-r}A_t {\mathbf {h}}_q^n \right) \right. \\&\quad \left. -\delta _t^+\Delta _h^{q-1}\nabla _h^-\phi ^n \cdot A_t {\widetilde{{\mathbf {h}}}}_q^n\right) \\&\quad \left. +\sum _{i=1 ~2\not \mid i}^m g_i(\epsilon )\left( -\sum _{l=\frac{i-1}{2}}^{i-1}\nabla _h^+\Delta _h^lA_t\phi ^n\cdot \delta _t^+\Delta _h^{i-1-l}\phi ^n+ \sum _{l=\frac{i+1}{2}}^{i-1}\Delta _h^lA_t\phi ^n\cdot \delta _t^+\nabla _h^+\Delta _h^{i-1-l}\phi ^n \right) \right. \\&\quad \left. +\sum _{i=1~2| i}^m g_i(\epsilon ) \sum _{l=\frac{i}{2}}^{i-1}\left( \nabla _h^+\Delta _h^lA_t\phi ^n\cdot \delta _t^+\Delta _h^{i-1-l}\phi ^n- \Delta _h^lA_t\phi ^n\cdot \delta _t^+\nabla _h^+\Delta _h^{i-1-l}\phi ^n \right) \right) \\&\quad +A_t \mu ^n{\mathcal {M}}A_t \mu ^n=g(\phi ^{n,\star })A_t\mu ^n, \end{aligned} \end{aligned}$$

with discrete energy density $E^n$ defined in (2.57).

Algorithm 12

(EQ-LEDRP-III for driven gradient flows) Given the discrete energy density in (2.61), and intermediate variables (2.62)–(2.63), we discretize system (3.5) as follows

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+A_x^mA_y^m\phi ^n= -{\mathcal {M}}A_tA_x^mA_y^m\mu ^n+g(A_x^{m}A_y^{m}\phi ^{n,\star }),\\&A_tA_x^mA_y^m\mu ^n = 2 \sum _{i=0}^m (-1)^i g_i(\epsilon )\cdot A_tA_x^{m-2i}A_y^{m-2i}{\overline{\Delta }}_h^i\phi ^n\\&\quad +2 \left[ \sum _{p=1}^{\frac{m+1}{2}} {\overline{\Delta }}_h^{p-1}A_tA_x^{m-2p+2}A_y^{m-2p+2}k_p^n -\sum _{q=1}^{\frac{m-1}{2}} {\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1}A_tA_x^{m-2q+2}A_y^{m-2q+2}{\mathbf {h}}_q^n \right] ,\\&\delta _t^+A_x^mA_y^mq^n = \sum _{p=1}^{\frac{m+1}{2}} \frac{\partial q^{n,\star }}{\partial {\overline{\Delta }}_h^{p-1} A_x^{m-2p+2}A_y^{m-2p+2}\phi ^{n,\star }}\cdot \delta _t^+{\overline{\Delta }}_h^{p-1} A_x^{m-2p+2}A_y^{m-2p+2}\phi ^{n}\\&\quad +\sum _{q=1}^{\frac{m-1}{2}} \frac{\partial q^{n,\star }}{\partial {\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1} A_x^{m-2q+2}A_y^{m-2q+2}\phi ^{n,\star }}\cdot \delta _t^+{\overline{\nabla }}_h{\overline{\Delta }}_h^{q-1} A_x^{m-2q+2}A_y^{m-2q+2}\phi ^n.\nonumber \end{aligned} \right. \\ \end{aligned}$$

(6.20)

Theorem 6.9

Model (6.20) satisfies the following discrete energy density transport equation

$$\begin{aligned} \begin{aligned}&\delta _t^+ E^n+ 2\sum _{i=0~2|i}^{m}g_i(\epsilon ) \sum _{j=0}^{\frac{i}{2}}\left( \nabla _h^{[m-j]}\cdot \left( \delta _t^+{\overline{\nabla }}_h^j\phi ^n\cdot A_tA_x^{m-(2i-j)} A_y^{m-(2i-j)} {\overline{\nabla }}_h^{2i-j-1}\phi ^n \right) \right. \\&\quad \left. -\nabla _h^{[m-(2i-2-j)]}\cdot \left( A_t{\overline{\nabla }}_h^{2i-2-j}\phi ^n\cdot \delta _t^+A_x^{m-(j+2)} A_y^{m-(j+2)} {\overline{\nabla }}_h^{j+1}\phi ^n \right) \right) \\&\quad - 2\sum _{i=0~2\not \mid i}^{m}g_i(\epsilon )\left( \sum _{j=0}^{\frac{i+1}{2}} \nabla _h^{[m-j]}\cdot \left( \delta _t^+{\overline{\nabla }}_h^j\phi ^n\cdot A_tA_x^{m-(2i-j)} A_y^{m-(2i-j)} {\overline{\nabla }}_h^{2i-j-1}\phi ^n \right) \right. \\&\quad \left. -\sum _{j=0}^{\frac{i-1}{2}} \nabla _h^{[m-(2i-2-j)]}\cdot \left( A_t{\overline{\nabla }}_h^{2i-2-j}\phi ^n\cdot \delta _t^+A_x^{m-(j+2)} A_y^{m-(j+2)} {\overline{\nabla }}_h^{j+1}\phi ^n \right) \right) \\&\quad - 2\sum _{q=1}^{\frac{m-1}{2}} \sum _{l=0}^{q-1}\nabla _h^{[m-2l]}\cdot \left( {\overline{\Delta }}_h^{l}\delta _t^+\phi ^n\cdot {\overline{\Delta }}_h^{q-l-1}A_x^{m-2q+2l+1}A_y^{m-2q+2l+1}A_t {\mathbf {h}}_q^n \right) \\&\quad +2\sum _{q=2}^{\frac{m-1}{2}} \sum _{l=0}^{q-2} \nabla _h^{[m-2l-1]}\cdot \left( {\overline{\nabla }}_h{\overline{\Delta }}_h^{l}A_t{\mathbf {h}}_q^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{q-l-2}A_x^{m-2q+2l+2}A_y^{m-2q+2l+2}\delta _t^+\phi ^n \right) \\&\quad +2\sum _{p=2}^{\frac{m+1}{2}}\left\{ \sum _{r=0}^{p-2}\nabla _h^{[m-2r]}\cdot \left( {\overline{\Delta }}_h^{r}\delta _t^+\phi ^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{p-r-2}A_x^{m-2p+2r+2}A_y^{m-2p+2r+2}A_tk_p^n \right. \right. \\&\quad \left. \left. -{\overline{\Delta }}_h^{r}A_tk_p^n\cdot {\overline{\nabla }}_h{\overline{\Delta }}_h^{p-r-2}A_x^{m-2p+2r+2}A_y^{m-2p+2r+2}\delta _t^+\phi ^n \right) \right\} \\&\quad + A_tA_x^mA_y^m\mu ^n{\mathcal {M}}A_tA_x^mA_y^m\mu ^n= g\big (A_x^mA_y^m\phi ^{n,\star }\big )A_tA_x^mA_y^m\mu ^n, \end{aligned} \end{aligned}$$

with $E^n$ the discrete energy density defined by (2.61).

Appendix D: Proof of Some Theorems in Sect. 4

a. Proof for Theorem 4.1:  Multiplying $\varvec{\mu }$ and ${\mathbf {u}}_t$ on both sides of the first and the second equation in (4.9), we have

$$\begin{aligned} \left\{ \begin{aligned}&{\mathbf {u}}_t\cdot \varvec{\mu } = -\varvec{\mu }^T\cdot \varvec{M}(\Theta ) \cdot \varvec{\mu } +{\mathbf {g}}({\mathbf {u}})\cdot \varvec{\mu },\\&\varvec{\mu }\cdot {\mathbf {u}}_t = \left( \begin{matrix} -\epsilon ^2\nabla \cdot \left[ \xi _{s,n}(\Theta )^2 \nabla \phi \right] +\epsilon ^2\partial _x\left[ \xi _{s,n}(\Theta )\xi _{s,n}'(\Theta )\partial _y\phi \right] \ \epsilon ^2\partial _y\left[ \xi _{s,n}(\Theta )\xi _{s,n}'(\Theta )\partial _x\phi \right] +f'(\phi ) \frac{u}{\tau _v}-\nabla \cdot \left( D\cdot \nabla u \right) \end{matrix}\right) \\&\quad \quad \quad \quad \cdot {\mathbf {u}}_t. \end{aligned} \right. \end{aligned}$$

(6.21)

Using derivative rule, we arrive at

$$\begin{aligned} \begin{aligned}&\left[ \epsilon ^2\xi _{s,n}(\Theta )^2 \nabla \phi + \left( \begin{matrix} -\epsilon ^2 \xi _{s,n}(\Theta )\xi _{s,n}'(\Theta )\partial _y \phi \\ \epsilon ^2 \xi _{s,n}(\Theta )\xi _{s,n}'(\Theta )\partial _x \phi \end{matrix} \right) \right] \cdot \nabla \phi _t+f'(\phi )\phi _t +\frac{u}{\tau _v} u_t\\&+\nabla u^T\cdot D \cdot \nabla u_t +\nabla \cdot \left[ - \epsilon ^2\xi _{s,n}(\Theta )^2 \nabla \phi \cdot \phi _t+ \left( \begin{matrix} \epsilon ^2 \xi _{s,n}(\Theta )\xi _{s,n}'(\Theta )\partial _y \phi \\ -\epsilon ^2 \xi _{s,n}(\Theta )\xi _{s,n}'(\Theta )\partial _x \phi \end{matrix} \right) \cdot \phi _t-D\cdot \nabla u \cdot u_t \right] \\&+\varvec{\mu }^T\cdot \varvec{M}(\Theta ) \cdot \varvec{\mu } ={\mathbf {g}}({\mathbf {u}})\cdot \varvec{\mu }, \end{aligned} \end{aligned}$$

(6.22)

from the definition of the local free energy, (4.13), we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}E}{\mathrm {d}t}&= \left[ \epsilon ^2\xi _{s,n}(\Theta )^2 \nabla \phi + \left( \begin{matrix} -\epsilon ^2 \xi _{s,n}(\Theta )\xi _{s,n}'(\Theta )\partial _y \phi \\ \epsilon ^2 \xi _{s,n}(\Theta )\xi _{s,n}'(\Theta )\partial _x \phi \end{matrix} \right) \right] \cdot \nabla \phi _t+f'(\phi )\phi _t\\&\quad +\frac{u}{\tau _v} u_t+ \nabla u^T\cdot D\cdot \nabla u_t, \end{aligned} \end{aligned}$$

(6.23)

Combing the results, we complete the proof.

b. Proof of Theorem 4.2:  The proof is similar to that of Theorem 4.1 and is thus omitted.

c. Proof of Theorem 4.3:  Multiplying $A_t \varvec{\mu }^n$ and $\delta _t^+ {\mathbf {u}}^n$ on both sides of the second and third line in (4.28), respectively, we have

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+ {\mathbf {u}}^n \cdot A_t \varvec{\mu }^n = -(A_t {\varvec{\mu }^n}) ^T\cdot \varvec{M}\left( {\overline{\Theta }}^{n,\star } \right) \cdot A_t\varvec{\mu ^n}+{\mathbf {g}}({\mathbf {u}}^{n,\star })\cdot A_t \varvec{\mu }^n ,\\&A_t \varvec{\mu }^n\cdot \delta _t^+ {\mathbf {u}}^n = A_t\varvec{k}^n\cdot \delta _t^+ {\mathbf {u}}^n-\nabla _h^-\cdot A_t \varvec{H}^n\cdot \delta _t^+ {\mathbf {u}}^n. \end{aligned} \right. \end{aligned}$$

(6.24)

Inserting the first and second equation which are in the first line of (4.28) into (6.24), we obtain

$$\begin{aligned} \begin{aligned}&\left( \begin{array}{l} \frac{1}{2}A_t V^n\cdot P^{n,\star } \\ \frac{A_t u^n}{\tau _v} \end{array} \right) \cdot \delta _t^+ {\mathbf {u}}^n - \nabla _h^-\cdot \left( \begin{array}{l} \epsilon ^2 A_tU^n\cdot \varvec{R}^{n,\star } \\ D\cdot \nabla _h^+A_t u^n \end{array} \right) \cdot \delta _t^+ {\mathbf {u}}^n\\&= -(A_t {\varvec{\mu }^n}) ^T\cdot \varvec{M}\left( {\overline{\Theta }}^{n,\star } \right) \cdot A_t\varvec{\mu ^n}+{\mathbf {g}}({\mathbf {u}}^{n,\star })\cdot A_t \varvec{\mu }^n . \end{aligned} \end{aligned}$$

(6.25)

With the aid of Lemma 2.3, we have

$$\begin{aligned} \begin{aligned}&\epsilon ^2 A_t U^n\cdot \varvec{R}^{n,\star }\cdot \delta _t^+\nabla _h^+\phi ^n+\frac{1}{2}A_t V^n \cdot P^{n,\star }\cdot \delta _t^+\phi ^n\\&\quad +\frac{A_t u^n}{\tau _v}\delta _t^+ u^n+(\delta _t^+\nabla _h^+ u^n)^T\cdot D\cdot \nabla _h^+A_t u^n- \nabla _h^+\cdot \left( A_t \overline{\varvec{H}}^n\cdot \delta _t^+{\mathbf {u}}^n \right) \\&\quad +\left( A_t \varvec{\mu }^n\right) ^T\cdot \varvec{M}({\overline{\Theta }}^{n,\star })\cdot A_t \varvec{\mu }^n = {\mathbf {g}}\left( {\mathbf {u}}^{n,\star } \right) \cdot A_t \varvec{\mu }^n.\\ \end{aligned} \end{aligned}$$

(6.26)

Inserting the last two equations of (4.28) into the time derivative of local energy (4.27), we arrive at

$$\begin{aligned} \begin{aligned} \delta _t^+E^n = ~&\epsilon ^2 A_t U^n\cdot \varvec{R}^{n,\star }\cdot \delta _t^+\nabla _h^+\phi ^n+\frac{1}{2}A_t V^n \cdot P^{n,\star }\cdot \delta _t^+\phi ^n\\&+\frac{A_t u^n}{\tau _v}\delta _t^+ u^n+(\delta _t^+\nabla _h^+ u^n)^T\cdot D\cdot \nabla _h^+A_t u^n. \end{aligned} \end{aligned}$$

(6.27)

Combining all the results, we complete the proof.

d. Proof of Theorem 4.4:  We multiply $A_t \varvec{\mu }^n$ and $\delta _t^+ {\mathbf {u}}^n$ on both sides of the second and third equation in (4.34), respectively, we have

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+ {\mathbf {u}}^n \cdot A_t \varvec{\mu }^n = -(A_t {\varvec{\mu }^n}) ^T\cdot \varvec{M}\left( {\overline{\Theta }}^{n,\star } \right) \cdot A_t\varvec{\mu ^n}+{\mathbf {g}}({\mathbf {u}}^{n,\star })\cdot A_t \varvec{\mu }^n ,\\&A_t \varvec{\mu }^n\cdot \delta _t^+ {\mathbf {u}}^n = A_t\varvec{k}^n\cdot \delta _t^+ {\mathbf {u}}^n-\nabla _h^+\cdot A_t \varvec{H}^n\cdot \delta _t^+ {\mathbf {u}}^n, \end{aligned} \right. \end{aligned}$$

(6.28)

Inserting the first and second equation which are in the first line of (4.34) into (6.28), we have

$$\begin{aligned} \begin{aligned}&\left( \begin{array}{l} \frac{1}{2}A_t V^n\cdot P^{n,\star } \\ \frac{A_t u^n}{\tau _v} \end{array} \right) \cdot \delta _t^+ {\mathbf {u}}^n - \nabla _h^+\cdot \left( \begin{array}{l} \epsilon ^2 A_tU^n\cdot \varvec{R}^{n,\star } \\ D\cdot \nabla _h^-A_t u^n \end{array} \right) \cdot \delta _t^+ {\mathbf {u}}^n\\&= -(A_t {\varvec{\mu }^n}) ^T\cdot \varvec{M}\left( {\overline{\Theta }}^{n,\star } \right) \cdot A_t\varvec{\mu ^n}+{\mathbf {g}}({\mathbf {u}}^{n,\star })\cdot A_t \varvec{\mu }^n . \end{aligned} \end{aligned}$$

(6.29)

With the aid of Lemma 2.4, we have

$$\begin{aligned} \begin{aligned}&\epsilon ^2 A_t U^n\cdot \varvec{R}^{n,\star }\cdot \delta _t^+\nabla _h^-\phi ^n+\frac{1}{2}A_t V^n \cdot P^{n,\star }\cdot \delta _t^+\phi ^n\\&\quad +\frac{A_t u^n}{\tau _v}\delta _t^+ u^n+(\delta _t^+\nabla _h^- u^n)^T\cdot D\cdot \nabla _h^-A_t u^n- \nabla _h^-\cdot \left( A_t \widetilde{\varvec{H}}^n\cdot \delta _t^+{\mathbf {u}}^n \right) \\&\quad +\left( A_t \varvec{\mu }^n\right) ^T\cdot \varvec{M}({\overline{\Theta }}^{n,\star })\cdot A_t \varvec{\mu }^n = {\mathbf {g}}\left( {\mathbf {u}}^{n,\star } \right) \cdot A_t \varvec{\mu }^n.\\ \end{aligned} \end{aligned}$$

(6.30)

Inserting the last two equations of (4.34) into the time derivative of energy density (4.33), we arrive at

$$\begin{aligned} \begin{aligned} \delta _t^+E^n = ~&\epsilon ^2 A_t U^n\cdot \varvec{R}^{n,\star }\cdot \delta _t^+\nabla _h^-\phi ^n+\frac{1}{2}A_t V^n \cdot P^{n,\star }\cdot \delta _t^+\phi ^n \\&+\frac{A_t u^n}{\tau _v}\delta _t^+ u^n+(\delta _t^+\nabla _h^- u^n)^T\cdot D\cdot \nabla _h^-A_t u^n. \end{aligned} \end{aligned}$$

(6.31)

Inserting (6.31) into (6.30), we complete the proof.

e. Proof of Theorem 4.5:  Multiplying $A_tA_xA_y\varvec{\mu }^n$, $\delta _t^+A_xA_y{\mathbf {u}}^n$ on both sides of the second and third equation in(4.39), we obtain

$$\begin{aligned} \left\{ \begin{aligned}&\delta _t^+A_xA_y{\mathbf {u}}^n \cdot A_tA_xA_y\varvec{\mu }^n= -\left( A_t A_xA_y\varvec{\mu }^n\right) ^T\cdot \varvec{M}({\overline{\Theta }}^{n,\star })\cdot A_t A_xA_y\varvec{\mu }^n +{\mathbf {g}}(A_xA_y{\mathbf {u}}^{n,\star })\cdot \\ {}&A_tA_xA_y\varvec{\mu }^n, A_tA_xA_y\varvec{\mu }^n \cdot \delta _t^+A_xA_y{\mathbf {u}}^n = A_tA_xA_y\varvec{k}^n\cdot \delta _t^+A_xA_y{\mathbf {u}}^n - {\overline{\nabla }}_h\cdot A_t\varvec{H}^n\\ {}&\cdot \delta _t^+A_xA_y{\mathbf {u}}^n. \end{aligned} \right. \end{aligned}$$

(6.32)

Combing the two equations, we have

$$\begin{aligned} \begin{aligned}&\left( \begin{array}{l} \frac{1}{2}A_t A_xA_yV^n\cdot A_xA_yP^{n,\star } \\ \frac{A_t A_xA_yu^n}{\tau _v} \end{array} \right) \cdot \delta _t^+ A_xA_y{\mathbf {u}}^n- {\overline{\nabla }}_h\cdot A_t \varvec{H}^n\cdot \delta _t^+A_xA_y{\mathbf {u}}^n\\&= -\left( A_t A_xA_y\varvec{\mu }^n\right) ^T\cdot \varvec{M}({\overline{\Theta }}^{n,\star })\cdot A_t A_xA_y\varvec{\mu }^n +{\mathbf {g}}(A_xA_y{\mathbf {u}}^{n,\star })\cdot A_tA_xA_y\varvec{\mu }^n, \end{aligned} \end{aligned}$$

(6.33)

with the aid of Lemma 4.1, the term $- {\overline{\nabla }}_h\cdot A_t\varvec{H}^n\cdot \delta _t^+A_xA_y{\mathbf {u}}^n$ can be transformed into

$$\begin{aligned} - {\overline{\nabla }}_h\cdot A_t\varvec{H}^n\cdot \delta _t^+A_xA_y{\mathbf {u}}^n =\,&-\nabla _h^{[1]}\cdot \left( \delta _t^+{\mathbf {u}}^n \cdot A_t\varvec{H}^n \right) \nonumber \\&+\left( \begin{matrix} \epsilon ^2 A_t A_xA_yU^n\cdot A_xA_y\varvec{R}^{n,\star } \\ D\cdot {\overline{\nabla }}_hA_t u^n \end{matrix} \right) \cdot \delta _t^+{\overline{\nabla }}_h{\mathbf {u}}^n. \end{aligned}$$

(6.34)

Then, we have

$$\begin{aligned} \begin{aligned}&\epsilon ^2 A_t A_xA_yU^n\cdot A_xA_y\varvec{R}^{n,\star }\cdot \delta _t^+{\overline{\nabla }}_h\phi ^n+\frac{1}{2}A_t A_xA_yV^n \cdot A_xA_yP^{n,\star }\cdot \delta _t^+ A_xA_y\phi ^n\\&\qquad +\frac{A_t A_xA_yu^n}{\tau _v}\delta _t^+ A_xA_y u^n\\&\qquad +(\delta _t^+{\overline{\nabla }}_h u^n)^T\cdot D\cdot {\overline{\nabla }}_hA_t u^n - \nabla _h^{[1]}\cdot \left( A_t \varvec{H}^n\cdot \delta _t^+{\mathbf {u}}^n \right) \\&\qquad + \left( A_t A_xA_y\varvec{\mu }^n\right) ^T\cdot \varvec{M}({\overline{\Theta }}^{n,\star })\cdot A_t A_xA_y\varvec{\mu }^n\\&\quad ={\mathbf {g}}(A_xA_y{\mathbf {u}}^{n,\star })\cdot A_t A_xA_y\varvec{\mu }^n \end{aligned} \end{aligned}$$

(6.35)

Inserting the last two equations of (4.39) into (4.38) arrives at

$$\begin{aligned} \begin{aligned} \delta _t^+ E^n&= \epsilon ^2 A_t A_xA_yU^n\cdot A_xA_y\varvec{R}^{n,\star }\cdot \delta _t^+{\overline{\nabla }}_h\phi ^n+\frac{1}{2}A_t A_xA_yV^n \cdot A_xA_yP^{n,\star }\cdot \delta _t^+ A_xA_y\phi ^n\\&\quad +\frac{A_t A_xA_yu^n}{\tau _v}\delta _t^+ A_xA_y u^n+(\delta _t^+{\overline{\nabla }}_h u^n)^T\cdot D\cdot {\overline{\nabla }}_hA_t u^n. \end{aligned} \end{aligned}$$

(6.36)

Inserting (6.36) into (6.35), we complete the proof.