Abstract
This paper is devoted to the definition and computation of the tensor complete orthgonal decomposition of a third-order tensor called t-URV decompositions. We first give the definition for the t-URV decomposition of a third-order tensor and derive a deterministic algorithm for computing the t-URV. We then present a randomized algorithm to approximate t-URV, named compressed randomized t-URV (cort-URV). Note that t-URV and cort-URV are extensions of URV and compressed randomized URV from the matrix case to the tensor case, respectively. We also establish the deterministic and average-case error bounds for this algorithm. Finally, we illustrate the effectiveness of the proposed algorithm via several numerical examples, and we apply cort-URV to compress the data tensors from some image and video databases.










Similar content being viewed by others
Data Availability
All datasets are publicly available.
Notes
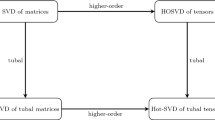
A permutation tensor \({\mathcal {P}}\in \mathbb {R}^{I_2\times I_2\times I_3}\) is a tensor whose entries consist of only zeros and 1’s, and for which \({\mathcal {P}}^\top *{\mathcal {P}}={\mathcal {P}}*{\mathcal {P}}^\top ={\mathcal {J}}_{I_2I_2I_3}\).
The Yale Face Database is at http://vision.ucsd.edu/~iskwak/ExtYaleDatabase/ExtYaleB.html.
The video dataset is at http://trace.eas.asu.edu/yuv/.
The video dataset is at http://trace.eas.asu.edu/yuv/.
References
Ailon, N., Chazelle, B.: The fast Johnson-Lindenstrauss transform and approximate nearest neighbors. SIAM J. Comput. 39, 302–322 (2009)
Battaglino, C., Ballard, G., Kolda, T.G.: A practical randomized CP tensor decomposition. SIAM J. Matrix Anal. Appl. 39, 876–901 (2018)
Biagioni, D., Beylkin, D.J., Beylkin, G.: Randomized interpolative decomposition of separated representations. J. Comput. Phys. 281, 116–134 (2015)
Boutsidis, C., Gittens, A.: Improved matrix algorithms via the subsampled randomized Hadamard transform. SIAM J. Matrix Anal. Appl. 34, 1301–1340 (2013)
Boutsidis, C., Woodruff, D.: Optimal CUR matrix decompositions. SIAM J. Comput. 46, 543–589 (2017)
Candès, E.J., Li, X., Ma, Y., Wright, J.: Robust principal component analysis? J. ACM (JACM) 58, 1–37 (2011)
Candès, E.J., Recht, B.: Exact matrix completion via convex optimization. Found. Comput. Math. 9, 717–772 (2009)
Carroll, J.D., Chang, J.: Analysis of individual differences in multidimensional scaling via an \(n\)-way generalization of “Eckart-Young’’ decomposition. Psychometrika 35, 283–319 (1970)
Chandrasekaran, S., Ipsen, I.: On rank revealing QR factorizations. SIAM J. Matrix Anal. Appl. 15, 592–622 (1994)
Che, M., Wei, Y.: Randomized algorithms for the approximations of Tucker and the tensor train decompositions. Adv. Comput. Math. 45, 395–428 (2019)
Che, M., Wei, Y., Yan, H.: The computation for low multilinear rank approximations of tensors via power scheme and random projection. SIAM J. Matrix Anal. Appl. 41, 605–636 (2020)
Che, M., Wei, Y., Yan, H.: Randomized algorithms for the low multilinear rank approximations of tensors. J. Comput. Appl. Math. 390, 113380 (2021)
Che, M., Wei, Y., Yan, H.: Randomized algorithms for the computation of multilinear rank-(\(\mu _1,\mu _2,\mu _3\)) approximations. J. Global Optim. (2022). https://doi.org/10.1007/s10898-022-01182-8
Chen, Y., Wang, S., Zhou, Y.: Tensor nuclear norm-based low-rank approximation with total variation regularization. IEEE J. Sel. Top. Signal Processing 12, 1364–1377 (2018)
Cichocki, A., Lee, N., Oseledets, I.V., Phan, A.H., Zhao, Q., Mandic, D.P.: Tensor networks for dimensionality reduction and large-scale optimization: Part 1 low-rank tensor decompositions. Foundations and Trends in Machine. Learning 9, 249–429 (2016)
Cichocki, A., Lee, N., Oseledets, I.V., Phan, A.H., Zhao, Q., Mandic, D.P.: Tensor networks for dimensionality reduction and large-scale optimization: Part 2 applications and future perspectives. Foundations and Trends in Machine. Learning 9, 431–673 (2017)
Clarkson, K.L., Woodruff, D.P.: Low-rank approximation and regression in input sparsity time. J. ACM (JACM) 63, 1–45 (2017)
De Lathauwer, L., De Moor, B., Vandewalle, J.: A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 21, 1253–1278 (2000)
Drineas, P., Mahoney, M., Muthukrishnan, S.: Relative-error CUR matrix decompositions. SIAM J. Matrix Anal. Appl. 30, 844–881 (2008)
Drineas, P., Mahoney, M.W.: RandNLA: randomized numerical linear algebra. Commun. ACM 59, 80–90 (2016)
Eckart, C., Young, G.: The approximation of one matrix by another of lower rank. Psychometrika 1, 211–218 (1936)
Erichson, N.B., Manohar, K., Brunton, S.L., Kutz, J.N.: Randomized CP tensor decomposition, Machine Learning. Sci. Technol. 1(2), 025012 (2020)
Fierro, R.D., Hansen, P.C., Hansen, P.S.K.: UTV tools: Matlab templates for rank-revealing UTV decompositions. Numerical Algorithms 20, 165–194 (1999)
Georghiades, A.S., Belhumeur, P.N., Kriegman, D.: From few to many: illumination cone models for face recognition under variable lighting and pose. IEEE Trans. Pattern Anal. Mach. Intell. 23, 643–660 (2001)
Golub, G., Van Loan, C.: Matrix Computations, Johns Hopkins University Press, Baltimore, MD, fourth ed. (2013)
Gopal, A., Martinsson, P.: The powerURV algorithm for computing rank-revealing full factorizations, arXiv preprint arXiv: 1812.06007v1 (2018)
Grasedyck, L., Kressner, D., Tobler, C.: A literature survery of low-rank tensor approximation techniques. GAMM-Mitteilungen 36(1), 53–78 (2013)
Grasedyck, L.: Hierarchical singular value decomposition of tensors. SIAM J. Matrix Anal. Appl. 31, 2029–2054 (2010)
Gu, M.: Subspace iteration randomization and singular value problems. SIAM J. Sci. Comput. 37, A1139–A1173 (2015)
Halko, N., Martinsson, P.-G., Tropp, J.: Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 53, 217–288 (2011)
Hao, N., Kilmer, M.E., Braman, K.S., Hoover, R.C.: Facial recognition using Tensor-Tensor decompositions. SIAM J. Imag. Sci. 6, 437–463 (2013)
Huber, B., Schneider, R., Wolf, S.: A randomized tensor train singular value decomposition. In: Boche, H., Caire, G., Calderbank, R., März, M., Kutyniok, G., Mathar, R. (eds.) Compressed Sensing and its Applications, pp. 261–290. Applied and Numerical Harmonic Analysis. Birkhäuser, Cham (2017)
Jiang, T.-X., Ng, M.K., Zhao, X.-L., Huang, T.-Z.: Framelet representation of tensor nuclear norm for third-order tensor completion. IEEE Trans. Image Process. 29, 7233–7244 (2020)
Kaloorazi, M., De Lamare, R.: Compressed randomized UTV decompositions for low-rank matrix approximations. IEEE J. Selected Top. Signal Processing 12, 1155–1169 (2018)
Kaloorazi, M., De Lamare, R.: Subspace-orbit randomized decomposition for low-rank matrix approximations. IEEE Trans. Signal Process. 66, 4409–4424 (2018)
Kaloorazi, M.F., Chen, J.: Projection-based QLP algorithm for efficiently computing low-rank approximation of matrices. IEEE Trans. Signal Process. 69, 2218–2232 (2021)
Kernfeld, E., Kilmer, M., Aeron, S.: Tensor-tensor products with invertible linear transforms. Linear Algebra Appl. 485, 545–570 (2015)
Kilmer, M., Martin, C.: Factorization strategies for third-order tensors. Linear Algebra Appl. 435, 641–658 (2011)
Kilmer, M.E., Braman, K.S., Hao, N., Hoover, R.C.: Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 34, 148–172 (2013)
Kilmer, M. E., Horesh, L., Avron, H., Newman, E.: Tensor-tensor algebra for optimal representation and compression of multiway data, Proceedings of the National Academy of Sciences 118(28), e2015851118 (2021)
Kolda, T., Bader, B.: Tensor decompositions and applications. SIAM Rev. 51, 455–500 (2009)
Kong, H., Lu, C., Lin, Z.: Tensor q-rank: New data dependent definition of tensor rank. Mach. Learn. 110, 1867–1900 (2021)
Kressner, D., Perisa, L.: Recompression of hadamard products of tensors in tucker format. SIAM J. Sci. Comput. 39, A1879–A1902 (2017)
Lu, C.: Tensor-Tensor Product Toolbox, Carnegie Mellon University, June 2018. https://github.com/canyilu/tproduct
Lu, C., Feng, J., Chen, Y., Liu, W., Lin, Z., Yan, S.: Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization. In: Proceedings of the IEEE conference on computer vision and pattern recognition 5249–5257 (2016)
Lu, C., Feng, J., Chen, Y., Liu, W., Lin, Z., Yan, S.: Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Analysis Mach. Intell. 42, 925–938 (2020)
Mahoney, M.W.: Randomized algorithms for matrices and data. Foundations and Trends in Machine. Learning 3, 123–224 (2011)
Malik, O.A., Becker, S.: Fast randomized matrix and tensor interpolative decomposition using CountSketch. Adv. Comput. Math. 46, 76 (2020)
Martin, C.D., Shafer, R., Larue, B.: An order-\(p\) tensor factorization with applications in imaging. SIAM J. Sci. Comput. 35, A474–A490 (2013)
Martin, D., Fowlkes, C., Tal, D., Malik, J.: A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proc. 8th Int’l Conf. Computer Vision, 2, 416–423 (2001)
Martinsson, P., Quintanaorti, G., Heavner, N.: randUTV: A blocked randomized algorithm for computing a rank-revealing UTV factorization. ACM Trans. Math. Software 45, 1–26 (2019)
Meng, X., Mahoney, M. W.: Low-distortion subspace embeddings in input-sparsity time and applications to robust linear regression. In: Proceedings of the forty-fifth annual ACM symposium on Theory of computing 91–100 (2013)
Miao, Y., Wei, Y., Qi, L.: Generalized tensor function via the tensor singular value decomposition based on the T-product. Linear Algebra Appl. 590, 258–303 (2020)
Miao, Y., Wei, Y., Qi, L.: T-Jordan canonical form and T-Drazin inverse based on the T-product, Communications on. Appl. Math. Comput. 3, 201–220 (2021)
Minster, R., Saibaba, A.K., Kilmer, M.: Randomized algorithms for low-rank tensor decompositions in the Tucker format. SIAM J. Math. Data Sci. 2, 189–215 (2020)
Musco, C., Musco, C.: Randomized block krylov methods for stronger and faster approximate singular value decomposition. Adv. Neural. Inf. Process. Syst. 28, 1396–1404 (2015)
Oseledets, I.V.: Tensor-Train decomposition. SIAM J. Sci. Comput. 33, 2295–2317 (2011)
Semerci, O., Hao, N., Kilmer, M., Miller, E.: Tensor-based formulation and nuclear norm regularization for multienergy computed tomography. IEEE Trans. Image Process. 23, 1678–1693 (2014)
Song, G., Ng, M.K., Zhang, X.: Robust tensor completion using transformed tensor singular value decomposition. Numer. Linear Algebra Appl. 27, e2299 (2020)
Stewart, G.: An updating algorithm for suspace tracking. IEEE Trans. Signal Process. 40, 1535–1541 (1992)
Stewart, G.: Updating a rank-revealing ULV decomposition. SIAM J. Matrix Anal. Appl. 14, 494–499 (1993)
Stewart, G.: The QLP approximation to the singular value decomposition. SIAM J. Sci. Comput. 20, 1336–1348 (1999)
Sun, Y., Guo, Y., Luo, C., Tropp, J., Udell, M.: Low-rank Tucker decomposition of a tensor from streaming data. SIAM J. Math. Data Sci 2, 1123–1150 (2020)
Tarzanagh, D.A., Michailidis, G.: Fast randomized algorithms for t-product based tensor operations and decompositions with applications to imaging data. SIAM J. Imag. Sci. 11, 2629–2664 (2018)
Tucker, L.R.: Some mathematical notes on three-mode factor analysis. Psychometrika 31, 279–311 (1966)
Vervliet, N., De Lathauwer, L.: A randomized block sampling approach to canonical polyadic decomposition of large-scale tensors. IEEE J. Sel. Top. Signal Process. 10, 284–295 (2016)
Wang, S., Zhang, Z.: Improving CUR matrix decomposition and the Nyström approximation via adaptive sampling. J. Mach. Learn. Res. 14, 2729–2769 (2013)
Woodruff, D.P.: Sketching as a tool for numerical linear algebra. Found. Trends Theor. Comput. Sci. 10, 1–157 (2014)
Woolfe, F., Liberty, E., Rokhlin, V., Tygert, M.: A fast randomized algorithm for the approximation of matrices. Appl. Comput. Harmon. Anal. 25, 335–366 (2008)
Zhang, J., Saibaba, A.K., Kilmer, M.E., Aeron, S.: A randomized tensor singular value decomposition based on the t-product. Numer. Linear Algebra Appl. 25, 1–24 (2018)
Zhang, Z., Aeron, S.: Exact tensor completion using t-SVD. IEEE Trans. Signal Process. 65, 1511–1526 (2017)
Zhang, Z., Ely, G., Aeron, S., Hao, N., Kilmer, M.: Novel methods for multilinear data completion and de-noising based on tensor-SVD. In: Proceedings of the IEEE conference on computer vision and pattern recognition 3842–3849 (2014)
Zhou, G., Cichocki, A., Xie, S.: Decomposition of big tensors with low multilinear rank, arXiv preprint arXiv:1412.1885v1 (2014)
Acknowledgements
The first author would like to thank Dr. Weiyang Ding of Fudan University for some results about the t-SVD. The authors like to thank Editor-in-Chief Chi-Wang Shu and two anonymous reviewers for very helpful comments.
Funding
M. Che is supported by the National Natural Science Foundation of China under Grant 11901471. Y. Wei is supported by the National Natural Science Foundation of China under Grant 11771099, Innovation Program of Shanghai Municipal Education Commission and Shanghai Municipal Science and Technology Commission under Grant 22WZ2501900.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
M. Che: This author is supported by the National Natural Science Foundation of China under Grant 11901471.
Y. Wei: This author is supported by the National Natural Science Foundation of China under Grant 11771099, Innovation Program of Shanghai Municipal Education Commission and and Shanghai Municipal Science and Technology Commission under Grant 22WZ2501900.
Proofs
Proofs
1.1 The Proof of Theorem 3.1
Let \({\mathbf {F}}_{I_3}\in \mathbb {C}^{I_3\times I_3}\) be the normalized discrete Fourier transform matrix. Then \(({\mathbf {F}}_{I_3}\otimes {\mathbf {I}}_{I_1})\cdot \mathrm{bcirc}({\mathcal {A}})\cdot ({\mathbf {F}}_{I_3}^{\mathrm{H}}\otimes {\mathbf {I}}_{I_2})=\mathrm{bdiag}({\mathbf {D}}_1,\dots ,{\mathbf {D}}_{I_3})\), where \({\mathbf {D}}_k\in \mathbb {C}^{I_1\times I_2}\). Hence for each k, we compute the URV decomposition of \({\mathbf {D}}_k\) as \({\mathbf {D}}_k={\mathbf {U}}_k\cdot {\mathbf {R}}_k\cdot {\mathbf {V}}_k^\top \). Then
When we apply \({\mathbf {F}}_{I_3}^{\mathrm{H}}\otimes {\mathbf {I}}_{I_1}\) to the left-hand side and \({\mathbf {F}}_{I_3}\otimes {\mathbf {I}}_{I_2}\) to the right-hand side of (A.1), then
are block circulant matrices. We define \(\mathrm{unfold}({\mathcal {U}})\), \(\mathrm{unfold}({\mathcal {R}})\) and \(\mathrm{unfold}({\mathcal {V}})\) as the first block columns of each of block circulant matrices in (A.2), respectively. By folding these results, we give a decomposition of the form \({\mathcal {U}}*{\mathcal {R}}*{\mathcal {V}}^{\top }\).
Now we prove that \({\mathcal {U}}\in \mathbb {R}^{I_1\times I_1\times I_3}\) and \({\mathcal {V}}\in \mathbb {R}^{I_2\times I_2\times I_3}\) are orthogonal. Note that
By the definition of t-product, \({\mathcal {U}}\) is orthogonal. We can also prove that \({\mathcal {V}}\) is orthogonal.
1.2 The Proof of Theorem 4.1
From Corollary 2.1, the left-hand side of (4.2) can be rewritten as
By Theorem 2.2, the result in (4.2) immediatedly follows.
We have
where the first inequality holds for Theorem 2.2 and the second inequality holds due to (4.2).
Now we prove (4.3). From Corollary 2.1, we have
which implies that
Here \(\widehat{{\mathcal {A}}}_K={ fft}({\mathcal {A}}_K,[],3)\) and \(\widehat{{\mathcal {A}}}_{(:,:,k),K}\) is the best rank-K approximation of \(\widehat{{\mathcal {A}}}_{(:,:,k)}\). Writing \({\mathcal {A}}={\mathcal {A}}_K+{\mathcal {A}}-{\mathcal {A}}_K\), using the fact that for given three nonegative numbers \(a_i\in \mathbb {R}\) with \(i=1,2,3\), \(a_1^2\le a_2^2+a_3^2\) implies that \(a_1\le a_2+a_3\), and applying the triangle inequality gives (4.3).
1.3 The Proof of Theorem 4.3
Note that \(\widehat{{\mathcal {Q}}}_1\in \mathbb {C}^{I_1\times L\times I_3}\) and \(\widehat{{\mathcal {Q}}}_2\in \mathbb {C}^{I_2\times L\times I_3}\) are, respectively, defined as \(\widehat{{\mathcal {Q}}}_1(:,:,k)={\mathbf {Q}}_{1k}\) and \(\widehat{{\mathcal {Q}}}_2(:,:,k)={\mathbf {Q}}_{2k}\) with all k, where \({\mathbf {Q}}_{1k}\) and \({\mathbf {Q}}_{2k}\) are obtained from Step 9 of Algorithm 4.1.
Let \({\mathcal {Q}}_1={ ifft}(\widehat{{\mathcal {Q}}}_1,[],3)\) and \({\mathcal {Q}}_2={ ifft}(\widehat{{\mathcal {Q}}}_2,[],3)\). From Theorem 4.2, we have
By Corollary 2.1, we have
where \(\widehat{{\mathcal {A}}}_{K,(:,:,k)}\), \(\widehat{{\mathcal {Q}}}_{1,(:,:,k)}\) and \(\widehat{{\mathcal {Q}}}_{2,(:,:,k)}\) are the k-th frontal slices of \(\widehat{{\mathcal {A}}}_{K}\), \(\widehat{{\mathcal {Q}}}_{1}\) and \(\widehat{{\mathcal {Q}}}_{2}\), respectively.
For all k, let
From the proof of Theorem 5 in [35], for all k, we have
According to the definitions of \({\mathbf {W}}_k\) and \({\mathbf {D}}_k\), we have
Let \(f(x)=\frac{x}{\sqrt{1+x^2}}\) with \(x>0\). Then the derivative function of f(x) is \(f'(x)=\frac{1}{(1+x^2)^{3/2}},\) which is always larger than 0 for all \(x>0\). Substituting (A.6) into (A.5) and combining the property of f(x) imply this theorem.
Remark A.1
In the proof, we also use the fact: for given \((I_3+1)\) nonegative numbers \(a_k\in \mathbb {R}\) with \(k=1,2,\dots ,I_3\), when \(a_1^2\le \frac{1}{I_3}( a_2^2+a_3^2+\dots +a_{I_3+1}^2)\), then \(a_1\le \frac{1}{\sqrt{I_3}}( a_2+a_3+\dots +a_{I_3+1})\).
1.4 The Proof of Theorem 4.4
For all k, the matrices \(\varvec{\Omega }_{1k}\) and \(\varvec{\Omega }_{2k}\) are given in (4.4). Since the matrix \({\mathbf {G}}\) is a standard Gaussian matrix, then the entries of \(\varvec{\Omega }_{1k}\) and \(\varvec{\Omega }_{2k}\) are i.i.d. standard Gaussian variables. Hence, we first take expections over \(\varvec{\Omega }_{2k}\) and next over \(\varvec{\Omega }_{1k}\). By invoking Theorem 4.3, and Propositions 2.1 and 2.2, we have
which implies the result.
Rights and permissions
About this article
Cite this article
Che, M., Wei, Y. An Efficient Algorithm for Computing the Approximate t-URV and its Applications. J Sci Comput 92, 93 (2022). https://doi.org/10.1007/s10915-022-01956-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-022-01956-y
Keywords
- Tensor-tensor product
- t-URV
- Approximate t-URV
- Compressed randomized t-URV
- Deterministic error
- Probabilistic error