Abstract
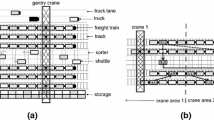
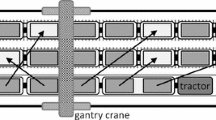
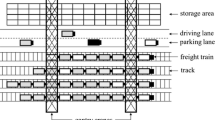
An efficient container transfer in railway yards is an important matter to increase the attraction of rail-bound freight transport. Therefore, the scheduling of gantry cranes transferring containers between freight trains and trucks or among trains received a lot of attention in the recent years. This paper contributes to this stream of research by investigating the computational complexity of crane scheduling in these yards. Scheduling the transfer of a given set of containers by a single crane equals the (asymmetric) traveling salesman problem in its path-version. In railway yards, however, all container positions are located along parallel lines, i.e., tracks, and we face special distance metrics, so that only specially structured problem instances arise. We classify important problem settings by differentiating the transshipment direction, parking policy, and distance metric. This way, we derive problem variants being solvable to optimality in polynomial time, whereas other cases are shown to be NP-hard.























Similar content being viewed by others
References
Alicke, K. (2002). Modeling and optimization of the intermodal terminal mega hub. OR Spectrum, 24, 1–17.
Atallah, M. J., & Kosaraju, S. R. (1988). Efficient solutions to some transportation problems with applications to minimizing robot arm travel. SIAM Journal on Computing, 17, 849–869.
Bagchia, T. B., Guptap, J. N. D., & Sriskandarajah, C. (2006). A review of TSP based approaches for flowshop scheduling. European Journal of Operational Research, 169, 816–854.
Boysen, N., & Fliedner, M. (2010). Determining crane areas in intermodal transshipment yards: The yard partition problem. European Journal of Operational Research, 204, 336–342.
Boysen, N., Fliedner, M., Jaehn, F., & Pesch, E. (2013). A survey on container processing in railway yards. Transportation Science, 47, 312–329.
Boysen, N., Fliedner, M., & Kellner, M. (2010). Determining fixed crane areas in rail–rail transshipment yards. Transportation Research Part E: Logistics, 46, 1005–1016.
Boysen, N., Jaehn, F., & Pesch, E. (2011). Scheduling freight trains in rail–rail transshipment yards. Transportation Science, 45, 199–211.
Boysen, N., Scholl, J., & Stephan, K. (2017). When road trains supply freight trains: Scheduling the container loading process by gantry crane between multi-trailer trucks and freight trains. OR Spectrum, 39, 137–164.
Boysen, N., & Stephan, K. (2016). A survey on single crane scheduling in automated storage/retrieval systems. European Journal of Operational Research, 254, 691–704.
Burkard, R. E., van Deineko, V. G., van der Dal, R., Veen, J. A. A., & Woeginger, G. J. (1998). Well-solvable special cases of the traveling salesman problem: A survey. SIAM Review, 40, 496–546.
Charikar, M., & Raghavachari, B. (1998). The finite capacity dial-a-ride problem. In Proceedings of the 39th annual symposium foundations of computer science 1998 (pp. 458–467).
Cordeau, J. F., & Laporte, G. (2007). The dial-a-ride problem: Models and algorithms. Annals of Operations Research, 153, 29–46.
Dantzig, G., Fulkerson, R., & Johnson, S. (1954). Solution of a large-scale travelling-salesman problem. Journal of the Operations Research Society of America, 2, 393–410.
de Paepe, W. E., Lenstra, J. K., Sgall, J., Sitters, R. A., & Stougie, L. (2004). Computer-aided complexity classification of dial-a-ride problems. INFORMS Journal on Computing, 16, 120–132.
Froyland, G., Koch, T., Megow, N., Duane, E., & Wren, H. (2008). Optimizing the landside operation of a container terminal. OR Spectrum, 30, 53–75.
Garey, M. R., & Johnson, D. S. (1979). Computers and intractability: A guide to the theory of NP-completeness. New York: Freeman.
Gilmore, P. C., & Gomory, R. E. (1964). Sequencing a one state-variable machine: A solvable case of the traveling salesman problem. Operations Research, 12, 655–679.
Gonzalez, J. A., Ponce, E., Mataix, C., & Carrasco, J. (2008). The automatic generation of transhipment plans for a train–train terminal: Application to the Spanish–French border. Transportation Planning and Technology, 31, 545–567.
Kellner, M., & Boysen, N. (2015). RMG vs. DRMG: An evaluation of different crane configurations in intermodal transshipment yards. EURO Journal on Transportation and Logistics, 4, 355–377.
Kellner, M., Boysen, N., & Fliedner, M. (2012). How to park freight trains on rail–rail transshipment yards: The train location problem. OR Spectrum, 34, 535–561.
Kim, B.-I., Heragu, S. S., Graves, R. J., & Onge, A. S. (2003). Clustering-based order-picking sequence algorithm for an automated warehouse. International Journal of Production Research, 41, 3445–3460.
Lee, H. F., & Schaefer, S. K. (1997). Sequencing methods for automated storage and retrieval systems with dedicated storage. Computers and Industrial Engineering, 32, 351–362.
Miller, C. E., Tucker, A. W., & Zemlin, R. A. (1960). Integer programming formulation of travelling salesman problems. Journal of the Association for Computing Machinery, 7, 326–329.
Oda, Y., & Ota, K. (2001). Algorithmic aspects of pyramidal tours with restricted jump-backs. Interdisciplinary Information Sciences, 7, 123–133.
Ratliff, H. D., & Rosenthal, A. S. (1983). Order-picking in a rectangular warehouse: A solvable case of the traveling salesman problem. Operations Research, 31, 507–521.
Roodbergen, K. J., & De Koster, R. (2001). Routing order pickers in a warehouse with a middle aisle. European Journal of Operational Research, 133, 32–43.
Rote, G. (1992). The \(N\)-line traveling salesman problem. Networks, 22, 91–108.
Schaefer, T. J. (1978). The complexity of satisfiability problems. In Proceedings of the tenth annual ACM symposium on Theory of computing (pp. 216–226). New York: ACM Press.
Van den Berg, J. P., & Gademann, A. J. R. M. (1999). Optimal routing in an automated storage/retrieval system with dedicated storage. IIE Transactions, 31, 407–415.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: NP-completeness of 1-in-3-Sat without negated literals even if all variables occur two or three times
1-in-3-Sat Given a set V of variables and a collection C of clauses over V, such that each clause \(c \in C\) has \(|c| = 3\). Is there a truth assignment for V, such that each clause \(c \in C\) has exactly one true literal?
1-in-3-Sat is NP-complete in the strong sense in general (Schaefer 1978; Garey and Johnson 1979) and remains so even if no clause contains a negated literal (Garey and Johnson 1979). In a recent paper, Boysen and Stephan (2016) show that 1-in-3-Sat without negated literals is NP-complete in the strong sense even if no variable occurs in more than three clauses.
Lemma 9.1
1-in-3-Sat without negated literals is strongly NP-complete even even if no variable occurs in more than three clauses.
Proof
(Lemma 9.1) See Boysen and Stephan (2016). \(\square \)
Lemma 9.2
1-in-3-Sat without negated literals is strongly NP-complete even if all variables occur two or three times.
Proof
(Lemma 9.2) To construct a 1-in-3-Sat instance without negated literals with all variables occurring at least twice we just have to double all clauses that contain variables occurring only once in the clause set. Afterward we can apply the transformation of Boysen and Stephan (2016) for proving Lemma 9.1 to reduce the number of occurrences for all variables to at most three. Note that this transformation preserves the property of all variables occurring at least twice. \(\square \)
Appendix 2: Equivalence of the Manhattan and maximum metric under \(45^{\circ }\)-rotation
This section provides an example for the equivalence of the Manhattan and maximum metric under \(45^{\circ }\)-rotation, which is elaborated by Garey and Johnson (1979) when treating the geometric TSP. The Manhattan distances between the points A to E depicted in Fig. 24a exactly equal the maximum distances within Fig. 24c. Thereby, the new grid of tracks and slots (Fig. 24c) becomes some more close-meshed (the distances between the tracks and slots decrease to \(1/\sqrt{2}\) of the original ones), which requires a rescaling of the tracks and slots.
Rights and permissions
About this article
Cite this article
Stephan, K., Boysen, N. Crane scheduling in railway yards: an analysis of computational complexity. J Sched 20, 507–526 (2017). https://doi.org/10.1007/s10951-017-0520-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10951-017-0520-6