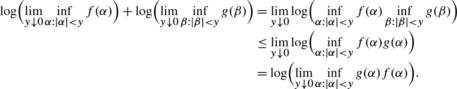Skip to main content
SpringerLink
Log in

The Transformation Method for Continuous-Time Markov Decision Processes

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

In this paper, we show that a discounted continuous-time Markov decision process in Borel spaces with randomized history-dependent policies, arbitrarily unbounded transition rates and a non-negative reward rate is equivalent to a discrete-time Markov decision process. Based on a completely new proof, which does not involve Kolmogorov’s forward equation, it is shown that the value function for both models is given by the minimal non-negative solution to the same Bellman equation. A verifiable necessary and sufficient condition for the finiteness of this value function is given, which induces a new condition for the non-explosion of the underlying controlled process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Notes

  1. Here we measurably extend ϕ ∗ with ϕ ∗(x ∞):=a ∞.

  2. So if \(\textbf{V}(\cdot)\) is bounded, there exists a deterministic stationary ϵ-optimal policy.

  3. This simple fact follows from the observation of

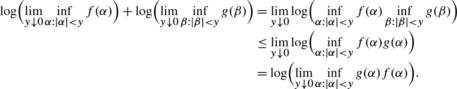
References

  1. Guo, X., Hernández-Lerma, O., Prieto-Rumeau, T.: A survey of recent results on continuous-time Markov decision processes. Top 14, 177–257 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  2. Guo, X., Piunovskiy, A.: Discounted continuous-time Markov decision processes with constraints: unbounded transition and loss rates. Math. Oper. Res. 36, 105–132 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  3. Piunovskiy, A., Zhang, Y.: Discounted continuous-time Markov decision processes with unbounded rates: the dynamic programming approach. arXiv:1103.0134v1 [math.OC] (2011)

  4. Piunovskiy, A., Zhang, Y.: Discounted continuous-time Markov decision processes with unbounded rates: the convex analytic approach. SIAM J. Control Optim. 49, 2032–2061 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  5. Feinberg, E.: Continuous time discounted jump Markov decision processes: a discrete-event approach. Math. Oper. Res. 29, 492–524 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  6. Piunovskiy, A.: Discounted continuous time Markov decision processes: the convex analytic approach. In: Proc. of the 16th Triennial IFAC World Congress, Praha (2005)

    Google Scholar 

  7. Puterman, M.: Markov Decision Processes: Discrete Stochastic Dynamic Programming. Wiley, New York (1994)

    MATH  Google Scholar 

  8. Serfozo, F.: An equivalence between continuous and discrete time Markov decision processes. Oper. Res. 27, 616–620 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  9. Hu, Q.: CTMDP and its relationship with DTMDP. Chin. Sci. Bull. 35, 710–714 (1990)

    Google Scholar 

  10. Zhang, Y.: From absorbing discrete-time Markov decision processes to discounted continuous-time Markov decision processes in Borel spaces with unbounded rates: the generalized uniformization technique. Submitted

  11. Guo, X., Hernández-Lerma, O.: Continuous-Time Markov Decision Processes: Theory and Applications. Springer, Heidelberg (2009)

    Book  MATH  Google Scholar 

  12. Guo, X., Zhu, W.: Denumerable-state continuous-time Markov decision processes with unbounded transition and reward rates under the discounted criterion. J. Appl. Probab. 39, 233–250 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Guo, X.: Continuous-time Markov decision processes with discounted rewards: the case of Polish spaces. Math. Oper. Res. 32, 73–87 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kitaev, M.: Semi-Markov and jump Markov controlled models: average cost criterion. Theory Probab. Appl. 30, 272–288 (1986)

    Article  MATH  Google Scholar 

  15. Jacod, J.: Multivariate point processes: predictable projection, Radon-Nykodym derivatives, representation of martingales. Z. Wahrscheinlichkeitstheorie Verw. Gebite. 31, 235–253 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  16. Kitaev, M., Rykov, V.: Controlled Queueing Systems. CRC Press, Boca Raton (1995)

    MATH  Google Scholar 

  17. Piunovskiy, A.: A controlled jump discounted model with constraints. Theory Probab. Appl. 42, 51–71 (1998)

    Article  MathSciNet  Google Scholar 

  18. Bertsekas, D., Shreve, S.: Stochastic Optimal Control. Academic Press, New York (1978)

    MATH  Google Scholar 

  19. Hernández-Lerma, O., Lasserre, J.: Discrete-Time Markov Control Processes. Springer, New York (1996)

    Google Scholar 

  20. Blackwell, D., Freedman, D., Orkin, M.: The optimal reward operator in dynamic programming. Ann. Probab. 2, 926–941 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  21. Piunovskiy, A.: Optimal control of random sequences in problems with constraints. Kluwer, Dordrecht (1997)

    Book  MATH  Google Scholar 

  22. Feinberg, E.: Total reward criteria. In: Feinberg, E., Shwartz, A. (eds.) Handbook of Markov Decision Processes: Methods and Applications, pp. 173–207. Kluwer, Boston (2002)

    Chapter  Google Scholar 

  23. Schäl, M., Sudderth, W.: Statiolnary policies and Markov policies in Borel dynamic programming. Probab. Theory Relat. Fields 74, 91–111 (1987)

    Article  Google Scholar 

  24. Hernández-Lerma, O., Lasserre, J.: Further Topics on Discrete-Time Markov Control Processes. Springer, New York (1999)

    MATH  Google Scholar 

  25. van der Val, J.: Stochastic Dynamic Programming: Successive Approximations and Nearly Optimal Strategies for Markov Decision Processes and Markov Games. Math. Centre. Tracts, vol. 139, Mathematish Centrum, Amsterdam (1981)

    Google Scholar 

  26. Anderson, W.: Continuous-Time Markov Chains: An Application-Oriented Approach. Springer, New York (1991)

    Book  Google Scholar 

  27. Yan, H. Zhang: J. and Guo, X.: Continuous-time Markov decision processes with unbounded transition and discounted-reward rates. Stoch. Anal. Appl. 26, 209–231 (2003)

    Article  Google Scholar 

  28. Avrachenkov, K., Piunovskiy, A., Zhang, Y.: Asymptotic fluid optimality and efficiency of tracking policy for bandwidth-sharing networks. J. Appl. Probab. 48, 90–113 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  29. Piunovskiy, A., Zhang, Y.: Accuracy of fluid approximations to controlled birth-and-death processes: absorbing case. Math. Methods Oper. Res. 73, 159–187 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  30. Shwartz, A.: Death and discounting. IEEE Trans. Autom. Control 46, 644–647 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  31. Hinderer, K.: Foundations of Non-stationary Dynamic Programming with Discrete Time Parameter. Springer, Berlin (1970)

    MATH  Google Scholar 

Download references

Acknowledgements

We are grateful to the editors and one of the anonymous referees for their valuable comments. We also thank Mr. Daniel S. Morrison for his advice regarding the English presentation of this article.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, University of Liverpool, Liverpool, L69 7ZL, UK

    Alexey Piunovskiy & Yi Zhang

Authors
  1. Alexey Piunovskiy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yi Zhang.

Additional information

Communicated by M. Pontani.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Piunovskiy, A., Zhang, Y. The Transformation Method for Continuous-Time Markov Decision Processes. J Optim Theory Appl 154, 691–712 (2012). https://doi.org/10.1007/s10957-012-0015-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-012-0015-8

Keywords

Search

Navigation