Performance Limit of Broadband Beamformer Designs in Space and Frequency

Abstract

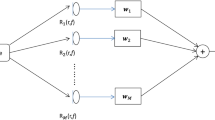
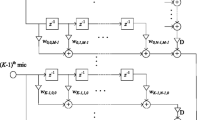
The design problem of broadband beamformers is to choose the coefficients of the filters such that the difference between the actual spatial directivity pattern and a desired spatial directivity pattern is minimized. There are many factors which can influence the performance of the design. The prominent factors include the filter length and the number of microphones. In the literature, the condition in fitting a desired spatial directivity pattern totally has not been studied properly. We show here that it is essential to use both the filter length and the number of sensors in reducing the cost function to zero, subject to some conditions on the desired response. These conditions are investigated and developed. Numerical examples are used to verify the derived conditions and at the same time to present some optimal beamformer designs.

Appendix

1.1 Proof of Lemma 3.1

Proof

Since the basis $\{1, \cos k\omega ,\sin k\omega ,\;\; k=1,\ldots ,\infty \}$ are orthogonal and complete in $[-\pi ,\pi ]$, and $u(\omega )$ and $v(\omega )$ are periodic, continuous, absolute integrable, and both right-hand and left-hand derivatives exist, then, their Fourier series are given by

$$\begin{aligned} u(\omega )= a_{0}+\sum _{k=1}^{+\infty }a_{k}\cos k\omega ,\quad v(\omega )= \sum _{k=1}^{+\infty }b_{k}\sin k\omega . \end{aligned}$$

Define $x_{k}$ by

$$\begin{aligned} x_{k}:=a_{0},\;\; x_{k}:=\left\{ \begin{array}{l@{\quad }l} (a_{k}-b_{k})/2, &{} \text {if }k>0\\ (a_{-k}+b_{-k})/2, &{} \text {if }k<0 \end{array}\right. \end{aligned}$$

Then, we have

$$\begin{aligned} \sum _{k=-\infty }^{+\infty }x_{k}e^{-j k\omega }&= a_{0}+\sum _{k=1}^{+\infty }x_{-k}e^{-j (-k)\omega } +\sum _{k=1}^{\infty }x_{k}e^{-j k\omega } \\&= a_{0}+\sum _{k=1}^{+\infty }\frac{a_{k}+b_{k}}{2}(\cos k\omega +j \sin k\omega )\\&+\sum _{k=1}^{+\infty }\frac{a_{k}-b_{k}}{2}(\cos k\omega -j \sin k\omega ) \\&= a_{0}+\sum _{k=1}^{+\infty }a_{k}\cos k\omega +j\sum _{k=1}^{+\infty }b_{k}\sin k\omega =u(\omega )+jv(\omega ). \end{aligned}$$

This completes the proof. $\square$

1.2 Proof of Lemma 4.1

Proof

Since the basis $\{1, \cos k\omega ,\sin k\omega ,\;\; k=1,\ldots ,\infty \}$ are orthogonal and complete in $[-\pi ,\pi ]$, and $u(\omega )$ and $v(\omega )$ are periodic, continuous, absolute integrable, and both right-hand and left-hand derivatives exist, then, their Fourier series are given by

$$\begin{aligned} \begin{aligned}&u(\omega )= a_{0}+\sum _{k=1}^{+\infty }a_{k}\cos k\omega + \sum _{k=1}^{+\infty }b_{k}\sin k\omega , \\&v(\omega )= c_{0}+\sum _{k=1}^{+\infty }c_{k}\cos k\omega + \sum _{k=1}^{+\infty }d_{k}\sin k\omega . \end{aligned} \end{aligned}$$

Define $x_{k}$ and $y_{k}$ by

$$\begin{aligned} \begin{aligned}&x_{0}:=a_{0},\;\;y_{0}:=c_{0},\\&x_{k}:=\left\{ \begin{array}{l@{\quad }l} (a_{k}-d_{k})/2, &{} \text {if }k>0\\ (a_{-k}+d_{-k})/2, &{} \text {if }k<0 \end{array}\right. \\&y_{k}:=\left\{ \begin{array}{l@{\quad }l} (c_{k}+b_{k})/2, &{} \text {if }k>0\\ (c_{-k}-b_{-k})/2, &{} \text {if }k<0 \end{array}\right. \end{aligned} \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{aligned} \sum _{k=-\infty }^{+\infty }(x_{k}\!+\!jy_{k})e^{-j k\omega }&=(x_{0}\!+\!jy_{0}) \!+\!\sum _{k=1}^{+\infty }(x_{-k}\!+\!jy_{-k})e^{-j (-k)\omega } \!+\!\!\sum _{k=1}^{\infty }(x_{k}\!+\!jy_{k})e^{-j k\omega } \\&=(a_{0}+jc_{0})\!+\!\sum _{k=1}^{+\infty } \left( \!\frac{a_{k}\!+\!d_{k}}{2}\!+\!j\frac{c_{k}\!-\!b_{k}}{2}\!\right) (\cos k\omega +j \sin k\omega ) \\& +\sum _{k=1}^{+\infty }\left( \frac{a_{k}-d_{k}}{2}+j\frac{c_{k}+b_{k}}{2}\right) (\cos k\omega -j \sin k\omega ) \\&= a_{0}+\sum _{k=1}^{+\infty }a_{k}\cos k\omega + \sum _{k=1}^{+\infty }b_{k}\sin k\omega \\& +j\left( c_{0}+\sum _{k=1}^{+\infty }c_{k}\cos k\omega + \sum _{k=1}^{+\infty }d_{k}\sin k\omega \right) \\&=u(\omega )+jv(\omega ). \end{aligned} \end{aligned}$$

This completes the proof. $\square$

1.3 Proof of Theorem 4.1

Proof

For any $f\in [0,f_\mathrm{{s}}/2]$, take a transform $\varphi =\nu (f)\phi$. Denote $\mathcal {A}^{0}_{k}(f,\phi )$ and $R(f,\phi )$ by $\bar{\mathcal {A}}_{k}(f,\varphi )$ and $\bar{R}(f,\varphi )$, respectively, with $\phi$ being replaced by $\varphi$. Then, it follows from (24) that $\bar{\mathcal {A}}_{k}(f,\varphi )$ is given by

$$\begin{aligned} \bar{\mathcal {A}}_{k}(f,\varphi )=e^{-j2\pi k\varphi }= e^{-j2\pi k\nu (f)\phi }. \end{aligned}$$

(a)

Then, $\bar{\mathcal {A}}_{k}(f,\varphi )\in \left\{ e^{-j2\pi k\varphi }, k=-\infty ,\ldots ,+\infty \right\}$.

For the definition of $\bar{R}(f,\varphi )$, note that the transform $\phi \rightarrow \varphi$ is a bijection and maps $[-1,1]$ to $[-\nu (f),\nu (f)]\subset [-1/2,1/2]$, if $f>0$. We define $\bar{R}(f,\varphi )=R(f,\phi /\nu (f))$, $\forall \varphi \in [-\nu (f),\nu (f)]$. If $f=0$, then $\nu (f)=0$ and the transform $\phi \rightarrow \varphi$ maps $[-1,1]$ to a point $0$. Note that $R(0,\phi )$ is a real constant number, and then define $\bar{R}(0,0)=R(0,0)$. Hence, $\bar{R}(f,\varphi )$ is well defined.

The definition domain of $\bar{\mathcal {A}}_{k}(f,\varphi )$ and $\bar{R}(f,\varphi )$ is $\Omega =\{(f,\varphi ):f\in [0,f_\mathrm{{s}}/2],\varphi \in [-\nu (f),\nu (f)]\}$. Since the real part and the imaginary part of $R(f,\phi )$ are continuous, absolute integrable, and both right-hand and left-hand derivatives exist in $[0,f_\mathrm{{s}}/2]\times [-1,1]$, then the real part and the imaginary part of $\bar{R}(f,\varphi )$ are also continuous, absolute integrable, and both right-hand and left-hand derivatives exist in $\Omega$.

Then, the problem (30) is equivalent to find a sequence of complex functions $\{\mathcal {X}^{0}_{k}(f)\in \Gamma _{0},k=-\infty ,\ldots ,+\infty \}$, such that

$$\begin{aligned} \bar{R}(f,\varphi )=\sum _{k=-\infty }^{+\infty } \mathcal {X}^{0}_{k}(f)\bar{\mathcal {A}}_{k}(f,\varphi ) =\sum _{k=-\infty }^{+\infty } \mathcal {X}^{0}_{k}(f)e^{-j2\pi k\varphi }, \quad \forall (f,\varphi )\in \Omega . \end{aligned}$$

(b)

To prove (b), we extend the definition of $\bar{R}(f,\varphi )$ from $\Omega$ to $[0,f_\mathrm{{s}}/2]\times \mathbb {R}$. The extended definition of $\bar{G}_\mathrm{{d}}(f,\varphi ,\eta ,\bar{\eta })$ should keep some conditions:

• (i) $\bar{R}(0,\varphi )$ are real constant numbers.

• (ii) The real part and the imaginary part of $\bar{R}(f_\mathrm{{s}}/2,\varphi )$ are even and odd, respectively.

• (iii) For each $f\in [0,f_\mathrm{{s}}/2]$, $\bar{R}(f,\varphi )$ is periodic with period $1$.

• (iv) The real part and the imaginary part of $\bar{R}(f,\varphi )$ are continuous, absolute integrable, and both right-hand and left-hand derivatives exist.

It remains to extend the definition domain from $\Omega$ to $[0,f_\mathrm{{s}}/2]\times [-1/2,1/2]$ with the terminal condition $\bar{R}(f,-1/2)=\bar{R}(f,1/2)$. Then, the function will be periodic with period $1$.

Note that if $r=c/f_\mathrm{{s}}$, $\nu (f_\mathrm{{s}}/2)=1$. It is not necessary to extend the definition of $\bar{R}(f,\varphi )$ when $f=f_\mathrm{{s}}/2$, since $\bar{R}(f_\mathrm{{s}}/2,x)=R(f_\mathrm{{s}}/2,x/2)$, $\forall x\in [-1,1]$. It follows from the conditions (A2)–(A4) in Theorem 4.1 that the conditions (ii)–(iv) are satisfied in the case of $f=f_\mathrm{{s}}/2$.

There are many kinds of methods for the extension. A simple method is the linear interpolation. For each $f\in [0,f_\mathrm{{s}}/2]$, we extend the definition of $\bar{R}(f,\varphi )$ as

$$\begin{aligned} \bar{R}(f,\varphi )=&\left\{ \begin{array}{l@{\quad }l} \frac{1-\nu (f)+\varphi }{1-2\nu (f)}\bar{R}(f,-\nu (f)) +\frac{-\nu (f)-\varphi }{1-2\nu (f)}\bar{R}(f,\nu (f)), &{} \varphi \in [-1/2,-\nu (f)] \\ \frac{-\nu (f)+\varphi }{1-2\nu (f)}\bar{R}(f,-\nu (f)) +\frac{1-\nu (f)-\varphi }{1-2\nu (f)}\bar{R}(f,\nu (f)), &{} \varphi \in [\nu (f),1/2] \end{array}\right. \nonumber \\ =&\left\{ \begin{array}{l@{\quad }l} \frac{1-\nu (f)+\varphi }{1-2\nu (f)}R(f,-1) +\frac{-\nu (f)-\varphi }{1-2\nu (f)}R(f,1), &{} \varphi \in [-1/2,-\nu (f)] \\ \frac{-\nu (f)+\varphi }{1-2\nu (f)}R(f,-1) +\frac{1-\nu (f)-\varphi }{1-2\nu (f)}R(f,1), &{} \varphi \in [\nu (f),1/2] \end{array}\right. \end{aligned}$$

(c)

Then, by this interpolation, it can be verified directly that the conditions (i)-(iv) are satisfied.

By Lemma (4.1), for each $f\in [0,f_\mathrm{{s}}/2]$, there exists a sequence of $\{\mathcal {X}^{0}_{k}(f)=x_{k}(f)+jy_{k}(f):k=-\infty ,\ldots ,+\infty \}$ such that the equality (b) holds in $[0,f_\mathrm{{s}}/2]\times [-1/2,1/2]$. Hence, it also holds in the subset $\Omega$.

It remains to verify that $\mathcal {X}^{0}_{k}(f)\in \Gamma _{0}$, $\forall k=-\infty ,\ldots ,+\infty$. Since the coefficients exist, they can be computed directly by

$$\begin{aligned} \mathcal {X}^{0}_{k}(f)=\int _{-1/2}^{1/2}\bar{R}(f,\varphi )e^{j2\pi k\varphi }\mathrm{{d}}\varphi ,\quad \forall k=-\infty ,\ldots ,+\infty . \end{aligned}$$

(d)

Then, we verify that $\mathcal {X}^{0}_{k}(f)\in \Gamma _{0}$. From (i), $\bar{R}(0,\varphi )$ is a real constant number. Suppose that the constant is denoted by $\alpha$. Then, we have

$$\begin{aligned} \mathcal {X}^{0}_{k}(0)=\int _{-1/2}^{1/2}\alpha (\cos 2\pi k\varphi +j\sin 2\pi k\varphi ) \mathrm{{d}}\varphi =\int _{-1/2}^{1/2}\alpha \cos 2\pi k\varphi \mathrm{{d}}\varphi . \end{aligned}$$

Hence, $\mathcal {X}^{0}_{k}(0)$ is a real number.

From (ii), the real part and the imaginary part of $\bar{R}(f_\mathrm{{s}}/2,\varphi )$ are even and odd, respectively. Suppose that the real part and the imaginary part of $\bar{R}(f_\mathrm{{s}}/2,\varphi )$ are denoted by $\alpha (\varphi )$ and $\beta (\varphi )$. Then, we have

$$\begin{aligned} \mathcal {X}^{0}_{k}(f_\mathrm{{s}}/2)=\int _{-1/2}^{1/2} (\alpha (\varphi )+j\beta (\varphi ))(\cos 2\pi k\varphi +j\sin 2\pi k\varphi ) \mathrm{{d}}\varphi . \end{aligned}$$

(e)

The imaginary part of (e) is computed by

$$\begin{aligned} \mathcal {X}^{0}_{k}(f_\mathrm{{s}}/2)&= \int _{-1/2}^{1/2} (\alpha (\varphi )\sin 2\pi k\varphi +\beta (\varphi )\cos 2\pi k\varphi ) \mathrm{{d}}\varphi \\&= \int _{-1/2}^{0} (\alpha (\varphi )\sin 2\pi k\varphi +\beta (\varphi )\cos 2\pi k\varphi ) \mathrm{{d}}\varphi \\&\quad + \int _{0}^{1/2} (\alpha (\varphi )\sin 2\pi k\varphi +\beta (\varphi )\cos 2\pi k\varphi ) \mathrm{{d}}\varphi \\&= \int _{0}^{1/2} (\alpha (-\varphi ')\sin 2\pi k(-\varphi ')+\beta (-\varphi ')\cos 2\pi k(-\varphi ')) \mathrm{{d}}\varphi ' \\&\quad +\int _{0}^{1/2} (\alpha (\varphi )\sin 2\pi k\varphi +\beta (\varphi )\cos 2\pi k\varphi ) \mathrm{{d}}\varphi \\&= 0. \end{aligned}$$

Hence, $\mathcal {X}^{0}_{k}(f_\mathrm{{s}}/2)$ is a real number.

Since both the real part and the imaginary part of $\bar{R}(f,\varphi )$ are continuous, absolute integrable, and their right-hand and left-hand derivatives exist, if follows from the equation (d) that the real part and the imaginary part of $\mathcal {X}^{0}_{k}(f)$ are continuous, absolute integrable, and their right-hand and left-hand derivatives exist.

Thus, the function $\mathcal {X}^{0}_{k}(f_\mathrm{{s}}/2)$, which is given in (d), belonging to $\Gamma _{0}$. Then, equation (30) is true. This completes the proof. $\square$