A Two-on-One Linear Pursuit–Evasion Game with Bounded Controls

Abstract

A linearized engagement with two pursuers versus a single evader is considered, in which the adversaries’ controls are bounded and have first-order dynamics and the pursuers’ intercept times are equal. Wishing to formulate the engagement as a zero-sum differential game, a suitable cost function is proposed and validated, and the resulting optimization problem and its solution are presented. Construction and analysis of the game space is shown, and the players’ closed-form optimal controls are derived for the case of two “strong” pursuers. The results are compared to those of a 1-on-1 engagement with a “strong” pursuer, and it is shown that the addition of a second pursuer enlarges the capture zone and introduces a new singular zone to the game space, in which the pursuers can guarantee equal misses, regardless of the evader’s actions. Additionally, it is concluded that in the regular zones the closed-form optimal pursuit strategies are unchanged compared to two 1-on-1 engagements, whereas the optimal evasion strategy is more complex. Several simulations are performed, illustrating the adversaries’ behavior in different regions of the game space.

Appendices

Appendix A: Properties of the Agents’ Control Dynamics

Proposition A.1

$\psi (\theta \alpha )>0 \ \forall \theta>0, \ \alpha >0$

Proof

Note that $\psi (0)=0$, $\lim \limits _{\theta \rightarrow \infty }\psi (\theta \alpha )\sim \theta \alpha$, and $d\psi /d\theta =\alpha -\alpha e^{-\theta }$. Since $1-e^{-\theta }>0$ $\forall \theta >0$, it follows that $d\psi /d\theta>0 \ \forall \theta>0, \ \alpha >0$, and therefore $\psi (\theta \alpha )>0 \ \forall \theta>0, \ \alpha >0$. $\square$

Lemma A.1

Given a continuous and differentiable function $g(\theta )$ for which $g(0)=0$, $\lim \limits _{\theta \rightarrow 0^+}g(\theta )>0$ and $\lim \limits _{\theta \rightarrow \infty }g(\theta )>0$, a necessary condition for the existence of some open segment $(\theta _{s_1},\theta _{s_2}), \ 0<\theta _{s_1}<\theta _{s_2}<\infty \$ in which $g(\theta ) \le 0$ is that $dg/d\theta$ must have at least two positive roots.

Proof

Since $g(\theta )$ is continuous, $g(0)=0$ and $\lim \limits _{\theta \rightarrow \infty }g(\theta )>0$, then if $g(\theta )$ has no extrema it is necessarily a monotonically increasing function and $g(\theta )>0 \ \forall \theta >0$. Since $g(\theta )$ is continuous, $g(0)=0$ and $\lim \limits _{\theta \rightarrow 0^+}g(\theta )>0$, then if $g(\theta )$ has a single positive extremum it is necessarily a maximum point. Therefore, since $\lim \limits _{\theta \rightarrow \infty }g(\theta )>0$, then $g(\theta )>0 \ \forall \theta >0$. Hence, the existence of at least two positive extrema in $g(\theta )$ is necessary for the existence of some segment $(\theta _{s_1},\theta _{s_2}), \ 0<\theta _{s_1}<\theta _{s_2}<\infty \$ in which $g(\theta ) \le 0$. Finally, since $g(\theta )$ is differentiable, at each extremum, if such exists, $dg/d\theta =0$ and the proof is complete. $\square$

Lemma A.2

Functions of the form $h(\theta )=e^{-\theta }-\alpha e^{-\beta \theta }$ have at most one root $\forall \alpha ,\beta$.

Proof

Given such a function, its root is equal to $\theta _r=\ln (\alpha )/(\beta -1)$. Since $\ln (\cdot )$ is an injective function, if $\theta _r$ exists for given values of $\alpha$ and $\beta$ it is the sole root of $h(\theta )$. $\square$

Proposition A.2

$\frac{\mu }{\varepsilon }\psi (\theta \varepsilon )-\psi (\theta )>0 \ \forall \theta>0, \ \mu>1,\mu \varepsilon >1$

Proof

Define $f(\theta ) \triangleq \dfrac{\mu }{\varepsilon }\psi (\theta \varepsilon )-\psi (\theta )$. Note that $f(0)=0$ and $\lim \limits _{\theta \rightarrow \infty }f(\theta )\sim \theta (\mu -1)$, and that $df/d\theta =\mu -\mu e^{-\theta \varepsilon }-1+e^{-\theta }$. Note that $df/d\theta |_{\theta =0}=0$, $\lim \limits _{\theta \rightarrow 0^+}df/d\theta \sim \theta (\mu \varepsilon -1)$ and $\lim \limits _{\theta \rightarrow \infty }df/d\theta =\mu -1$, and that $d^2f/d\theta ^2=\mu \varepsilon e^{-\theta \varepsilon }-e^{-\theta }$. From Lemma A.2 it follows that $d^2f/d\theta ^2$ can have no more than one root. Therefore, since $df/d\theta$ is continuous and differentiable and since $\lim \limits _{\theta \rightarrow 0^+}df/d\theta>0 \ \forall \mu \varepsilon >1$ and $\lim \limits _{\theta \rightarrow \infty }df/d\theta >0$ $\forall \mu >1$, it follows from Lemma A.1 that $df/d\theta>0 \ \forall \theta>0 \ \forall \mu>1,\mu \varepsilon >1$. Therefore, $f(\theta )>0 \ \forall \theta >0$ $\forall \mu>1,\mu \varepsilon >1$. $\square$

Proposition A.3

$\varPsi (\theta ,\alpha )>0 \ \forall \theta>0, \ \alpha >0$

Proof

Note that $\varPsi (0,\alpha )=0$ and $\lim \limits _{\theta \rightarrow \infty }\varPsi (\theta ,\alpha )\sim (\theta \alpha )^2$, and that $d\varPsi /d\theta =\psi (\theta \alpha )$. Since from Proposition A.1 $\psi (\theta \alpha )>0 \ \forall \theta>0, \ \alpha >0$, it follows that $d\varPsi /d\theta>0 \ \forall \theta>0, \ \alpha >0$, and therefore $\varPsi (\theta ,\alpha )>0 \ \forall \theta>0, \ \alpha >0$. $\square$

Proposition A.4

$\frac{\mu }{\varepsilon }\varPsi (\theta ,\varepsilon )-\varPsi (\theta ,1) \ge 0 \ \forall \theta \ge 0, \ \mu>1,\mu \varepsilon >1$

Proof

Define $F(\theta )=\frac{\mu }{\varepsilon }\varPsi (\theta ,\varepsilon )-\varPsi (\theta ,1)$. Note that $F(0)=0$ and $\lim \limits _{\theta \rightarrow \infty }F(\theta )\sim \theta ^2(\mu -1)$, and that $dF/d\theta =\frac{\mu }{\varepsilon }\psi (\theta \varepsilon )-\psi (\theta ) \equiv f(\theta )$, where $f(\theta )$ is as defined in Proposition A.3. From Proposition A.2 it follows that $dF/d\theta>0 \ \forall \theta \ge 0, \ \mu>1,\mu \varepsilon >1$, and therefore $F(\theta ) \ge 0$ $\forall \theta \ge 0, \ \mu>1,\mu \varepsilon >1$. $\square$

Appendix B: Properties of the Evader’s Open-Loop Strategy

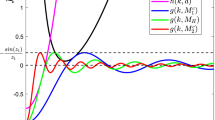
In order to determine whether the proposed product cost function is viable for the present game, we examine the behavior of the adversaries under the obtained open-loop strategies. The open-loop evasion strategy obtained in (25) using the proposed cost function can be rearranged as follows

$$\begin{aligned} u_E^*(\theta )=\mathrm {sign}\left\{ Z_{2}(0)\right\} \cdot \mathrm {sign}\left\{ |Z_{1}(0)|+\mathrm {sign}\left\{ Z_{1}(0) \cdot Z_{2}(0)\right\} \cdot |Z_{2}(0)|\right\} . \end{aligned}$$

(38)

In order to determine the evader’s performance, we examine the following cases:

Case 1 $\mathrm {sign}\left\{ Z_{1}(0)\right\} =\mathrm {sign}\left\{ Z_{2}(0)\right\}$

In this case $\mathrm {sign}\left\{ Z_{1}(0) \cdot Z_{2}(0)\right\} =1$. Therefore, $u_E^*(\theta )=\mathrm {sign}\left\{ Z_{2}(0)\right\} =\mathrm {sign}\left\{ Z_{1}(0)\right\}$.

Case 2 $\mathrm {sign}\left\{ Z_{1}(0)\right\} \ne \mathrm {sign}\left\{ Z_{2}(0)\right\}$

In this case $\mathrm {sign}\left\{ Z_{1}(0) \cdot Z_{2}(0)\right\} =-1$. Therefore,

$$\begin{aligned} u_E^*(\theta )=\mathrm {sign}\left\{ Z_{2}(0)\right\} \cdot \mathrm {sign}\left\{ |Z_{1}(0)|-|Z_{2}(0)|\right\} . \end{aligned}$$

• Case 2.1 $|Z_{1}(0)|>|Z_{2}(0)|$

  In this case $u_E^*(\theta )=\mathrm {sign}\left\{ Z_{2}(0)\right\}$.

• Case 2.2 $|Z_{1}(0)|<|Z_{2}(0)|$

  In this case $u_E^*(\theta )=-\mathrm {sign}\left\{ Z_{2}(0)\right\} =\mathrm {sign}\left\{ Z_{1}(0)\right\}$.

• Case 2.3 $|Z_{1}(0)|=|Z_{2}(0)|$

  In this case $u_E^*(\theta )=0$ $\Rightarrow$ Singular.

Hence, we deduce that the evader behaves as expected: evade the most threatening pursuer. In the interesting case of $Z_{1}(0)=-Z_{2}(0)$, if we consider $Z_{1}(0)$ and $Z_{2}(0)$ to actually be predicted values of the normalized misses, then it may in fact make sense for the evader not to apply any control (as opposed to applying any admissible control, which is equally optimal for singular solutions), since its only hope of enlarging the misses is to wait for at least one of the pursuers to diverge from its optimal strategy. Should such a divergence occur, $Z_{1}(0)=-Z_{2}(0)$ would no longer hold and the evader would strive to once again equalize the absolute values of the misses, which would now be greater.

Appendix C: Closed-Form Controls Derivation

Recall the open-loop controls given in (25)

$$\begin{aligned} \begin{aligned} u_{P_i}^*(\theta )&=\mathrm {sign}\left\{ Z_i(0)\right\} , \quad i \in N\\ u_E^*(\theta )&=\mathrm {sign}\left\{ Z_{1}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{2}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} . \end{aligned} \end{aligned}$$

From (27) we have in general along regular trajectories for $i,j\in N,\ i \ne j$

$$\begin{aligned} \begin{aligned} Z_{i}(\theta )&=Z_{i}(0)+\mathrm {sign}\left\{ Z_{i}(0)\right\} \cdot \dfrac{\mu _i}{\varepsilon _i}\varPsi (\theta ,\varepsilon _i) \\&\qquad -\mathrm {sign}\left\{ Z_{1}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{2}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} \cdot \varPsi (\theta ,1). \end{aligned} \end{aligned}$$

(39)

Alternatively,

$$\begin{aligned} \begin{aligned} Z_{i}(\theta )&=\mathrm {sign}\left\{ Z_{i}(0)\right\} \cdot \left[ {\begin{matrix}|Z_{i}(0)|+\dfrac{\mu _i}{\varepsilon _i}\varPsi (\theta ,\varepsilon _i)-\mathrm {sign}\left\{ Z_{j}(0)\right\} \\ \cdot \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} \cdot \varPsi (\theta ,1)\end{matrix}}\right] . \end{aligned} \end{aligned}$$

(40)

Regardless of the values of $Z_1(0)$ and $Z_2(0)$, we know from Proposition A.4 that $\frac{\mu _i}{\varepsilon _i}\varPsi (\theta ,\varepsilon _i)-\mathrm {sign}\left\{ Z_{j}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} \cdot \varPsi (\theta ,1)>0$. Therefore,

$$\begin{aligned} \mathrm {sign}\left\{ |Z_{i}(0)|+\frac{\mu _i}{\varepsilon _i}\varPsi (\theta ,\varepsilon _i)-\mathrm {sign}\left\{ Z_{j}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} \cdot \varPsi (\theta ,1)\right\} =1. \end{aligned}$$

Hence we conclude that on regular trajectories

$$\begin{aligned} \mathrm {sign}\{Z_i(0)\}=\mathrm {sign}\{Z_i(\theta )\}. \end{aligned}$$

(41)

We now turn our attention to the expression $\mathrm {sign}\{Z_1(0)+Z_2(0)\}$ in $u_E^*(\theta )$. Consider the following cases:

Case 1 $\mathrm {sign}\left\{ Z_{1}(0)\right\} =\mathrm {sign}\left\{ Z_{2}(0)\right\}$

In this case

$$\begin{aligned} \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} =\mathrm {sign}\left\{ Z_{1}(0)\right\} =\mathrm {sign}\left\{ Z_{2}(0)\right\} . \end{aligned}$$

(42)

From (41) we know that

$$\begin{aligned} \begin{aligned} \mathrm {sign}\left\{ Z_{1}(0)\right\}&=\mathrm {sign}\left\{ Z_{1}(\theta )\right\} \\ \mathrm {sign}\left\{ Z_{2}(0)\right\}&=\mathrm {sign}\left\{ Z_{2}(\theta )\right\} . \end{aligned} \end{aligned}$$

Therefore, since $\mathrm {sign}\left\{ Z_{1}(0)\right\} =\mathrm {sign}\left\{ Z_{2}(0)\right\}$,

$$\begin{aligned} \mathrm {sign}\left\{ Z_{1}(\theta )\right\} =\mathrm {sign}\left\{ Z_{2}(\theta )\right\} =\mathrm {sign}\left\{ Z_{1}(\theta )+Z_{2}(\theta )\right\} . \end{aligned}$$

Substituting this along with (41) in (42) yields

$$\begin{aligned} \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} =\mathrm {sign}\left\{ Z_{1}(\theta )+Z_{2}(\theta )\right\} . \end{aligned}$$

(43)

Case 2 $\mathrm {sign}\left\{ Z_{1}(0)\right\} \ne \mathrm {sign}\left\{ Z_{2}(0)\right\}$

From (39) we obtain after some algebra

$$\begin{aligned} \begin{aligned} \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} \cdot \left[ \left| Z_{1}(0)+Z_{2}(0)\right| -\mathrm {sign}\left\{ Z_{1}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{2}(0)\right\} \cdot 2\varPsi (\theta ,1)\right] \\ =\left[ Z_{1}(\theta )+Z_{2}(\theta )\right] -\mathrm {sign}\left\{ Z_{1}(0)\right\} \cdot \frac{\mu _1}{\varepsilon _1}\varPsi (\theta ,\varepsilon _1)-\mathrm {sign}\left\{ Z_{2}(0)\right\} \cdot \frac{\mu _2}{\varepsilon _2}\varPsi (\theta ,\varepsilon _2). \end{aligned} \end{aligned}$$

(44)

In this case $\mathrm {sign}\left\{ Z_{1}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{2}(0)\right\} =-1$ and therefore, following Proposition A.3, $\left| Z_{1}(0)+Z_{2}(0)\right| -\mathrm {sign}\left\{ Z_{1}(0)\right\} \cdot \mathrm {sign}\left\{ Z_{2}(0)\right\} \cdot 2\varPsi (\theta ,1)>0$. Hence from (44) we deduce that

$$\begin{aligned} \mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} =\mathrm {sign}\left\{ {\begin{matrix}\left[ Z_{1}(\theta )+Z_{2}(\theta )\right] -\mathrm {sign}\left\{ Z_{1}(0)\right\} \cdot \frac{\mu _1}{\varepsilon _1}\varPsi (\theta ,\varepsilon _1)\\ -\mathrm {sign}\left\{ Z_{2}(0)\right\} \cdot \frac{\mu _2}{\varepsilon _2}\varPsi (\theta ,\varepsilon _2) \end{matrix}}\right\} . \end{aligned}$$

Substituting (41)in the above yields

$$\begin{aligned}&\mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} =\mathrm {sign}\left\{ {\begin{matrix}\left[ Z_{1}(\theta )+Z_{2}(\theta )\right] -\mathrm {sign}\left\{ Z_{1}(\theta )\right\} \cdot \frac{\mu _1}{\varepsilon _1}\varPsi (\theta ,\varepsilon _1)\\ -\mathrm {sign}\left\{ Z_{2}(\theta )\right\} \cdot \frac{\mu _2}{\varepsilon _2}\varPsi (\theta ,\varepsilon _2)\end{matrix}}\right\} .\nonumber \\ \end{aligned}$$

(45)

Equations (43) and (45) can be expressed together by a single term

$$\begin{aligned}&\mathrm {sign}\left\{ Z_{1}(0)+Z_{2}(0)\right\} \nonumber \\&\quad =\mathrm {sign}\left\{ {\begin{matrix}\left[ Z_{1}(\theta )+Z_{2}(\theta )\right] +\mathrm {sign}\left\{ Z_1(\theta ) \cdot Z_2(\theta )-|Z_1(\theta ) \cdot Z_2(\theta )|\right\} \\ \cdot \left[ \mathrm {sign}\left\{ Z_{1}(\theta )\right\} \cdot \frac{\mu _1}{\varepsilon _1}\varPsi (\theta ,\varepsilon _1)+\mathrm {sign}\left\{ Z_{2}(\theta )\right\} \cdot \frac{\mu _2}{\varepsilon _2}\varPsi (\theta ,\varepsilon _2)\right] \end{matrix}}\right\} .\qquad \end{aligned}$$

(46)

Substituting (41) together with (46) yields the following closed-form controls

$$\begin{aligned} \begin{aligned} u_{P_i}^*(\theta )&=\mathrm {sign}\left\{ Z_{i}(\theta )\right\} , \quad i \in N\\ u_E^*(\theta )&=\mathrm {sign}\left\{ Z_1(\theta )\right\} \cdot \mathrm {sign}\left\{ Z_2(\theta )\right\} \\&\quad \cdot \mathrm {sign}\left\{ {\begin{matrix}\left[ Z_{1}(\theta )+Z_{2}(\theta )\right] +\mathrm {sign}\left\{ Z_1(\theta ) \cdot Z_2(\theta )-|Z_1(\theta ) \cdot Z_2(\theta )|\right\} \\ \cdot \left[ \mathrm {sign}\left\{ Z_{1}(\theta )\right\} \cdot \frac{\mu _1}{\varepsilon _1}\varPsi (\theta ,\varepsilon _1)+\mathrm {sign}\left\{ Z_{2}(\theta )\right\} \cdot \frac{\mu _2}{\varepsilon _2}\varPsi (\theta ,\varepsilon _2)\right] \end{matrix}}\right\} . \end{aligned} \end{aligned}$$

(47)