An Efficient Approximation Technique for Solving a Class of Fractional Optimal Control Problems

Abstract

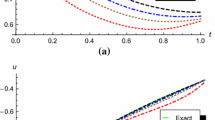
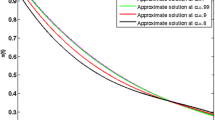
In this paper, we discuss a class of fractional optimal control problems, where the system dynamical constraint comprises a combination of classical and fractional derivatives. The necessary optimality conditions are derived and shown that the conditions are sufficient under certain assumptions. Additionally, we design a well-organized algorithm to obtain the numerical solution of the proposed problem by exercising Laguerre polynomials. The key motive associated with the present approach is to convert the concerned fractional optimal control problem to an equivalent standard quadratic programming problem with linear equality constraints. Given examples illustrate the computational technique of the method together with its efficiency and accuracy. Graphical representations are provided to analyze the performance of the state and control variables for distinct prescribed fractions.

Appendix: Singular Fractional Optimal Control Problem

We wish to address some control problems where the performance index is either linear or independent of the control function u. For example, consider the FOCP to find an optimal control u(t) that minimizes the performance index

$$\begin{aligned} J[u]=\frac{1}{2}\int _0^1 \,x^2(t)\,\mathrm{d}t \end{aligned}$$

(36)

subject to the system dynamic constraints

$$\begin{aligned} {}^{C}_0D_t^{\alpha }\,x(t)= u(t),\quad \alpha \in ]0,1[\,, \end{aligned}$$

(37)

and the initial condition $x(0)=1$. One can clearly observe that:

• The integrand of J is independent of the control function u.

• Necessary optimality conditions (Theorem 3.1) reduce to ${}_0D_t^{\alpha }x=u$, ${}_tD_1^{\alpha }\lambda =x(t)$ and $\lambda (t)=0$. The condition $\lambda (t)=0$ complicates the system to further look for some control function, and hence the control problem is termed as singular.

If $\alpha =1$, the problem stated above corresponds to the classical singular optimal control problem (see [20] and references therein). An independent investigation by researchers has to be carried out for such problems.