Granularity in Nonlinear Mixed-Integer Optimization

Abstract

We study a new technique to check the existence of feasible points for mixed-integer nonlinear optimization problems that satisfy a structural requirement called granularity. For granular optimization problems, we show how rounding the optimal points of certain purely continuous optimization problems can lead to feasible points of the original mixed-integer nonlinear problem. To this end, we generalize results for the mixed-integer linear case from Neumann et al. (Comput Optim Appl 72:309–337, 2019). We study some additional issues caused by nonlinearity and show how to overcome them by extending the standard granularity concept to an advanced version, which we call pseudo-granularity. In a computational study on instances from a standard test library, we demonstrate that pseudo-granularity can be expected in many nonlinear applications from practice, and that its explicit use can be beneficial.

Appendices

Appendix

Computation of Lipschitz Constants

In this appendix, we identify some problem classes which are suitable for the computation of the necessary Lipschitz constants in Assumption 3.1. From the mean value theorem, the Hölder inequality and the Weierstrass theorem it is well known that for fixed $x\in \mathrm{pr}_xD$ with a nonempty and compact set D(x) and a continuously differentiable (in y) function $g_i(x,\cdot )$, $i\in I$, the value

$$\begin{aligned} L^{i}_\infty (x) = \max _{y\in D(x)}\Vert \nabla _yg_i(x,y)\Vert _1 \end{aligned}$$

(10)

is a Lipschitz constant for $g_i(x,\cdot )$ on D(x) with respect to the $\ell _\infty$-norm.

To achieve uniform Lipschitz constants, let us define the ‘worst case’ Lipschitz constants among those in (10) with respect to $x\in \mathrm{pr}_xD$,

$$\begin{aligned} L^i_\infty :=\sup _{x\in \mathrm{pr}_xD}L^i_\infty (x)=\sup _{x\in \mathrm{pr}_xD}\max _{y\in D(x)}\Vert \nabla _yg_i(x,y)\Vert _1,\ i\in I. \end{aligned}$$

If we assume D to be a polytope, then the supremum is attained, and this yields

$$\begin{aligned} L^i_\infty =\max _{(x,y)\in D}\Vert \nabla _yg_i(x,y)\Vert _1,\ i\in I. \end{aligned}$$

(11)

Note that $L^i_\infty$ is preferable over the Lipschitz constant

$$\begin{aligned} {\widetilde{L}}^i_\infty :=\max _{(x,y)\in D}\Vert \nabla g_i(x,y)\Vert _1=\max _{(x,y)\in D}(\Vert \nabla _xg_i(x,y)\Vert _1+\Vert \nabla _yg_i(x,y)\Vert _1) \end{aligned}$$

for $g_i$ on D, since it promotes a larger set $T^-$. This shows that Assumption 3.1 is weaker than a general Lipschitz condition and illustrates our main motivation to require Lipschitz conditions only on the fibers $\{x\}\times D(x)$.

Example A.1

If D is a polytope and for some $i\in I$ the entries of the gradient $\nabla _y g_i$ are factorable functions, then techniques from interval arithmetic may be employed to compute $L^i_\infty$ as a guaranteed upper bound for $\max _{(x,y)\in D}\Vert \nabla _y g_i(x,y)\Vert _1$ (cf., e.g., [23, 24]). Again, since smaller Lipschitz constants lead to larger sets $T^-$, good upper bounds are beneficial for the consistency of $T^-$. $\square$

Example A.2

If for some $i\in I$ we have $g_i(x,y)=F_i(x)+\beta _i^\intercal y$, then (11) boils down to $L^{i}_\infty = \Vert \beta _i\Vert _1$. This actually explains the inclusion ‘$\supseteq$’ in (2). $\square$

Example A.3

If D is a polytope and for some $i \in I$, we have

$$\begin{aligned} g_i(x,y)= F(x) + \textstyle \frac{1}{2}y^\intercal Q_y y + y^\intercal Q_x x + \beta ^\intercal y +q, \end{aligned}$$

then

$$\begin{aligned} L^{i}_\infty \ =\ \max _{(x,y)\in D}\Vert Q_yy+ Q_{x}x + \beta \Vert _1 \end{aligned}$$

may be computed by the vertex theorem of convex maximization [25, Corollary 32.3.4] as

$$\begin{aligned} L^{i}_\infty \ =\ \max _{(x,y)\in {{\,\mathrm{vert}\,}}D}\Vert Q_yy+ Q_{x}x + \beta \Vert _1, \end{aligned}$$

where ${{\,\mathrm{vert}\,}}D$ denotes the vertex set of D. Alternatively, we may obtain $L^i_\infty$ as the optimal value of the linear program with complementarity constraints [26]

$$\begin{aligned}&\hbox {LPCC}:\qquad \max _{x,y,u,v}\,e^\intercal (u+v)\quad \text{ s.t. }\quad Q_yy+ Q_{x}x + \beta =u-v,\\&\quad \ \ u^\intercal v=0,\ \ u,v\ge 0,\ \ (x,y)\in D. \end{aligned}$$

As a third possibility, $L_\infty ^i$ can be computed as the optimal value of a mixed-integer linear optimization problem. In fact, modeling the complementarity constraint $u^\intercal v = 0$ in the above LPCC by a big-M reformulation [27, 28] results in the problem

$$\begin{aligned} \hbox {MILP}: \qquad \max _{x,y,u,v,z} e^\intercal (u+v) \quad \text{ s.t. }\quad Q_yy+ Q_{x}x + \beta&= u-v,\\ u&\le {{\,\mathrm{diag}\,}}(M_u) z, \\ v&\le {{\,\mathrm{diag}\,}}(M_v) (e- z), \\ u,v&\ge 0, \ (x,y) \in D, \ z \in \mathbb B^m, \end{aligned}$$

with $M_u,M_v \in \mathbb R^m$ large enough, where ${{\,\mathrm{diag}\,}}(M_u)$ and ${{\,\mathrm{diag}\,}}(M_v)$ denote the corresponding diagonal matrices, and e stands for the all ones vector.

Notice that, in order to obtain a tight LP relaxation, we propose not one single big-M constant, but different big-M’s for each variable $u_i$, $v_i$, $i=1,\dots , m$. We stress that good values for the entries of $M_{u}$ and $M_v$ can be computed explicitly from the problem data. Indeed, with $(q_x)_k^\intercal$ and $(q_y)_k^\intercal$ denoting row k of the Matrix $Q_x$ and $Q_y$, respectively, we may set the k’th entries of $M_u$ and $M_v$ to

$$\begin{aligned} (M_u)_k= & {} \max _{(x,y) \in D} \ (q_x)_k^\intercal x + (q_y)_k^\intercal y + \beta _k \ \text { and} \ \\ (M_v)_k= & {} - \left( \min _{(x,y) \in D} \ (q_x)_k^\intercal x + (q_y)_k^\intercal y + \beta _k \right) , \end{aligned}$$

which comes at the cost of solving 2m LPs. The validity of theses bounds for u and v immediately follows from the equality constraints $Q_yy+ Q_xx + \beta = u-v$ together with the (remodeled) complementarity constraints.

As our numerical study in Sect. 7 reveals, separable quadratic constraints $g_i$ constitute a relevant special case of this setting. Since they satisfy $Q_x = 0$, and under the explicit knowledge of box constraints for y, that is $y \in [y^\ell , y^u]$ with $y^\ell ,y^u \in \mathbb R^m$, we may compute valid (albeit possibly coarser) values for $(M_u)_k$ and $(M_v)_k$ as

$$\begin{aligned} (M_u)_k&= \max _{y \in [y^\ell ,y^u]} \sum _{j=1}^m (q_y)_{kj} y_j + \beta _k = \sum _{j: (q_y)_{kj} > 0} (q_y)_{kj}y_j^u + \sum _{j:(q_y)_{kj}<0} (q_y)_{kj} y_j^\ell + \beta _k \end{aligned}$$

(12)

$$\begin{aligned} (M_v)_k&= - \left( \min _{y \in [y^\ell ,y^u]} \sum _{j=1}^m (q_y)_{kj} y_j + \beta _k\right) \nonumber \\&= - \left( \sum _{j: (q_y)_{kj} > 0} (q_y)_{kj}y_j^\ell + \sum _{j:(q_y)_{kj}<0} (q_y)_{kj} y_j^u + \beta _k \right) , \end{aligned}$$

(13)

where $(q_y)_{kj}$ denotes the entry at row k and column j of $Q_y$. Note that these bounds are valid due to our previous construction and $\mathrm{pr}_y D\subseteq [y^\ell ,y^u]$. In our computational study, we indeed use (12) and (13) to quickly compute $M_{u}$ and $M_v$.

We remark that neither of the three above auxiliary problems for the computation of $L_\infty ^i$ is efficiently solvable in the sense that we may obtain an optimal value in polynomial time. However, our computational study reveals that the auxiliary MILP is quickly solvable for many practical applications. $\square$

Objective Value of the Generated Feasible Point

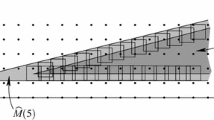
Due to rounding effects as well as due to the necessary modifications on the transition from M to ${\widetilde{T}}_\rho ^-$, the point generated by FRA-SOR can of course not be expected to be optimal for MINLP. In fact, already for a two-dimensional purely integer linear problem with two inequality constraints and the inner parallel set ${\widehat{M}}^-=T^-$, Fig. 4 illustrates that the point generated by FRA-SOR may be far from optimal. Modifying the illustrated situation by forcing the angle between the two constraints to become more acute results in examples which move the constructed point arbitrarily far away from an optimal point.

Fig. 4

Possible location of the feasible point constructed by FRA-SOR for the minimization of $y_1$

To evaluate how ‘good’ a point generated by FRA-SOR is, one may compare its objective value with the optimal value ${\widehat{v}}$ of the continuously relaxed problem $\widehat{\hbox {MINLP}}$. This yields the bounds

(14)

on the deviation of from the optimal value v of MINLP. Note that in this bound we propose to use the optimal value ${\widehat{v}}$ of f over ${\widehat{M}}$ without any enlargement constructions, rather than the optimal value of f over ${\widehat{M}}_\rho$, since this leads to a tighter bound.

In contrast to such an a-posteriori bound on the objective value , from a structural point of view one may also be interested in a-priori bounds, which only depend on the problem data of MINLP. For FRA-SOR, the derivation of such bounds is indeed possible and further discussed in [29].