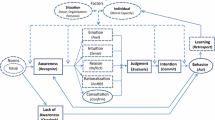
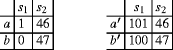Abstract
“Since today is Saturday, the grocery store is open today and will be closed tomorrow; so let’s go today”. That is an example of everyday practical reasoning—reasoning directly with the propositions that one believes but may not be fully certain of. Everyday practical reasoning is one of our most familiar kinds of decisions but, unfortunately, some foundational questions about it are largely ignored in the standard decision theory: (Q1) What are the decision rules in everyday practical reasoning that connect qualitative belief and desire to preference over acts? (Q2) What sort of logic should govern qualitative beliefs in everyday practical reasoning, and to what extent is that logic necessary for the purposes of qualitative decisions? (Q3) What kinds of qualitative decisions are always representable as results of everyday practical reasoning? (Q4) Under what circumstances do the results of everyday practical reasoning agree with the Bayesian ideal of expected utility maximization? This paper proposes a rigorous decision theory for answering all of those questions, which is developed in parallel to Savage’s (1954) foundation of expected utility maximization. In light of a new representation result, everyday practical reasoning provides a sound and complete method for a very wide class of qualitative decisions; and, to that end, qualitative beliefs must be allowed to be closed under classical logic plus a well-known nonmonotonic logic—the so-called system ℙ.
Similar content being viewed by others
Notes
To be more precise, Morris defines qualitative beliefs to be the negations of decision-theoretically null propositions.
Namely, a ∼ b iff a ≽ b ≽ a, and a ≻ b iff a ≽ b ≯̲ a.
Namely, o ≡ o′ iff o ≥ o′ ≥ o, and o > o′ iff o ≥ o′ ≱ o.
That notation is borrowed from statistics. Think of a as a random variable: proposition/event a > 3 is a shorthand for {s ∈ S a(s) > 3}.
Although the English statement of the Conditional Cliché Rule emplys the phrase ‘believes that, if A, then B’, the present work is compatible with different interpretation of that phrase. It is compatible with the interpreation that the belief of a conditional is the belief of the proposition expressed by the conditional. It is also compatible with the alternative interpretation that the belief of a conditional is a conditional belief that is irreducible to the belief of any proposition. That is why I model the concept of ‘believes that, if A, then B’ by ordered pairs of propositions.
Remark on notation: For readers familiar with nonmonotonic logic, think of Bel(A ⇒ B) as A | ∼ B. Although the latter notation is standard in nonmonotonic logic, I do not adopt it because it is usually understood to formalize “if A, normally B” while I wish to formalize “the agent believes that, if A, then B”. An alternative notation is Bel(B | A); read: the agent believes B given A. Although that notation would fit the practice in probability theory better, it reverses the order of antecedent A and consequent B that is commonly adopted in nonmonotonic logic and, hence, is awkward for stating the logical principles standardly called “left equivalence” and “right weakening”. Note that A ⇒ B is not intended to denote an element of an algebra; think of Bel( · ⇒ · ) as a binary relation between propositions.
It may appear surprising that the concept of “sure” can be reduced to conditional beliefs. But here is a heursitic argument that motivates the reduction. Argue as follows that Bel( ¬ A ⇒ ⊥ ) implies P(A) = 1. Suppose for reductio that Bel( ¬ A ⇒ ⊥ ) but P(A) < 1. So P( ¬ A) > 0 and, hence, P( ⊥ ∣ ¬ A) is defined and equal to 0. But we should never believe a conditional with zero conditional probability, so ¬ Bel( ¬ A ⇒ ⊥ ), which contradicts our supposition. So if Bel( ¬ A ⇒ ⊥ ), then P(A) = 1 (and, furthermore, P( ⊥ ∣ ¬ A) is not defined). I propose that we stipulate that the converse is also true, and obtain the biconditional: Bel( ¬ A ⇒ ⊥ ) iff P(A) = 1. I think one of the anonymous referees for his or her critical comment, which inspires this heuristic argument.
P(s) abbreviates the strictly correct notation P({s}).
Conditional probability P(B|A) is defined in the standard way as P(B ∩ A)/P (A), which exists just in case P(A) > 0.
In the following example, the maximin rule favors a over b and favors b′ over a′ , which violates (Qualitative Simplification):
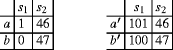
Strictly speaking, system ℙ also contains:
$$\begin{array}{@{}rcl@{}} \begin{array}{ll} {\sf Bel}(A \Rightarrow B)& \\ A~\mathrm{is~logically~equivalent~to}~C& \quad(\mathbf{Left~Equivalence}) \\ \overline{\sf Bel(\mathit{C} \Rightarrow \mathit{B})} \end{array} \end{array}$$But given the non-syntactical treatment adopted here, two propositions are logically equivalent iff they are identical. So (Left Equivalence) holds trivially.
Philosophers of science speak of hypothetico-deductivism as the view that observing a logical consequence C of a theory B provides evidence in favor of the theory. Since it would be strange to retract theory C in light of new, positive evidence B, I refer to the proposed principle as Hypothetico-Deductive Monotonicity.
The weakest nonmonotonic logics ever studied are perhaps those validated by the probability-threshold semantics; see [11], [12], and [24]. In the present terminology, that semantics can be defined as follows. For each probability-threshold t and each probability measure P over the propositions, define the following conditional belief set: Bel P, t (A ⇒ B) iff either P(B | A) ≥ t or P(A) = 0. The class of such conditional belief sets validates the minimal system, while it invalidates system ℙ (e.g., (Cautious Monotonicity), (And), and (Or)).
For another example, Gilboa and Schmeidler [10] assume infinitely many acts (for any two acts f , g and real number r ∈ (0, 1), the mixture r f + (1 − r)g is a distinct act).
See, e.g., [25] for a review on the literatue about bounded rationality.
This strategy of proving (And) is due to [7].
Why disjoint? Getting an umbrella in a rainy state is an outcome distinct from getting an umbrella in a sunny state.
I thank an anonyous referee for asking me a stimulating question to help me think it through.
In fact, they ultimately represent > L by another kind of belief representation, called possibility measures. I frame the discussion in terms of > L simply because it facilitates the comparison.
Proof. It suffices to show that Bel(a ≢ b ⇒ a > b) implies Bel(a > b ∪ a < b ⇒ a > b) and that the converse does not hold. Suppose that Bel(a ≢ b ⇒ a > b). Note that a > b ⊆ a > b ∪ a < b. So, by (Left Weakening), Bel(a ≢ b ⇒ a > b ∪ a < b). Then, by (Cautious Monotonicity), Bel(a ≢ b ∩ (a > b ∪ a < b) ⇒ a > b). Simplify the antecedent by the assumption that ≥ is transitive and reflexive, we have Bel(a > b ∪ a < b ⇒ a > b). To see that the converse does not hold, it suffices to see that, if X ⊃ Y ⊃ Z, then it is possible that Bel(Y ⇒ Z) but ¬ Bel(X ⇒ Z).
References
Adams, E. W. (1975). The logic of conditionals. Dordrecht: D. Reidel.
Brafman, M., & Tennenholtz, M. (1996). On the foundations of qualitative decision theory. In Proceedings of the 13th national conference on artificial intelligence (pp. 1291–1296). Portland: AAAI-96.
Bratman, M. (1987). Intention, plans, and practical reason. Cambridge: Harvard University Press.
Boutilier, C. (1994). Toward a logic for qualitative decision theory. In J. Doyle et al. (Eds), Proceedings of 4th international conference on principles of knowledge representation and reasoning (pp. 75–86). Bonn: KR’94.
Cohen, L. J. (1989). Belief and acceptance. Mind, 98, 367–389.
Doyle, J., & Thomason, R. (1999). Background to qualitative decision theory. AI Magazine, 20(2), 55–68.
Dubois, D., Fargier, H., Prade, H., Perny, P. (2002). Qualitative decision theory: from savage’s axioms to nonmonotonic reasoning. Journal of the ACM, 49(4), 455–495.
Ellsberg, D. (1961). Risk, ambiguity, and the savage axioms. Quarterly Journal of Economics, 75(4), 643–669.
Fantl, J., & McGrath, M. (2009). Knowledge in an uncertain world. Oxford: Oxford University Press.
Gilboa, I., & Schmeidler, D. (1989). Maxmin expected utility with non-unique prior. Journal of Mathematical Economics, 18, 141–153.
Hawthorne, J. (1996). On the logic of nonmonotonic conditionals and conditional probabilities. Journal of Philosophical Logic, 25, 185–218.
Hawthorne, J., & Makinson, D. (2007). The quantitative/qualitative watershed for rules of uncertain inference. Studia Logica, 86, 249–299.
Hawthorne, J. (2004). Knowledge ad lottery. Oxford: Oxford University Press.
Hawthorne, J., & Stanley, J. (2008). Knowledge and action. Journal of Philosophy, 105, 571–590.
Jeffrey, R. (1970). Dracula meets wolfman: acceptance vs. partial belief. In M. Swain (Ed.), Induction, acceptance, and rational belief (pp. 157-185).
Kraus, S., Lehmann, D., Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44, 167–207.
Kyburg, H. (1961). Probability and the logic of rational belief . Middletown: Wesleyan University Press.
Leitgeb, H. (2010). Reducing belief simpliciter to degrees of belief. Presentation at the opening celebration of the center for formal epistemology at Carnegie Mellon University in June.
Lin, H., & Kelly, K. T. (2012). Propositional reasoning that tracks probabilistic reasoning. Journal of Philosophical Logic, 41(6), 957–981.
Maher, P. (1993). Betting on theories. Cambridge: Cambridge University Press.
McCarthy, J. (1980). Circumscription: a form of non-monotonic reasoning. Artificial Intelligence, 13, 27–39.
Morris, S. (1996). The logic of belief and belief change: a decision theoretic approach. Journal of Economic Theory, 29(1), 1–23.
Neta, R. (2009). Treating something as a reason for action. Noûs, 23, 684–699.
Paris, J., & Simmonds, R. (2009). O is not enough. Review of Symbolic Logic, 2, 298–309.
Pingle, M. (2006). Deliberation cost as a foundation for behavoral economics. In M. Altman (Ed.), Handbook of contemporary behavioral economics: foundations and developments, (Chap. 17). New York: M.E. Sharpe.
Ross, J., & Schroeder, M. (2012). Belief, credence, and pragmatic encroachment. Philosophy and Phenomenological Research. doi:10.1111/j.1933-1592.2011.00552.x.
Savage, L. J. (1954). The foundations of statistics. New York: Wiley.
Shafer, G. (1986). Savage revisited. Statistical Science, 1, 463–485.
Shoham, Y. (1987). A semantical approach to nonmonotonic logics. In M. Ginsberg (Ed.), Readings in nonmonotonic reasoning. Los Altos: Morgan Kauffman.
Thomason, R. (2009). Logic and artificial intelligence. In E.N. Zalta (Ed.), The stanford encyclopedia of philosophy (Spring 2009 Edition). http://plato.stanford.edu/archives/spr2009/entries/logic-ai/.
Williamson, T. (2000). Knowledge and its limits. Oxford: Oxford University Press.
Acknowledgments
The author is indebted to Dubois and his colleagues’ pioneering work, without which I would not see the possibility of a foundation for everyday practical reasoning. I am also indebted to David Etlin, Kevin Kelly, Hannes Leitgeb, Olivier Roy, Vincenzo Crupi, for extensive discussions. I am also indebted to the participants of the 10th Conference on Logic and the Foundations of Game and Decision Theory (Sevilla, June 2012) and the 5th Workshop on Frontiers of Rationality and Decision (Groningen, August 2012), especially Branden Fitelson, Giacomo Bonanno, Michael Trost, Daniel Eckert, and Jan-Willem Romeijn. I am also indebted to the three anonymous referees of LOFT and the two anonymous referees of the Journal of Philosophical Logic for detailed comments. I am also indebted to Clark Glymour, Horacio Arlo-Costa, Kevin Zollman, Arthur Paul Pedersen, and Teddy Seidenfeld for comments on my earlier thoughts that lead to the present paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Proof of Theorem 1
Proof of the “If” Side Suppose that conditions 1-3 holds. Without danger of confusion, write a ≽ b to abbreviate a ≽ b a s i c b. We will use the following results:
The proof is given below, which relies on the representability of ≥ by U:
Prove (Consistency with Bayesian Preference) as follows:
(by (8))
(by (8))□
Proof of the “Only If” Side
Suppose that (Consistency with Bayesian Preference) holds. Argue as follows that ≥ is represented by U. Suppose that o 1 ≡ o 2. So o 1 ≡ o 2 = ⊤ . Since Sure( ⊤ ), it follows from the Sure Equivalence Rule that o 1 ∼ o 2. So, by (Consistency with Bayesian Preference), E U P (o 1) = E U P (o 2). It follows that U(o 1) = U(o 2). By the same argument, o 1 > o 2implies U(o 1) > U(o 2).
Argue as follows that Sure(A) iff P(A) = 1. By hypothesis, o 0 < o 1. So, by representability, U(o 0) < U(o 1). Let f be the act that maps each state s ∈ A to the worse outcome o 0, and maps the other states to the more desirable outcome o 1. Compare f to the constant act o 0. If Sure(A), then, by the Sure Equivalence Rule, f ∼ o 0, and hence, by (Consistency with Bayesian Preference), E U P (f) = E U P (o 0), which is the case only if P(A) = 1. Suppose that ¬ Sure(A). By hypothesis, Bel( ¬ A ⇒ ¬ A) (Reflexivity). It follows from the Conditional Cliché Rule that f ≻ o 0. Then, by (Consistency with Bayesian Preference), E U P (f) > E U P (o 0), which is the case only if P(A) ≠ 1.
Suppose, for reductio, that condition 3 is violated; namely, there exist propositions A, B ⊆ S such that A ⊇ B, Bel(A ⇒ B), ¬ Sure( ¬ A) (so P(A) > 0), but \(P(B|A) \le \frac {\Delta U}{\Delta U + \delta U}\). Since some outcome is better than some other outcome, δ U > 0. So \(P(B|A) \le \frac {\Delta U}{\Delta U + \delta U} < 1\). It follows that:
Then, the definition of ΔU and δ U guarantees that there exist outcomes o 0 ≤ o 1 < o 2 ≤ o 3 ∈ O such that:
Let a, b be the acts defined by the following conditions:
-
(i)
for all s ∈ A ∩ B = B, a(s) = o 2 > o 1 = b(s);
-
(ii)
for all \(s \in A \cap \overline B\), a(s) = o 0 < o 3 = b(s);
-
(iii)
for all \(s \in \overline A\), a(s) = b(s) = o 0.
Then, the upper bound in (9) guarantees that E U P (a) ≤ E U P (b). Argue as follows that a ≻ b. By the reductio hypothesis, Bel(A ⇒ B) and ¬ Sure( ¬ A). Note that A = [[a ≢ b]] and B = [[a > b]]. So, by the Conditional Cliché Rule, a ≻ b. To recap, we have that a ≻ b but E U P (a) ≤ E U P (b), which contradicts (Maximal Consistency with Bayesian Preference). □
Appendix B: Proof of Propositions 1 and 2: Decision Rules in the Elegant Form
Proof of Proposition 1
Suppose that Bel(S ⇒ [[a > b]]). Since ≥ is reflexive and transitive, [[a > b]] ⊆ [[a ≢ b]]. So, by (Right Weakening), Bel(S ⇒ [[a ≢ b]]). Since Bel(S ⇒ [[a > b]]) and Bel(S ⇒ [[a ≢ b]]), we have Bel([[a ≢ b]] ⇒ [[a > b]]) by (Cautious Monotonicity). Suppose for reductio that Bel([[S ⇒ a > b]]) and Bel([[a ≢ b]] ⇒ ∅). Note that Bel([[a ≢ b]] ⇒ ∅) implies that Bel([[a ≢ b]] ⇒ [[a ≡ b]]) by (Right Weakening), and we already have that Bel([[a ≡ b]] ⇒ [[a ≡ b]]) by (Reflexivity). So, by (Or), Bel([[a ≡ b]] ∪ [[a ≢ b]] ⇒ [[a]] ≡ [[b]]). Namely, Bel(S ⇒ [[a ≡ b]]). But Bel(S ⇒ [[a > b]]) (by hypothesis). So, by (And), Bel(S ⇒ [[a ≡ b]] ∩ [[a > b]]). But ≥ is a preorder, so Bel(S ⇒ ∅), which contradicts the assumption that Bel is consistent. □
Proof of Proposition 2
Argue that (3) + (4) implies (6) as follows. Assume the basic rules (3) + (4). Suppose that a ≽ b (and we want to show that Bel([[a ≢ b]] ⇒ [[a > b]])). Case 1: a ∼ b. Then, by (4), Bel([[a ≢ b]] ⇒ ∅). So, by (Right Weakening), Bel([[a ≢ b]] ⇒ [[a > b]]). Case 2: a ≻ b. Then, by (3), either Bel(S ⇒ [[a > b]]), or Bel([[a ≢ b]] ⇒ [[a > b]]). But the first disjunct implies the second disjunct, by Proposition 1. Hence, the second disjunct is true; namely, Bel([[a ≢ b]] ⇒ [[a > b]]). To prove the converse, suppose that Bel([[a ≢ b]] ⇒ [[a > b]]) (and we want to show that a ≽ b). Case 1: Bel([[a ≢ b]] ⇒ ∅. Then apply (4) to derive a ∼ b and, thus, a ≽ b. Case 2: ¬Bel([[a ≢ b]] ⇒ ∅). Then apply (3) to derive a ≻ b and, thus, a ≽ b.
Argue that (6) implies (3)+(4) as follows. Assume the elegant form of the basic rules (6). For the left-to-right side of (4), suppose a ∼ b. So a ≽ b and b ≽ a. Then, by (6), Bel([[a ≢ b]] ⇒ [[a > b]]) and Bel([[b ≢ a]] ⇒ [[a > b]]). The latter is equivalent to Bel([[a ≢ b]] ⇒ [[a < b]]). So, by (And), Bel([[a ≢ b]] ⇒ [[a > b]] ∩ [[a < b]]). But the conjunction [[a > b]] ∩ [[a < b]] equals ∅ , for ≥ is reflexive and transitive. So we have that Bel([[a ≢ b]] ⇒ ∅), which is the right-hand side of (4), as required. For the right-to-left side of (4), suppose that Bel([[a ≢ b]] ⇒∅). Then, by (Right Weakening), we have both Bel([[a ≢ b]] ⇒ [[a > b]]) and Bel([[a ≢ b]] ⇒ [[a < b]]). The latter is equivalent to Bel([[b ≢ a]] ⇒ [[a > b]]). So, by (6), a ≽ b and b ≽ a. Hence, a ∼ b, as required. To prove (3), note that, by definition, a ≻ b iff (i) a ≽ b and (ii) a ≁ b. By (6), the first conjunct (a ≽ b) is equivalent to Bel([[a ≢ b]] ⇒ [[a > b]]). By (4), the second conjunct (a ≁ b) is equivalent to ¬Bel([[a ≢ a]] ⇒∅). So a ≻ b iff Bel([[a ≢ b]] ⇒ [[a > b]]) and ¬Bel([[a ≢ b]] ⇒ ∅), which implies (3) by Proposition 1. □
Appendix C: Proof of Theorem 2: Sound Representation
The proof of (Reflexivity), (Dominance), and (Qualitative Simplification) is routine verification given the lemma that, for all outcomes o, o′ ∈ O, o ≥ o′ iff o ≽ o′ , which we prove as follows. Argue as follows that if o > o′ then o ≻ o′ . Suppose that o > o′ . So o > o′ = ⊤ . By (Reflexivity), Bel( ⊤ ⇒ ⊤ ), namely Bel( ⊤ ), namely Bel(o > o′ ). So, by the Cliché Rule, o ≻ o′ . Argue as follows that if o ≡ o′ then o ∼ o′ . Suppose that o ≡ o′ . So o ≡ o′ = ⊤ . By (Reflexivity), Bel( ⊥ ⇒ ⊥ ), namely Bel( ¬ ⊤ ⇒ ⊥ ), namely Sure( ⊤ ), namely Sure(o ≡ o′ ). So, by the Sure Equivalence Rule, o ∼ o′ . For the last case, argue as follows that if o ≱ o′ then o ≯̲ o′ . Suppose that o ≱ o′ . So o > o′ = ⊥ , o ≡ o′ = ⊥ , and o ≢ o′ = ⊤ . Then, o≯̲o′ follows from the hypotheses that ≽ is represented by the basic rules for everyday decision, and that Bel is consistent (i.e., ¬ Bel( ⊤ ⇒ ⊥ )).
The proof of (Transitivity) is provided below, in which we will make extensive use of system ℙ with two of its derived rules:
Proof of Transitivity
Abbreviate Bel(X ⇒ Y) as X | ∼ Y (which is the standard notation in nonmonotonic logic). Suppose that a ≽ b and b ≽ c. With the help of Proposition 2, apply the elegant form of the basic rules to a ≽ b:
Apply (Left-Right Or) to (10); then we have:
For the antecedent of (11), distribute the first disjunct into the conjunction, and we obtain:
Apply the elegant form of the basic rules to b ≽ c, and repeat the derivation from (10) to (12)—but with a R b and b R c exchanged. Then we have:
Apply (And) to (12) and (13), we have:
Verify that the consequent of the above formula entails a > c as follows: rewrite the consequent of the above formula by the identity: (A ∪ A′ ) ∩ (B ∪ B′ ) = (A ∩ B) ∪ (A ∩ B′ ) ∪ (A′ ∩ B) ∪ (A′ ∩ B′ ), so that we obtain the disjunction of four disjuncts; then it is routine to verify that each of the four disjuncts entails a > c. Then, apply (Right Weakening) to (14); we have:
Apply the De Morgan rule to the antecedent of (16); then we have:
Note that the consequent of (17) entails a ≢ c. So, apply (Hypothetico-Deductive Monotonicity) to (17); then we have:
In the antecedent of (18), the second conjunct a ≢ c entails the first conjunct, so the entire antecedent is equal to the second conjunct. Hence:
Then, apply the elegant form of the basic rules to (19), we have that a ≽ c, as required. □
Appendix D: Proof of Theorem 3: Complete Representation
Let preference relation ≽ be simplified qualitatively, i.e., satisfy axioms (Reflexivity), (Transitivity), (Dominance), and (Qualitative Simplification). The full strength of the (Regularity) condition is needless until Lemma 5. For now we only need to assume a strictly weaker condition: there exist outcomes 0, 1 ∈ O such that 0 ≺ 1. For each proposition A ⊆ S, let f A be the act defined by:
Define conditional belief set Bel as follows:
for all propositions A, B ⊆ S. Define a desirability relation ≥ over outcomes as follows:
for all outcomes o, o′ ∈ O.
Lemma 1
≥ is reflexive and transitive.
Proof
≥ is, by definition, isomorphic to the restriction of ≽ to constant acts, which satisfies (Reflexivity) and (Transitivity). □
Lemma 2
Bel is consistent
Proof
Suppose for reductio that Bel(S ⇒ ∅). Then, by definition, \(f_{S \cap \varnothing } \succeq f_{S \cap \overline {\varnothing }}\). In other words, \(f_{\varnothing } \succeq f_{S}\). So, by definition, 0 ≽ 1, which contradicts that 1 ≻ 0. □
Lemma 3
Bel satisfies (Reflexivity).
Proof
Let A be an arbitrary proposition. By (Dominance), \(f_{A} \succeq f_{\varnothing }\). In other words, \(f_{A \cap A} \succeq f_{A \cap \overline A}\). So, by definition, Bel(A ⇒ A). □
Lemma 4
Bel satisfies (Right Weakening ).
Proof
Suppose that Bel(X ⇒ A) and A ⊆ A′ . Since Bel(X ⇒ A), \(f_{X \cap A} \succeq f_{X \cap \overline {A}}\), by definition. Then, since A ⊆ A′ , it follows from (Dominance) both that f X ∩ A′ ≽ f X ∩ A and that \(f_{X \cap \overline {A}} \succeq f_{X \cap \overline {A'}}\). So we have established that \(f_{X \cap A'} \succeq f_{X \cap A} \succeq f_{X \cap \overline {A}} \succeq f_{X \cap \overline {A'}}\). Then, by (Transitivity), \(f_{X \cap A'} \succeq f_{X \cap \overline {A'}}\). Hence, by definition, Bel(X ⇒ A′ ). □
From now on, assume the full strength of (Regularity). So we have outcomes 0, 1, 2 ∈ O such that 0 ≺ 1 ≺ 2. When the antecedent of the (Qualitative Simplification) axiom holds, say that the two act-pairs in question, 〈a, b〉 and 〈a′ , b′〉 , are ordinally similar.
Lemma 5
≽ is represented by the elegant form of the basic rules with respect to ≥ and Bel; namely, for all acts a, b:
Proof
Let a, b be arbitrary acts. Define propositions N = a ≢ b (‘N’ for ‘not equally good’), B = a > b (‘B’ for ‘better’). By the definition of Bel, it suffices to prove the following equivalence:
Here are the preliminaries. Let s be an arbitrary state in S. Then:
Similarly,
Then we prove the equivalence (22) by the following cases.
-
Case 1: all outcomes in O are comparable with respect to ≽ . Then we have:
$$\begin{array}{@{}rcl@{}} a(s) \sim b(s) &\iff& a(s) \equiv b(s) \\ &\iff& s \not\in N \\ &\iff& f_{N \cap B}(s) = 0 \sim 0 = f_{N \cap \overline B}(s) \\ &\iff& f_{N \cap B}(s) \sim f_{N \cap \overline B}(s). \end{array}$$So a, b is ordinally similar to \(\left< f_{N \cap B}, f_{N \cap \overline B} \right >\) and, hence, (Qualitative Simplification) applies: a ≽ b iff \(f_{N \cap B} \succeq f_{N \cap \overline B}\). (Whenever we apply (Qualitative Simplification) in the following, verification of ordinal similarity will be omitted because it is routine).
-
Case 2: some outcomes in O are non-comparable with respect to ≽ and, hence, the second part of (Regularity) condition applies. Argue as follows that:
$$\begin{array}{@{}rcl@{}} a \succeq b &\implies& f_{N \cap B} \;\succeq\; f_{N \cap \overline B}. \end{array}$$Suppose that a ≽ b. By (Regularity), there are outcomes \(o \Bumpeq o' \Bumpeq o'' \succ o\). Define acts c, d, e as follows (the outcomes of the acts are specified with respect to the states in the following four propositions, which are mutually exclusive and jointly exhaustive):
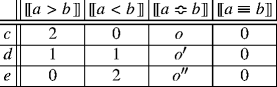
Then, by (Qualitative Simplification) and by the same argument as in case 1, we have: a ≽ b iff c ≽ d iff d ≽ e. Since a ≽ b (by hypothesis), we have that c ≽ d and d ≽ e. Then, by (Transitivity), c ≽ e. Recall that N = a ≢ b and B = a > b. So f N ∩ B and \(f_{N \cap \overline B}\) can be expressed by:
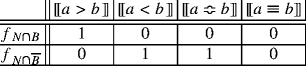
Then, since o′ ≻ o, it follows from (Qualitative Simplification) that c ≽ e iff \(f_{N \cap B} \succeq f_{N \cap \overline B}\). Since c ≽ e, we conclude that \(f_{N \cap B} \succeq f_{N \cap \overline B}\), as required. Argue as follows that:
$$\begin{array}{@{}rcl@{}} f_{N \cap B} \;\succeq\; f_{N \cap \overline B} &\implies& a \succeq b. \end{array}$$Suppose that \(f_{N \cap B} \succeq f_{N \cap \overline B}\). By (Regularity), there are non-comparable outcomes o, o′ that have a common upper or lower bound. Case 2.1: o and o′ have a common upper bound o ∗; namely: \(o^{*} \succ o \Bumpeq o' \prec o^{*}\). Define acts g, h ∗, i as follows:
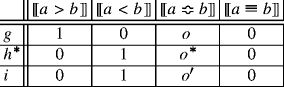
Then, by (Qualitative Simplification), \(f_{N \cap B} \succeq f_{N \cap \overline B}\) iff g ≽ h ∗. So, since \(f_{A \cap B} \succeq f_{\overline {A} \cap B}\) (by hypothesis), we have that g ≽ h ∗. But h ∗ ≽ i, by (Dominance). So, by (Transitivity), we have that g ≽ i. Then, by (Qualitative Simplification), g ≽ i iff a ≽ b. Hence, a ≽ b. Case 2.2: o and o′ have a common lower bound o ∗. So we have that \(o_{*} \prec o \Bumpeq o' \succ o_{*}\). Define act h ∗, to be compared to the acts g, i that we have defined:
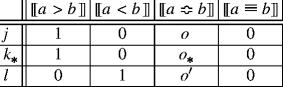
By the same argument, we have: j ≽ k ∗, by (Dominance); \(f_{N \cap B} \succeq f_{N \cap \overline B}\) iff k ∗ ≽ l, by (Qualitative Simplification); k ∗ ≽ l (since \(f_{N \cap B} \succeq f_{N \cap \overline B}\) by hypothesis); hence, j ≽ l, by (Transitivity). But j ≽ l iff a ≽ , by (Qualitative Simplification). So a ≽ b, as required.
By Case 1 and 2, we have established that a ≽ b iff \(f_{N \cap B} \succeq f_{N \cap \overline B}\), as required. □
Lemma 6
For all propositions A, B:
Proof
Bel(A ⇒ B) is equivalent to \(f_{A \cap B} \;\succeq \; f_{A \cap \overline B}\) (by definition), which is equivalent to \(f_{A \cap (A \cap B)} \;\succeq \; f_{A \cap \overline {(A \cap B)}}\) (by the Boolean algebra of sets), which is equivalent to Bel(A ⇒ A ∩ B) (by definition). □
Lemma 7
Bel satisfies (And).
Proof
Let A, B, X be arbitrary propositions. Suppose that Bel(X ⇒ A) and Bel(X ⇒ B). Define acts i, j, k as follows (note that the five propositions in the first row are mutually exclusive and jointly exhaustive, where concatenation means conjunction):Footnote 21

Since Bel(X ⇒ A), we have that Bel(X ⇒ A ∩ X) (by Lemma 6). According to the table, X = [[i ≢ j]] and A ∩ X = [[i > j]]. So Bel([[i ≢ j]] ⇒ [[i > j]]). Then, by Lemma 5, i ≽ j. By the same argument (with A replaced by B and ij replaced by jk), we have that j ≽ k. Then, by (Transitivity), we have that i ≽ k. So, by Lemma 5, Bel([[i ≢ k]] ⇒ [[i > k]]). But [[i ≢ k]] = X and [[i > k]] = A B X (by the table). So substitution yields that Bel(X ⇒ A B X). Hence, by Lemma 6, Bel(X ⇒ A ∩ B). □
To prove that Bel satisfies (Cautious Monotonicity), we will employ some earlier results plus:
Lemma 8
Bel satisfies:
Proof
Suppose that Bel(A ⇒ B) and B ⊆ X. Then, since Bel(A ⇒ B), \(f_{A \cap B} \succeq f_{A \cap \overline B}\). Also, by (Dominance), \(f_{A \cap \overline B} \succeq f_{A \cap X \cap \overline B}\). So, to recap, we have: \(f_{A \cap X \cap B} = f_{A \cap B} \succeq f_{A \cap \overline B} \succeq f_{A \cap X \cap \overline B}\). Then, by (Transitivity), \(f_{A \cap X \cap B} \succeq f_{A \cap X \cap \overline B}\). So, by definition, Bel(A ∩ X ⇒ B). □
Lemma 9
Bel satisfies (Cautious Monotonicity).
Proof
It is routine to prove that (Cautious Monotonicity) follows from (Right Weakening), (And), and (Hypothetico-Deductive Monotonicity). So the present lemma is an immediate consequence of Lemmas 4, 7, and 8. □
To prove that Bel satisfies (Or), we will employ some earlier results plus:
Lemma 10
Bel satisfies:
Proof
Suppose that Bel(A ⇒ B) and \(A \cap X = \varnothing \). So, by definition, \(f_{A \cap B} \succeq f_{A \cap \overline B}\). By Boolean algebra, A ∩ B ⊆ (A ∪ X) ∩ (B ∪ X). Then, by (Dominance), f (A ∪ X) ∩ (B ∪ X) ≽ f A ∩ B . By \(A \cap X = \varnothing \) and Boolean algebra, \(A \cap \overline B = (A \cup X) \cap \overline {(B \cup X)}\). So, to recap, \(f_{(A \cup X) \cap (B \cup X)} \succeq f_{A \cap B} \succeq f_{A \cap \overline B} = f_{(A \cup X) \cap \overline {(B \cup X)}}\). Hence, by (Transitivity), we have that \(f_{(A \cup X) \cap (B \cup X)} \succeq f_{(A \cup X) \cap \overline {(B \cup X)}}\). Then, by definition, we have that Bel(A ∪ X ⇒ B ∪ X), as required. □
Lemma 11
Bel satisfies (Or).
Proof
It is routine to prove that (Or) follows from (And) plus (Weak Or). So the present lemma is an immediate consequence of Lemmas 7 and 10. □
Lemma 12
Bel is consistent and closed under system ℙ.
Proof
Immediate from Lemmas 2, 3, 4, 7, 9, and 11. □
Lemma 13
(Existence) Preference relation ≽ is represented by the basic rules for everyday decision with respect to 〈≥, Bel〉, where Bel is consistent and closed under system ℙ and ≥ is reflexive and transitive.
Proof
Immediate from Proposition 2 and Lemmas 1, 5, and 12. □
Lemma 14
(Uniqueness) Suppose that ≽ is represented by the basic rules with respect to 〈≥′ , Bel′ 〉, where ≥′ is a desirability oder over outcomes and Bel′ is a conditional belief set closed under the minimal system: (Reflexivity ), (Weak And ), (Right Weakening ), and (Hypothetico-Deductive Monotonicity ). Then: ≥′ = ≥ and Bel′ = Bel. And hence: ≥′ is reflexive and transitive, and Bel′ is consistent and closed under system ℙ.
Proof
First, argue as follows that Bel′ is consistent. Suppose for reductio that it is not consistent. Then, Bel′ (S ⇒ ∅). Let ¬ A be the negation of an arbitrary proposition. Since ∅ ⊆ ¬ A, it follows from (Hypothetico-Deductive Monotonicity) that Bel′ (¬A ∩ S ⇒ ∅), namely Bel′ (¬A ⇒ ∅), namely Sure′ (A). So Sure′ (A), for each proposition A ⊆ S. Then, by representability with respect to ≥ ′ , Bel′ , we have that o 1 ∼ o 2for all outcomes o 1, o 2 ∈ O. But that contradicts the (Regularity) condition.
Argue as follows that ≥ ′ = ≥ . Let o 1, o 2be arbitrary outcomes in O. Then it suffices to show that o 1 ≥ ′ o 2iff o 1 ≥ o 2. Suppose that o 1 ≥ ′ o 2(and we want to show that o 1 ≥ o 2). Case 1: o 1 ≡ ′ o 2. Then Bel′ ([[o 1 ≢′ o 2 ]] = ∅, and, hence, Bel′ ([[o 1 ≢′ o 2]] ⇒ ∅) by (Reflexivity). Then, by representability with respect to 〈≥ ′ , Bel′ 〉, we have that o 1 ∼ o 2. Then, by Lemma 13 and the basic rules with respect to ≥ , Bel, we have that Bel′ ([[o 1 ≢′ o 2]] ⇒ ∅). Note that [[o 1 ≢ o 2]] = S or ∅, because o 1 and o 2are constant acts. Since Bel is consistent, [[o 1 ≢ o 2]] cannot be S and, hence, has to be ∅. So o 1 ≡ o 2. Hence, o 1 ≥ o 2. Case 2: o 1 >′ o 2. Then [[o 1 >′ o 2]] = S. So, by (Reflexivity), we have that Bel′ (S ⇒ [[o 1 >′ o 2]]). Then, by representability with respect to 〈≥ ′ , Bel′ 〉, we have that o 1 ≻ o 2. Then, by Lemma 13 and the basic rules with respect to 〈≥ , Bel〉, we have that: ether Bel(S ⇒ [[o 1 > o 2]]), or Bel([[o 1 ≢ o 2]] ⇒ [[o 1 > o 2]]). Then, by the consistency of Bel and by the same argument as the preceding case, we have that [[o 1 > o 2]] = S. Namely, o 1 > o 2. So o 1 ≥ o 2. We have established that o 1 ≥ ′ o 2implies o 1 ≥ o 2, and the converse can be derived by the same argument with Bel and Bel′ exchanged, and with ≥ and ≥′ . (Note that we earlier employed the reflexivity and consistent of Bel; for Bel′ , reflexivity is a premise and consistency has been established).
Argue as follows that Bel′ = Bel. Let A, B be arbitrary propositions. It suffices to show that Bel′ (A ⇒ B) iff Bel(A ⇒ B). Suppose that Bel′ (A ⇒ B) (and we want to show that Bel(A ⇒ B)). Consider acts f A ∩ B and \(f_{A \cap \overline B}\). Also note that, since ≥ ′ = ≥ , we have that 1 > ′ 0. Case I: Bel′(¬A ⇒ ∅). Then, by representability with respect to 〈≥ ′, Bel′〉 , \(f_{A \cap B} \sim f_{A \cap \overline B}\). So \(f_{A \cap B} \succeq f_{A \cap \overline B}\). Then, by the definition of Bel, we have that Bel(A ⇒ B), as required. Case II: ¬Bel′(¬A ⇒ ∅). Also, since Bel′ (A ⇒ B), we have that Bel′ (A ⇒ A ∩ B) by (Weak And). Then, by representability with respect to 〈 ≥ ′ , Bel′〉, \(f_{A \cap B} \succ f_{A \cap \overline B}\). So \(f_{A \cap B} \succeq f_{A \cap \overline B}\). Then, by the definition of Bel, we have that Bel(A ⇒ B), as required. For the converse, suppose that Bel(A ⇒ B) (and we want to show that Bel′ (A ⇒ B)). Then, by the definition of Bel, we have that \(f_{A \cap B} \succeq f_{A \cap \overline B}\). Case α: \(f_{A \cap B} \sim f_{A \cap \overline B}\). Note that \(f_{A \cap B}(s) \not \equiv ' f_{A \cap \overline B}(s)\) iff s ∈ A. Then, by representability with respect to 〈≥ ′ , Bel′〉, we have that \({\sf Bel}'(A\Rightarrow \varnothing )\). So, by (Right Weakening), Bel′ (A ⇒ B). Case β: \(f_{A \cap B} \succ f_{A \cap \overline B}\). Then, by representability with respect to 〈≥ ′, Bel′〉 , either Bel′ (S ⇒ A ∩ B), or Bel′ (A ⇒ A ∩ B). The first disjunct implies the second disjunct. For, if Bel′ (S ⇒ A ∩ B), then, since A ∩ B ⊆ A, we have, by (Hypothetico-Deductive Monotonicity), that Bel′ (A ⇒ A ∩ B). It follows that Bel′ (A ⇒ A ∩ B). Then, by (Right Weakening), Bel′ (A ⇒ B). □
Theorem 3 follows immediately from the existence Lemma 13 and the uniqueness Lemma 14.
Appendix E: Freedom from Constant Acts
Constant acts are not essential to the representation Theorem 2 plus 3. Whenever we make use of o ≻ o′ , the only property we need for the proof is that, for each state s, the outcome of act o in s is preferred to the outcome of act o′ in s—namely, act o is preferred to act o′ given each state s ∈ S. In the present paper, we never need to compare an outcome at a state with another outcome at a distinct state. That is required by the basic rules for everyday decision, and also required by the (Qualitative Simplification) axiom. The same holds not only for ‘ ≻ ’ but also for ‘ ∼ ’ and ‘≎’. Accordingly, modify the definitions in the paper as follows. A decision problem is specified by a set S of states such that the states s in S are associated with disjoint sets O s of outcomes, where o ∈ O s means that outcome o is possible in state s.Footnote 22 An act is a function a that maps each s ∈ S to an outcome a(s) ∈ O s (i.e., a is a choice function over the product space \(\prod _{s \in S} O_{s}\)). Desirability orders ≥ are binary relations over the set of all outcomes, \(\bigcup _{s \in S} O_{s}\). Preference relations ≽ are understood as containing two kinds of data: for acts a and b, a ≽ b means that a is at least as preferable as b; for outcomes o and o′ that are possible in the same state s, o ≽ o′ means that o is at least preferable as o′ given that s is the actual state. So a(s) ≽ b(s) is to be understood as conditional preference given s in axioms (Dominance) and (Qualitative Simplification). The (Regularity) condition in its original form is about the outcome set O; now replace it by the requirement that, for each s ∈ S, (Regularity) holds for O s . Then the representation Theorem 2 and 3 are still true—except that, in the theorem for complete representation, the existence of the required desirability order ≥ is unique only up to restriction to O s for each state s ∈ S (that is, the relative desirability between two outcomes that are possible in different states may not be unique).
Constant acts are essential only to the “only if” side of Theorem 1. When each state s is associated with its own set O s of possible outcomes, the “if” side of Theorem 1 is still true; namely, we still have the same sufficiency condition for (Consistency with Bayesian Preference).
Appendix F: Comparison with the Pioneering Work of Dubois et al. [7]
Dubois et al. [7] does not intend their pioneer work to be about everyday practical reasoning, but it is their work that makes me realize that it is possible to provide a Savage-like foundation for everyday practical reasoning. But, in order to capture important features of everyday practical reasoning, I have to weaken their axiomatization and modify their modeling assumptions in a number of ways, as explained the following.
-
1.
Axiomatization. First, the set of my axioms for preference is strictly weaker than theirs (what they call: WS1, WSTP, S3, S5, and OI). I have four axioms. The first three axioms (Reflexivity), (Transitivity), and (Dominance) are so basic that they are entailed by Dubois et al.’s axiomatization (and probably entailed by almost all axiomatizations in the literature). My last axiom is (Qualitative Simplification), which is an immediate consequence of Dubois et al.’s Ordinal Invariance (OI) axiom. So my axiomatization is at least as weak as Dubois. In fact, mine is strictly weaker, because their axiomatization has a consequence that mine does not have, namely that the strict desirability order > is rankable, or equivalently, that the non-strict desirability order ≥ is a weak order (i.e., reflexive, transitive, and complete). That is stated in their proposition 8, whose proof makes essential use of their Ordinal Invariance (OI) axiom.
-
2.
Desirability. There is a subtle difference in the ways we model desirability over outcomes. Dubois et al. take the concept of “being more desirable than” ( > ) as primitive, which is unable to distinguish “equally desirable” from “non-comparable”. Instead, I take the concept of “being at least as desirable as” ( ≥ ) as primitive in order to distinguish “equally desirable” from “non-comparable”, which is crucial for the project I pursue. In qualitative decision-making, one may have to treat two outcomes as non-comparable (at least for the time being) because, for example, the time available may be too short for the agent to think it through. And that is very different from the judgment that two outcomes are equally desirable. As mentioned in the preceding paragraph, Dubois et al. require that a strict desirability order > over outcomes be rankable, in the sense that the relation R defined below is transitive: o 1 R o 2iff o 1 ≯ o 2and o 2 ≯ o 1. In their formal framework, the statement “ o 1 R o 2” does not say whether the two outcomes are equally desirable or non-comparable, and each of the two interpretations would make the rankability requirement too strong. Case 1: if R is understood to express equal desirability for all instances, then the requirement is equivalent to saying that we take ≥ as primitive and require it to be reflexive, transitive, and complete and, hence, there are no non-comparable outcomes. Case 2: if R is understood to express non-comparable desirability for all instances, then the requirement is equivalent to saying that we take ≥ as primitive, that no two distinct outcomes are equally desirable, and that the non-comparability relation of desirability is transitive.Footnote 23
-
3.
Preference. There is a corresponding difference in the ways we model preference over acts. Dubois et al. employ the concept of “being strictly more preferable than” as primitive. But I employ the concept of “being at least as preferable as” as primitive. I do so because I need to distinguish equal preference from non-comparable preference, which is crucial for explaining how everyday practical reasoning may work with Bayesian decision-making. Suppose that an agent is choosing between two acts. If those two acts are judged to be equally preferable by a kind of qualitative decision-making, the agent is advised to choose either. But things are very different if the two acts are left non-comparable because, say, everyday practical reasoning is too coarse to make the two acts comparable. In that case, the agent is provided with no advice at all from everyday practical reasoning, and she may wish to consider resorting to a more refined style of decision-making (such as maximization of expected utility), or just choosing one arbitrarily (in order to save some deliberation cost).
-
4.
Belief. The kind of belief representation that Dubois et al. adopt is based on the idea that one proposition is “more likely than” another proposition, which they call a subjective likelihood relation > L .Footnote 24 They also explain how each subjective likelihood relation can be used to define a nonmonotonic consequence relation, or what I call a conditional belief set:
$${\sf Bel}(A \Rightarrow B) \mbox{iff} A \cap B >_{L} A \cap \overline{B}.$$(23)So there is no essential difference in belief representations. But the non-monotonic logics derived are slightly different. The present work derives system ℙ, while Dubois and his colleagues derive system ℙ minus (Reflexivity). The difference comes down to the following: Let A be a decision- theoretically null proposition (i.e., the preference relation is independent of what outcomes are produced at the states in A). I still have Bel(A ⇒ A)in conformity to (Reflexivity) and, furthermore, I have Bel(A ⇒ X) for each proposition X ⊆ S. But Dubois et al. have ¬ Bel(A ⇒ A), which violates (Reflexivity) and the reason is rooted in their decision rule (see their discussion in Section 5.3).
-
5.
Decision Rule. The difference in decision rules is the following. For Dubois et al., each strict desirability order > and each subjective likelihood relation > L jointly determine a strict preference relation ≻ as follows:
$$\begin{array}{@{}rcl@{}} a \succ b &\mbox{iff}& [[ a > b ]] \;>_{L}\; [[ a < b ]], \end{array}$$(24)which implies, by definition (23), that:
$$ \mathrm{(Dubois et al.)} \quad\quad a \succ b \mathrm{iff} {\sf Bel}([[ a > b]] \cup [[ a < b]] \Rightarrow [[ a > b]]).$$(25)That is a restatement of Dubois et al.’s decision rule in my terminology. Now we can compare it to my decision rules. An elegant form for strict preference in my theory is formula (5), which is reproduced in the following for ease of comparison:
$$ \mathrm{(My \,\,Proposal)} {\kern7pt} a \succ b \text{iff} \neg {\sf Bel}([[ a \not\equiv b ]] \Rightarrow \bot) \,\,\text{and}\, {\sf Bel}([[ a \not\equiv b ]] \Rightarrow [[ a > b]]).\\ $$(26)Assuming that Bel satisfies (Left Weakening) and (Cautious Monotonicity) and that ≥ is reflexive and transitive, the left-hand side of (25) is is implied by the second conjunct in the left-hand side of (26).Footnote 25 So Dubois et al’s criterion for strict preference is weaker than my criterion, which is ultimately motivated from examples of everyday practical reasoning. Furthermore, I have a decision rule for equal preference (which is distinguished from non-comparability), but Dubois et al. do not.
Rights and permissions
About this article
Cite this article
Lin, H. Foundations of Everyday Practical Reasoning. J Philos Logic 42, 831–862 (2013). https://doi.org/10.1007/s10992-013-9296-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-013-9296-0