Randomness of the square root of 2 and the giant leap, part 2

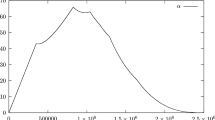
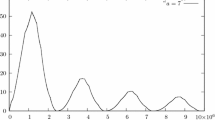
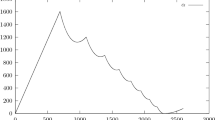
Abstract

We prove that the “quadratic irrational rotation” exhibits a central limit theorem. More precisely, let α be an arbitrary real root of a quadratic equation with integer coefficients; say, $\alpha = \sqrt 2$ . Given any rational number 0 < x < 1 (say, x = 1/2) and any positive integer n, we count the number of elements of the sequence α, 2α, 3α, ..., nα modulo 1 that fall into the subinterval [0, x]. We prove that this counting number satisfies a central limit theorem in the following sense. First, we subtract the “expected number” nx from the counting number, and study the typical fluctuation of this difference as n runs in a long interval 1 ≤ n ≤ N. Depending on α and x, we may need an extra additive correction of constant times logarithm of N; furthermore, what we always need is a multiplicative correction: division by (another) constant times square root of logarithm of N. If N is large, the distribution of this renormalized counting number, as n runs in 1 ≤ n ≤ N, is very close to the standard normal distribution (bell shaped curve), and the corresponding error term tends to zero as N tends to infinity. This is the main result of the paper (see Theorem 1.1).