Opportunistic Fair Scheduling in Wireless Networks: An Approximate Dynamic Programming Approach

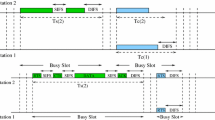
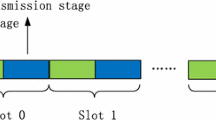
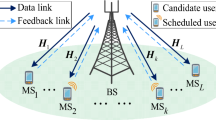
Abstract

We consider the problem of temporal fair scheduling of queued data transmissions in wireless heterogeneous networks. We deal with both the throughput maximization problem and the delay minimization problem. Taking fairness constraints and the data arrival queues into consideration, we formulate the transmission scheduling problem as a Markov decision process (MDP) with fairness constraints. We study two categories of fairness constraints, namely temporal fairness and utilitarian fairness. We consider two criteria: infinite horizon expected total discounted reward and expected average reward. Applying the dynamic programming approach, we derive and prove explicit optimality equations for the above constrained MDPs, and give corresponding optimal fair scheduling policies based on those equations. A practical stochastic-approximation-type algorithm is applied to calculate the control parameters online in the policies. Furthermore, we develop a novel approximation method—temporal fair rollout—to achieve a tractable computation. Numerical results show that the proposed scheme achieves significant performance improvement for both throughput maximization and delay minimization problems compared with other existing schemes.

Appendix

1.1 A Proof of Lemma 1

Proof

Let π be an arbitrary policy, and suppose that π chooses action a at time slot 0 with probability P _a , a ∈ A. Then,

$$ V_{\pi}(s)=\sum_{a\in A}P_{a}\left[r(s,a)+ u(a) +\sum_{s'\in S}P(s'|s,a)W_{\pi}(s')\right], $$

where W _π (s′) represents the expected discounted weighted reward with the weight u(π _t ) incurred from time slot 1 onwards, given that π is employed and the state a time 1 is s′. However, it follows that

$$ W_{\pi}(s')\leq \alpha V_{\alpha}(s') $$

and hence that

$$\begin{array}{rl} V_{\pi}(s)&\leq \sum\limits_{a\in A}P_{a}\left\{r(s,a)+ u(a) +\alpha\sum\limits_{s'\in S}P(s'|s,a)V_{\alpha}(s')\right\} \\ &\!\leq\! \sum\limits_{a\in A}P_{a}\max\limits_{a\in A}\!\left\{r(s,a)\!+\! u(a) \!+\!\alpha\!\sum\limits_{s'\in S}P(s'|s,a)V_{\alpha}(s')\right\} \\ &=\max\limits_{a\in A}\left\{r(s,a)+ u(a) +\alpha\sum\limits_{s'\in S}P(s'|s,a)V_{\alpha}(s')\right\}.\label{Lemma1.2} \end{array} $$

(23)

Since π is arbitrary, Eq. 23 implies that

$$ \label{Lemma1.3} V_{\alpha}(s)\leq\max_{a\in A}\left\{r(s,a)+u(a)+\alpha\sum_{s'\in S}P(s'|s,a)V_{\alpha}(s')\right\}. $$

(24)

To go the other way, let a ₀ be such that

$$ \begin{array}{rcl} \label{Lemma1.4} &&{\kern-6pt} r(s,a_0)+u(a_0)+\alpha\sum\limits_{s'\in S}P(s'|s,a_0)V_{\alpha}(s') \\ &&=\max\limits_{a\in A}\left\{r(s,a)+u(a)+\alpha\sum\limits_{s'\in S}P(s'|s,a)V_{\alpha}(s')\right\} \end{array} $$

(25)

and let π be the policy that chooses a ₀ at time 0; and, if the next state is s′, views the process as originating in state s′; and follows a policy π _s′, which is such that $V_{\pi_{s'}}(s')\geq V_{\alpha}(s')-\varepsilon$, s′ ∈ S. Hence,

$$ \begin{array}{rl} V_{\pi}(s)&=r(s,a_0)+u(a_0)+\alpha\sum\limits_{s'\in S}P(s'|s,a_0)V_{\pi_{s'}}(s') \\ &\geq r(s,a_0)+u(a_0)+\alpha\sum\limits_{s'\in S}P(s'|s,a_0)V_{\alpha}(s')-\alpha \varepsilon \end{array} $$

which, since V _α (s) ≥ V _π (s), implies that

$$ V_{\alpha}(s)\geq r(s,a_0)+u(a_0)+\alpha\sum_{s'\in S}P(s'|s,a_0)V_{\alpha}(s')-\alpha \varepsilon. $$

Hence, from Eq. 25, we have

$$ \label{Lemma1.5} V_{\alpha}(s)\!\geq\! \max_{a\in A}\left\{r(s,a)\!+\!u(a)\!+\!\alpha\sum_{s'\in S}P(s'|s,a)V_{\alpha}(s')\right\}\!-\!\alpha \varepsilon. $$

(26)

Since π _s′ could be arbitrary, then ε is arbitrary, from Eqs. 24 and 26, we have

$$ \begin{array}{rcl} V_{\alpha}(s)&=&\max\limits_{a\in A}\left\{r(s,a)+u(a). +\alpha\sum\limits_{s'\in S}P(s'|s,a)V_{\alpha}(s')\right\},\\ s &\in& S. \end{array} $$

□

1.2 B Proof of Lemma 2

Proof

By applying the mapping $T_{\pi^*}$ to V _α , we obtain

$$ \begin{array}{rcl} &&{\kern-30pt}(T_{\pi^*}V_\alpha)(s) \\ \quad{\kern6pt}&=&r(s,\pi^*(s))+u(\pi^*(s)) +\alpha\sum\limits_{s'\in S}P(s'|s,\pi^*(s))V_\alpha(s')\\ \quad&=&\!\max\limits_{a\in A}\!\left\{r(s,a)\!+\!u(a)\!+\!\!\alpha\!\sum\limits_{s'\in S}\!P(s'|s,\pi^*(s))\!V_\alpha(s')\!\right\}\!\!=\!\!V_\alpha\!(s), \end{array} $$

where the last equation follows from Lemma 1. Hence, by induction we have,

$$ T_{\pi^*}^nV_\alpha=V_\alpha , \quad \forall n. $$

Letting n→ ∞ and using Banach fixed-point theorem yields the result,

$$ V_{\pi^*}(s)=V_\alpha(s), \quad \forall s \in S. $$

□

1.3 C Proof of Theorem 1

Proof

Let π be a policy satisfying the expected discounted temporal fairness constraint. And suppose there exists u:A→ℝ satisfying conditions 1–3. Then,

$$ \begin{array}{rcl} &&{\kern-30pt}J_{\pi}(s)\\ {\kern6pt} \;\;&=&\lim\limits_{T\to\infty}E_{\pi}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}r(X_t,\pi_t)\right|X_0=s\right]\\ \;\;&\leq& \lim\limits_{T\to\infty}E_{\pi}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}r(X_t,\pi_t)\right|X_0=s\right]\\ &&+\!\sum\limits_{a\in A}u(a)\!\left(\lim\limits_{T\to\infty}E_{\pi}\left[\left.\sum\limits^{T-1}_{t=0}\alpha^t\mathbf{1}_{\{\pi_t=a\}}\right|X_0=s\right]\!-\!C(a)\right)\\ \;\;&=&\lim\limits_{T\to\infty}E_{\pi}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}r(X_t,\pi_t)\right|X_0=s\right]\\ &&+\lim\limits_{T\to\infty}E_{\pi}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^tu(\pi_t)\right|X_0=s\right]-\sum\limits_{a \in A}u(a)C(a)\\ \;\;&=& \lim\limits_{T\to\infty}E_{\pi}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}[r(X_t,\pi_t)+u(\pi_t)]\right|X_0=s\right]\\ &&-\sum\limits_{a\in A}u(a)C(a)\\ \;\;&=&V_{\pi}(s)-\sum\limits_{a\in A}u(a)C(a). \end{array} $$

Since $V_{\pi}(s)\leq V_{\alpha}(s)=V_{\pi^*}(s)$ from Lemma 2, we have

$$ J_{\pi}(s)\leq V_{\pi^*}(s)-\sum_{a\in A}u(a)C(a)\label{Theorem1.1} $$

(27)

$$ \begin{array}{rcl} \quad&&=\lim\limits_{T\to\infty}E_{\pi^*}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}[r(X_t,\pi^*_t)+u(\pi^*_t)]\right|X_0=s\right] \\[5pt] &&{\kern6pt}-\sum\limits_{a\in A}u(a)C(a) \\[5pt] &&=\lim\limits_{T\to\infty}E_{\pi^*}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}r(X_t,\pi^*_t)\right|X_0=s\right] \\[5pt] &&{\kern6pt}+\,\sum\limits_{a\in A}u(a)\left(\lim\limits_{T\to\infty}E_{\pi^*}\!\left[\left.\sum\limits^{T-1}_{t=0}\alpha^t\mathbf{1}_{\{\pi^*_t=a\}}\right|X_0\!=\!s\right]\!-\!C(a)\!\right) \\[5pt] &&=\lim\limits_{T\to\infty}E_{\pi^*}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}r(X_t,\pi^*_t)\right|X_0=s\right] \\[5pt] &&=J_{\pi^*}(s),\label{Theorem1.2} \end{array} $$

(28)

where the second part of Eq. 28 equals zero because of condition 3 on u. From Eq. 27, we get the corresponding optimal discounted reward as

$$ J_{\pi^*}(s)=V_{\pi^*}(s)-\sum_{a \in A}u(a)C(a) , \; \forall s \in S. $$

□

1.4 D Proof of Theorem 2

Proof

Let π be a policy satisfying the expected average temporal fairness constraint; and let H _t  = (X ₀,π ₀,..., X _t − 1,π _t − 1,X _t ,π _t ) denote the history of the process up to time t. First, we have

$$E_{\pi}\left\{\sum_{t=1}^T[h(X_t)-E_{\pi}(h(X_t)|H_{t-1})]\right\}=0,$$

since

$$ \begin{array}{rcl} &&{\kern-21pt}E_{\pi}\left\{\sum\limits_{t=1}^T[h(X_t)-E_{\pi}(h(X_t)|H_{t-1})]\right\} \\ {\kern6pt}\;\;&=&\sum\limits_{t=1}^T E_{\pi}[h(X_t)-E_{\pi}(h(X_t)|H_{t-1})] \\ \;\;&=&\sum\limits_{t=1}^T \{E_{\pi}[h(X_t)]-E_{\pi}[E_{\pi}(h(X_t)|H_{t-1})]\} \\ \;\;&=&\sum\limits_{t=1}^T \{E_{\pi}[h(X_t)]-E_{\pi}[h(X_t)]\}=0. \end{array} $$

Also,

$$ \begin{array}{rcl} E_{\pi}[h(X_t)|H_{t-1}]&=&\sum\limits_{s'\in S}h(s')P(s'|X_{t-1},\pi_{t-1})\\ &=&\; r(X_{t-1},\pi_{t-1})+u(\pi_{t-1})\\ &&+\sum\limits_{s'\in S}h(s')P(s'|X_{t-1},\pi_{t-1})\\ &&-r(X_{t-1},\pi_{t-1})-u(\pi_{t-1})\\ &\leq &\max\limits_{a\in A}\bigg\{r(X_{t-1},a)+u(a)\\ &&\phantom{\max\limits_{a\in A}\,\,}+\sum_{s'\in S}P(s'|X_{t-1},a)h(s')\bigg\}\\ &&-r(X_{t-1},\pi_{t-1})-u(\pi_{t-1})\\ &=& g\!+\!h(X_{t-1})\!-\!r(X_{t-1},\pi_{t-1})\!-\!u(\pi_{t-1}) \end{array} $$

with equality for π ^*, since π ^* is defined to take the maximizing action. Hence,

$$ \begin{array}{rcl} 0&\geq& E_{\pi}\Bigg\{\sum\limits_{t=1}^T\big[h(X_t)-g-h(X_{t-1})+r(X_{t-1},\pi_{t-1})\Bigg.\\ &&\phantom{E_{\pi}\,\,}\Bigg.+u(\pi_{t-1})\big]\Bigg\}\\ \Leftrightarrow g&\geq& E_{\pi}\frac{h(X_T)}{T}-E_{\pi}\frac{h(X_0)}{T}+E_{\pi}\frac{1}{T}\sum\limits_{t=1}^Tr(X_{t-1},\pi_{t-1})\\ &&+E_{\pi}\frac{1}{T}\sum\limits_{t=1}^Tu(\pi_{t-1}). \end{array} $$

Letting T → ∞ and using the fact that h is bounded, we have that

$$ \begin{array}{rl} g&\geq J_{\pi}(X_0)+\lim\limits_{T\to \infty}E_{\pi}\frac{1}{T}\sum\limits_{t=0}^{T-1}u(\pi_t) \Leftrightarrow g-\sum\limits_{a\in A}u(a)C(a) \\&\geq J_{\pi}(X_0)+\lim\limits_{T\to \infty}E_{\pi}\frac{1}{T}\sum\limits_{t=0}^{T-1}u(\pi_t)-\sum\limits_{a\in A}u(a)C(a) \\ &= J_{\pi}(s)+\lim\limits_{T\to \infty}E_{\pi}\bigg[\left.\frac{1}{T}\sum\limits_{t=0}^{T-1}\sum\limits_{a\in A}u(a)\mathbf{1}_{\{\pi_t=a\}}\right|\, X_0=s\bigg] \\ &{\kern6pt}-\sum\limits_{a\in A}u(a)C(a) \\ &= J_{\pi}(s)+\sum\limits_{a\in A}u(a)\bigg(\lim\limits_{T\to \infty}E_{\pi}\bigg[\left.\frac{1}{T}\sum\limits_{t=0}^{T-1}\mathbf{1}_{\{\pi_t=a\}}\right|\, X_0=s\bigg] \\ &{\kern6pt}-C(a)\bigg).\label{Theorem2.1} \end{array}$$

(29)

Since we know that u ≥ 0, and that the policy π satisfies the temporal fairness constraints, the second part of Eq. 29 is greater than or equal to zero. We get

$$ g-\sum_{a\in A}u(a)C(a)\geq J_{\pi}(s). $$

With policy π ^*, we have

$$ \begin{array}{l} g\!-\!\sum\limits_{a\in A}u(a)C(a)= J_{\pi^*}(s)\\ \qquad \qquad \quad\!+\!\sum\limits_{a\in A}u(a) \times \bigg(\!\lim\limits_{T\to\infty}\!E_{\pi^*}\left[\!\frac{1}{T}\sum\limits_{t=0}^{T-1}\mathbf{1}_{\{\pi_t^*=a\}}\!\right]\!-\!C(a)\!\bigg) \\ \qquad \qquad \qquad = J_{\pi^*}(s), \end{array} $$

(30)

where the second part of Eq. 30 equals to zero because of condition 3 on u(a). Hence, the desired result is proven. □

1.5 E Proof of Theorem 3

Proof

Let π be a policy satisfying the expected discounted utilitarian fairness constraint. And suppose there exists ω:A→ℝ satisfying conditions 1–3. Then,

$$ \begin{array}{rl} J_{\pi}(s) &\!\leq\! J_{\pi}(s)\!+\!\sum\limits_{a\in A}\omega(a)\Bigg(\!\lim\limits_{T\to\infty}E_{\pi}\Bigg[\left.\sum\limits^{T-1}_{t=0}\alpha^tr(X_t,\pi_t)\mathbf{1}_{\{\pi_t=a\}}\right| \\ &\qquad\qquad\qquad{\kern120pt} \times\! X_0 \!=\!s\!\Bigg]\!-\!D(a)J_{\pi}(s)\!\Bigg) \\ &=J_{\pi}(s)+\lim\limits_{T\to\infty}E_{\pi}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^t\omega(\pi_t)r(X_t,\pi_t)\right|X_0=s\right] \\ &{\kern12pt} -\sum\limits_{a \in A}\omega(a)D(a)J_{\pi}(s) \\ &=\lim\limits_{T\to\infty}E_{\pi}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}[(\kappa+\omega(\pi_t))r(X_t,\pi_t)]\right|X_0=s\right] \\ &=U_{\pi}(s), \end{array} $$

where $\kappa\!=\!1\!-\!\sum_{\pi_t\in A}D(\pi_t)\omega(\pi_t)$. Since U _π (s) ≤ U _α (s) = $U_{\pi^*}(s)$ from Lemma 4, we have

$$ J_{\pi}(s)\leq U_{\pi^*}(s)\label{Theorem3.1} $$

(31)

$$ \begin{array}{l} \qquad =\lim\limits_{T\to\infty}E_{\pi^*}\left[\left.\sum\limits_{t=0}^{T-1}\alpha^{t}r(X_t,\pi^*_t)\right|X_0=s\right] \\ + \sum\limits_{a\in A}\omega(a)\bigg(\!\lim\limits_{T\to\infty}E_{\pi^*}\bigg[\!\left.\sum\limits^{T-1}_{t=0}\alpha^tr(X_t,\pi^*_t)\mathbf{1}_{\{\pi^*_t\!=\!a\}}\right| X_0\!=\!s\!\bigg]\! \\ \qquad \qquad \qquad-\!D(a)J_{\pi^*}(s)\!\bigg) \\ \qquad =J_{\pi^*}(s), \end{array} $$

(32)

where the second part of Eq. 32 equals zero because of condition 3 on ω. From Eq. 31, we get the corresponding optimal discounted reward is

$$ J_{\pi^*}(s)=U_{\pi^*}(s) , \; \forall s \in S. $$

□

1.6 F Proof of Theorem 4

Proof

Let π be a policy satisfying the expected average utilitarian fairness constraint; and let H _t  = (X ₀,π ₀,..., X _t − 1,π _t − 1,X _t ,π _t ) denote the history of the process up to time t. First, we have

$$E_{\pi}\left\{\sum_{t=1}^T[h(X_t)-E_{\pi}(h(X_t)|H_{t-1})]\right\}=0.$$

Also,

$$ \begin{array}{rcl} E_{\pi}[h(X_t)|H_{t-1}]&=&\sum\limits_{s'\in S}h(s')P(s'|X_{t-1},\pi_{t-1})\\ &=& (\kappa+\omega(\pi_{t-1}))r(X_{t-1},\pi_{t-1})\\ &&+\,\sum\limits_{s'\in S}h(s')P(s'|X_{t-1},\pi_{t-1})\\ &&-\,(\kappa+\omega(\pi_{t-1}))r(X_{t-1},\pi_{t-1})\\ &\leq& \max\limits_{a\in A}\Bigg\{(\kappa+\omega(a))r(X_{t-1},a)\\ &&+\,\sum\limits_{s'\in S}P(s'|X_{t-1},a)h(s')\Bigg\}\\ &&-\,(\kappa+\omega(\pi_{t-1}))r(X_{t-1},\pi_{t-1})\\ &=&g+h(X_{t-1})-(\kappa+\omega(\pi_{t-1}))\\ &&\times\,r(X_{t-1},\pi_{t-1}) \end{array} $$

with equality for π ^*, since π ^* is defined to take the maximizing action. Hence,

$$ \begin{array}{rcl} 0&\geq& E_{\pi}\Bigg\{\sum\limits_{t=1}^T[h(X_t)-g-h(X_{t-1})\\ && +\,(\kappa+\omega(\pi_{t-1}))r(X_{t-1},\pi_{t-1})]\Bigg\}\\ \Leftrightarrow g&\geq&E_{\pi}\frac{h(X_T)}{T}-E_{\pi}\frac{h(X_0)}{T}\\ &&+\,E_{\pi}\frac{1}{T}\sum\limits_{t=1}^T(\kappa+\omega(\pi_{t-1}))r(X_{t-1},\pi_{t-1})\\ \Leftrightarrow g&\geq&E_{\pi}\frac{h(X_T)}{T}-E_{\pi}\frac{h(X_0)}{T}+E_{\pi}\frac{1}{T}\sum\limits_{t=1}^Tr(X_{t-1},\pi_{t-1})\\ &&+\,E_{\pi}\frac{1}{T}\!\sum\limits_{t=1}^T\left(\!\omega(\pi_{t-1}\!-\!\sum\limits_{a\in A}D(a) \omega(a)\right)\\ &&\times\,r(\!X_{t-1},\pi_{t-1}). \end{array} $$

Letting T → ∞ and using the fact that h is bounded, we have that

$$ \begin{array}{rll} g&\geq& J_{\pi}(X_0) \\ &+&\lim\limits_{T\to \infty}E_{\pi}\frac{1}{T}\sum\limits_{t=0}^{T-1}\left(\omega(\pi_{t-1}-\sum\limits_{a\in A}D(a)\omega(a)\right) r(X_{t-1},\pi_{t-1}) \\ \Leftrightarrow g &\geq& J_{\pi}(X_0) \\ &+& \sum\limits_{a\in A}\omega(a)\Bigg(\lim\limits_{T\to\infty}E_{\pi}\Bigg[\left.\frac{1}{T}\sum\limits^{T-1}_{t=0}r(X_t,\pi_t)\mathbf{1}_{\{\pi_t=a\}}\right| X_0=s\Bigg] \\ \qquad\qquad\qquad- D(a)J_{\pi}(s)\Bigg). \label{Theorem4.1} \end{array} $$

(33)

Since we know that ω ≥ 0, and that the policy π satisfies the utilitarian fairness constraints, the second part of Eq. 33 is greater than or equal to zero. We get

$$ g\geq J_{\pi}(s). $$

With policy π ^*, we have

$$ \begin{array}{lll} g&=& J_{\pi^*}(s) \\ \;\; +\sum\limits_{a\in A}u(a)\Bigg(\lim\limits_{T\to\infty}E_{\pi^*}\Bigg[\left.\frac{1}{T}\sum\limits^{T-1}_{t=0}r(X_t,\pi^*_t)\mathbf{1}_{\{\pi^*_t=a\}}\right| X_0\!=\!s\!\Bigg] \\ \qquad\qquad - D(a)J_{\pi^*}(s)\!\Bigg). \\ &=& J_{\pi^*}(s), \end{array} $$

(34)

where the second part of Eq. 34 equals to zero because of condition 3 on ω(a). Hence, the desired result is proven. □