Multi-channel energy detection under phase noise: analysis and mitigation

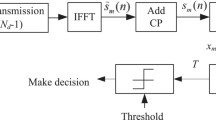
Abstract

For the development of highly integrated, flexible and low-cost cognitive radio (CR) devices, simple transceiver architectures, like direct-conversion receiver, are expected to be deployed and provide viable radio frequency (RF) spectrum sensing solutions for practical implementation. Yet, this can be very challenging task especially if spectrum sensing and down-conversion are conducted over multiple RF channels simultaneously for improved efficiency in channel scans. Then, the so-called dirty RF problem that degrades link performance of traditional transmission systems starts to be influential from spectrum sensing perspective as well. The unavoidable RF impairments, e.g., oscillator phase noise in direct-conversion receiver, could generate crosstalk between multiple channels that are down-converted simultaneously, and thus considerably limit the spectrum sensing capabilities. Most of the existing spectrum sensing studies in literature assume an ideal RF receiver and have not considered such practical RF hardware problem. In this article, we study the impact of oscillator phase noise on energy detection (ED) based spectrum sensing in multi-channel direct-conversion receiver scenario. With complex Gaussian primary user (PU) signal models, we first derive the detection and false alarm probabilities in closed-form expression. The analytical results, verified through extensive simulations, show that the wideband multi-channel sensing receiver is very sensitive to the neighboring channel crosstalk induced by oscillator phase noise. More specifically, it is shown that the false alarm probability of multi-channel energy detection increases significantly, compared to the ideal RF receiver case. The exact performance degradation depends on the power of neighboring channels as well as statistical characteristics of the phase noise in the deployed receiver. In order to prevent such performance degradation in spectrum identification, an enhanced energy detection technique is proposed. The proposed technique calculates the leakage power from neighboring channels for each channel and improves the sample energy statistics by subtracting this leakage power from the raw values. An analytical expression is derived for the leakage power which is shown to be a function of power spectral levels of neighboring channels and 3-dB bandwidth of phase noise process. Practical schemes for estimating these two quantities are discussed. Extensive computer simulations show that the proposed enhanced detection yields false alarm rates that are very close to those of an ideal RF receiver and hence clearly outperforms classical energy detection.

Appendix: Derivation of Variance of PU Signal and Interference Term

In this appendix, we will derive the expressions for variance of PU signal ($x_{k}^{\text {pn}}(n)$) and conditioned interference variance namely $\sigma _{x,\text {pn}}^{2}(k)$ and $\sigma _{z|\mathbf {\Theta }}^{2}(k)$.

For $R_{\tilde {x}}(k,m)=E[\tilde {x}_{k}(n)\tilde {x}_{k}^{*}(n-m)]$ and R _p (m) = E[p(n)p ^∗(n−m)] = a ^∣m∣ with a = e ^−2πβ/W, the auto-correlation $\tilde {x}_{k}^{\text {pn}}(n)=\big (\tilde {x}_{k}(n)p(n)\big )\otimes b(n)$ reads

$$\begin{array}{@{}rcl@{}} R_{\tilde{x},pn}(k,m)&=E[\tilde{x}_{k}^{\text{pn}}(n)(\tilde{x}_{k}^{\text{pn}}(n-m))^{*}] \\ &=\big(R_{\tilde{x}}(k,m)R_{p}(m)\big)\otimes b(m)\otimes b^{*}(-m) \\ &=\text{IDTFT}\{\big(S_{\tilde{x}}(k,f)\otimes S_{p}(k,f)\big) \mid B(f) \mid^{2} \} \\ &=\int_{-f_{\text{cut-off}}}^{f_{\text{cut-off}}} \big(S_{\tilde{x}}(k,f)\otimes S_{p}(k,f)\big)e^{j2\pi f m}df \end{array} $$

(29)

where the power spectral densities are given as

$$ S_{\tilde{x}}(k,f)=\text{DTFT}\{ R_{\tilde{x}}(k,m)\}=\begin{cases} &A_{k}, \hspace{0.1cm} \text{if} \mid f \mid \leq f_{\text{cut-off}}\\ &0, \hspace{0.3cm} \text{otherwise} \end{cases} $$

(30)

$$ S_{p}(f)=\text{DTFT}\{R_{p}(m)\}=\frac{1-a^{2}}{1-2acos(2\pi f)+a^{2}} $$

(31)

with $A_{k}={\sigma _{x}^{2}}(k)/(2f_{\text {cut-off}})$. Noting that the sampling rate does not alter the variance, the variance of the down-sampled term $x_{k}^{\text {pn}}(n):=\tilde {x}_{k}^{\text {pn}}(Ln)$ reads

$$\begin{array}{@{}rcl@{}} \sigma_{x,\text{pn}}^{2}(k)&=E[\mid x_{k}^{\text{pn}}(n) \mid^{2}]=R_{\tilde{x},\text{pn}}(k,0) \\ &=\int_{-f_{\text{cut-off}}}^{f_{\text{cut-off}}} S_{\tilde{x}}(k,f)\otimes S_{p}(k,f))df \end{array} $$

(32)

Similarly, the conditional auto-correlation of $\tilde {z}_{k}(n)$ in the last line of (12) can be written as

$$\begin{array}{@{}rcl@{}} R_{\tilde{z}|\mathbf{\Theta}}(k,m)&=E\left[ \tilde{z}_{k}(n)\tilde{z}_{k}^{*}(n-m)|\mathbf{\Theta}\right] \\ &=b(n)\otimes b^{*}(n-m)\otimes \Big(\\ &\theta(k-1)R_{\tilde{x}}(k-1,m)R_{p}(m)e^{j2\pi (f_{k-1}-f_{k}) m} \\ &+\theta(k+1)R_{\tilde{x}}(k-1,m)R_{p}(m)e^{j2\pi (f_{k+1}-f_{k}) m}\Big) \\ &=\theta(k-1)\int_{-f_{\text{cut-off}}}^{f_{\text{cut-off}}} \big(S_{\tilde{x}}(k-1,f-f_{k-1}+f_{k})\\ &\otimes S_{p}(k,f)\big)e^{j2\pi f m}df \\ &+\theta(k+1)\int_{-f_{\text{cut-off}}}^{f_{\text{cut-off}}} \big(S_{\tilde{x}}(k+1,f-f_{k+1}+f_{k})\\ &\otimes S_{p}(k,f)\big)e^{j2\pi f m}df \end{array} $$

(33)

Again noting that the sampling rate does not alter the variance, we have

$$\begin{array}{@{}rcl@{}} \sigma_{z|\mathbf{\Theta}}^{2}(k)&=E\left[ \mid z_{k}(n) \mid^{2} \mathbf{\Theta}\right]=R_{\tilde{z}|\mathbf{\Theta}}(k,0) \\ &=\theta(k-1)\int_{- f_{\text{cut-off}}}^{f_{\text{cut-off}}} \big(S_{\tilde{x}}(k-1,f-f_{k-1}+f_{k}) \\ &\otimes S_{p}(f)\big) df \\ &+\theta(k+1)\int_{- f_{\text{cut-off}}}^{f_{\text{cut-off}}}\big(S_{\tilde{x}}(k+1,f-f_{k+1}+f_{k}) \\ &\otimes S_{p}(f)\big) df \end{array} $$

(34)

Spectral density expression in Eq. (30) by merely shifting the spectral density in frequency axis with the corresponding amount.

Apparently both (32) and (34) require the evaluation of similar type of integrals. Hence, we will present the solution for the general case which can then be evaluated for the special cases. The convolution in the integrand has the form $Q(f)=S_{\tilde {x}}(k,f-f_{o}) \otimes S_{p}(f)$ which can be expressed as

$$\begin{array}{@{}rcl@{}} Q(f)&=\int_{f_{o}-f_{\text{cut-off}}}^{f_{o}+f_{\text{cut-off}}} A_{k}S_{p}(f-f^{\prime})df^{\prime} \\ &=\frac{A_{k}}{\pi}\big(\tan^{-1}\left(\eta \tan(\pi (f-(f_{o}+f_{\text{cut-off}})))\right) \\ &-\text{tan}^{-1}\left(\eta \text{tan}(\pi (f-(f_{o}-f_{\text{cut-off}})))\right)\big) \end{array} $$

(35)

where η = (a +1)/(a−1) and f _o is a constant. In evaluating the integrand in (32), f _o = 0 whereas it takes the values f _{k −1}−f _k or f _{k +1}−f _k for the integrands in (34). Based on the last line of (35), we need to integrate the integrands of the form $\text {tan}^{-1}\left (\eta \text {tan}(\pi (f-f_{o}^{\prime }))\right )$ with respect to f where $f_{o}^{\prime }$ is another constant taking either the value of f _o + f _cut-off or f _o −f _cut-off. By denoting $u=\pi(f-f_o')$, $f^{\text{up}}=\pi(f_{\text{cut-off}}-f_o')$ and $f^{\text{low}}=\pi(-f_{\text{cut-off}}-f_o')$ , this integral can be evaluated as

$$\begin{array}{@{}rcl@{}} I(f_{o}') &= \int_{-f_{\text{cut-off}}}^{f_{\text{cut-off}}}\tan^{-1}(\eta \text{tan}(\pi (f-f_{o}')))df \nonumber \\&=B(f_{o}')-\frac{\eta}{\pi}\int_{-f_{\text{low}}}^{f^{\text{up}}}\frac{u}{\cos^{2}(u)+\eta^{2}\sin^{2}(u)}du \nonumber \\&=B(f_{o}')-\frac{\eta}{\pi}\int_{-f_{\text{low}}}^{f_{\text{up}}}\frac{u}{1-(1-\eta^{2})\sin^{2}(u)}du\nonumber \\&\approx B(f_{o}')-\frac{\eta}{\pi}\int_{-f_{\text{low}}}^{f_{\text{up}}}\frac{u}{1+\eta^{2}\sin^{2}(u)}du&\approx B(f_{o}')-\frac{\eta}{\pi}\int_{-f_{\text{low}}}^{f_{\text{up}}}\frac{u}{1+\eta^{2}\sin^{2}(u)}du \end{array} $$

(36)

where the second line follows upon using the well-known identity $\cos ^{2}(x)+\sin ^{2}(x)=1$, the approximation in the third line holds for practical values of 3-dB bandwidth and the term $B(f_o')$obtained via integration by parts as

$$\begin{array}{@{}rcl@{}} B(f_{o}')&=\left(f_{\text{cut-off}}-f_{o}'\right)\tan^{-1}\left(\eta \tan\left(\pi\left(f_{\text{cut-off}}-f_{o}'\right)\right)\right) \nonumber \\&+\left(f_{\text{cut-off}}+f_{o}'\right)\tan^{-1}\left(\eta \tan\left(-\pi\left(f_{\text{cut-off}}+f_{o}'\right)\right)\right) \end{array} $$

(37)

Then, by applying integration by parts once more, the integral is solved as $I (f_{o}^{\prime })=B(f_{o}^{\prime })-C(f_{o}^{\prime })$ where

$$\begin{array}{@{}rcl@{}} C(f_{o}')&=\frac{1}{\eta}\Big(\left(f_{\text{cut-off}}+f_{o}'\right)\cot\left(\pi\left(f_{\text{cut-off}}+f_{o}'\right)\right) \nonumber \\&-\left(f_{\text{cut-off}}-f_{o}'\right)\cot\left(\pi\left(f_{\text{cut-off}}-f_{o}'\right)\right)\Big) \nonumber \\&-\frac{1}{\pi \eta}\big( \log\left(|-\sin\left(\pi\left(f_{\text{cut-off}}+f_{o}'\right)\right)|\right) \nonumber \\&+\log\left(|\sin\left(\pi\left(f_{\text{cut-off}}-f_{o}'\right)\right)\right) |\big) \end{array} $$

(38)

After having derived the general solution, now we can explicitly write the analytic expressions for the integrals in (32) and (34) as

$$ \sigma_{x,\text{pn}}^{2}(k)=\frac{A_{k}}{\pi}\left(I\left(f_{\text{cut-off}}\right)-I\left(-f_{\text{cut-off}}\right)\right) $$

(39)

$$\begin{array}{@{}rcl@{}} \sigma_{z|\mathbf{\Theta}}^{2}&= \theta(k-1)\frac{A_{k-1}}{\pi}\big(I\left(f_{k-1}-f_{k}+f_{\text{cut-off}}\right) \\ &-I\left(f_{k-1}-f_{k}-f_{\text{cut-off}}\right)\big) \\ &+\theta(k+1)\frac{A_{k+1}}{\pi}\big(I\left(f_{k+1}-f_{k}+f_{\text{cut-off}}\right) \\ &-I\left(f_{k+1}-f_{k}-f_{\text{cut-off}}\right)\big) \end{array} $$

(40)

Although it is not immediate from the expression (39), considering that the typical 3-dB bandwidths of the oscillator process is much narrower compared to the actual bandwidth of the signal and most of the unit energy is concentrated within this 3-dB bandwidth, then we can approximate (39), i.e., $\sigma _{x,\text {pn}}^{2}(k) \approx {\sigma _{x}^{2}}(k)$. Acknowledgements If you’d like to thank anyone, place your comments here and remove the percent signs.