Abstract
This paper investigates a new secure relaying scheme, namely physical layer network coding based modify-and-forward (PMF), in which a relay node linearly combines the decoded data sent by a source node with an encrypted key before conveying the mixed data to a destination node. We first derive the general expression for the generalized secrecy outage probability (GSOP) of the PMF scheme and then use it to analyse the GSOP performance of various relaying and direct transmission strategies. The GSOP performance comparison indicates that these transmission strategies offer different advantages depending on the channel conditions and target secrecy rates, and relaying is not always desirable in terms of secrecy. Subsequently, we develop an opportunistic secure transmission protocol for cooperative wireless relay networks and formulate an optimisation problem to determine secrecy rate thresholds (SRTs) to dynamically select the optimal transmission strategy for achieving the lowest GSOP. The conditions for the existence of the SRTs are derived for various channel scenarios.












Similar content being viewed by others
Notes
This work is extended from [31, 32] where only results of the classical SOP were provided for the PMF scheme in the scenario that the eavesdropper can overhear the message in the first time slot, but does not attempt to decode the message from the relay due to its lack of knowledge of the modification process at the relay. We now take a further step by providing a detailed analysis for deriving the GSOP of the PMF scheme to link the concept of physical layer security and cryptography. Also, this work considers the general scenario when the eavesdropper can overhear and attempts to decode the message from both the source and the relay.
The encrypted key in the proposed scheme is generated at the physical layer as a training sequence. The design of a physical layer encryption scheme can be referred to in [33].
Note that a trusted relay channel is considered in this work where the relay can decode the confidential message prior to processing and forwarding it to the destination. The scenario of untrusted relay channels can be coped with by applying modulo-and-forward scheme at the relay with nested lattice encoding at the source as in [37].
Note that the above claim in Remark 6 is not applied for the case of the PMF-imperfect scheme, which will be verified in the numerical results. Although no conclusion can be straightforwardly drawn for the PMF-imperfect scheme, it is worth claiming an enhanced security achieved with the proposed PMF scheme since the shared knowledge of signaling information between the legitimate users is normally guaranteed by a dedicated channel. For completeness, in this work, we consider both imperfectly and perfectly shared knowledge between legitimate users in the PMF scheme.
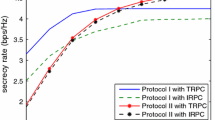
Note that the MF scheme always provides a lower GSOP compared to the DF and PMF schemes. Also, the GSOP of the PMF-imperfect scheme is always higher than that of the PMF-perfect scheme. Therefore, in what follows, we only discuss the PMF-perfect scheme (say PMF in short) with respect to DT, DF and CJ schemes, while the performance of the PMF-imperfect and MF schemes is only plotted for completeness, but not repeatedly interpreted for their reasoning.
References
Poor HV, Schaefer RF (2017) Wireless physical layer security. Proc Natl Acad Sci 114(1):19–26
Bassily R, Ekrem E, He X, Tekin E, Xie J, Bloch M, Ulukus S, Yener A (2013) Cooperative security at the physical layer: A summary of recent advances. IEEE Signal Process Mag 30(5):16–28
Fan L, Lei X, Duong TQ, Elkashlan M, Karagiannidis GK (2014) Secure multiuser communications in multiple amplify-and-forward relay networks. IEEE Trans Commun 62(9):3299–3310
Rodriguez LJ, Tran NH, Duong TQ, Le-Ngoc T, Elkashlan M, Shetty S (2015) Physical layer security in wireless cooperative relay networks: State of the art and beyond. IEEE Commun Mag 53(12):32–39
Fan L, Lei X, Yang N, Duong TQ, Karagiannidis GK (2016) Secure multiple amplify-and-forward relaying with cochannel interference,”. IEEE J Sel Topics Signal Process 10(8):1494–1505
Nasir AA, Tuan HD, Duong TQ, Poor HV (2017) Secure and energy-efficient beamforming for simultaneous information and energy transfer. IEEE Trans Wireless Commun 16(11):7523– 7537
Sendonaris A, Erkip E, Aazhang B (2003) User cooperation diversity - Part I. System description. IEEE Trans Commun 51(11):1927–1938
Laneman J, Tse D, Wornell G (2004) Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans Inf Theory 50(12):3062–3080
Shannon C (1949) Communication theory of secrecy systems. Bell Syst Tech J 28(4):656–715
Wyner A (1975) The wire-tap channel. Bell Syst Tech J 54(8):1355–1387
Vilela J, Bloch M, Barros J, McLaughlin S (2011) Wireless secrecy regions with friendly jamming. IEEE Trans Inf Forensics Security 6(2):256–266
Krikidis I, Thompson J, Mclaughlin S (2009) Relay selection for secure cooperative networks with jamming. IEEE Trans Wireless Commun 8(10):5003–5011
Liu Y, Li J, Petropulu AP (2013) Destination assisted cooperative jamming for wireless physical-layer security. IEEE Trans Inf Forensics Security 8(4):682–694
Tekin E, Yener A (2008) The general gaussian multiple-access and two-way wiretap channels: Achievable rates and cooperative jamming. IEEE Trans Inf Theory 54(6):2735–2751
Tekin E (2008) The Gaussian multiple access wire-tap channel. IEEE Trans Inf Theory 54(12):5747–5755
Liu Y, Petropulu AP, Poor HV (2011) Joint decode-and-forward and jamming for wireless physical layer security with destination assistance. In: Proc ASILOMAR 2011. Pacific Grove, USA, pp 109–113
Lai L, El Gamal H (2008) The relay-eavesdropper channel: Cooperation for secrecy. IEEE Trans Inf Theory 54(9):4005–4019
Bassily R, Ulukus S (2013) Deaf cooperation and relay selection strategies for secure communication in multiple relay networks. IEEE Trans Signal Process 61(6):1544–1554
Ahlswede R, Cai N, Li S-Y, Yeung R (2000) Network information flow. IEEE Trans Inf Theory 46(4):1204–1216
Koetter R, Medard M (2003) An algebraic approach to network coding. IEEE/ACM Trans Netw 11 (5):782–795
Zhang S, Liew SC, Lam PP (2006) Hot topic: Physical-layer network coding. In: Proc ACM MobiCom’06, Los Angeles, CA, USA, pp 358–365
Vien Q -T, Nguyen HX, Stewart BG, Choi J, Tu W (2015) On the energy-delay tradeoff and relay positioning of wireless butterfly networks. IEEE Trans Veh Technol 64(1):159–172
Vien Q-T, Stewart BG, Tianfield H, Nguyen HX (2013) Cooperative retransmission for wireless regenerative multirelay networks. IEEE Trans Veh Technol 62(2):735–747
Vien Q-T, Nguyen HX, Choi J, Stewart BG, Tianfield H (2012) Network coding-based block acknowledgement scheme for wireless regenerative relay networks. IET Commun 6(16):2593–2601
Vien Q-T, Tran L-N, Hong E-K (2011) Network coding-based retransmission for relay aided multisource multicast networks. EURASIP J Wireless Commun Netw 2011(643920):10
Cui T, Ho T, Kliewer J (2013) On secure network coding with nonuniform or restricted wiretap sets. IEEE Trans Inf Theory 59(1):166–176
Cai N, Yeung R (2011) Secure network coding on a wiretap network. IEEE Trans Inf Theory 57(1):424–435
Gabry F, Thobaben R, Skoglund M (2011) Outage performances for amplify-and-forward, decode-and-forward and cooperative jamming strategies for the wiretap channel. In: Proc IEEE WCNC’11, Cancun, Mexico, pp 1328–1333
Bassily R, Ulukus S (2012) Secure communication in multiple relay networks through decode-and-forward strategies. J Commun and Netw 14(4):352–363
Kim SW (2014) Modify-and-forward for securing cooperative relay communications. In: International zurich seminar on communications (IZS), Zurich, Switzerland, pp 136–139
Vien Q-T, Le TA, Nguyen HX, Phan H (2016) A secure network coding based modify-and-forward scheme for cooperative wireless relay networks. In: Proc IEEE VTC 2016-Spring, Nanjing, China, pp 1–5
Vien Q-T, Le TA, Duong TQ (2017) Opportunistic secure transmission for wireless relay networks with modify-and-forward protocol. In: Proc IEEE ICC, 2017, Paris, France, pp 1–6
Zhang J, Marshall A, Woods R, Duong TQ (2017) Design of an OFDM physical layer encryption scheme. IEEE Trans Veh Technol 66(3):2114–2127
He B, Zhou X, Swindlehurst AL (2016) On secrecy metrics for physical layer security over quasi-static fading channels. IEEE Trans Wireless Commun 15(10):6913–6924
Baldi M, Chiaraluce F, Laurenti N, Tomasin S, Renna F (2014) Secrecy transmission on parallel channels: Theoretical limits and performance of practical codes. IEEE Trans Inf Forensics Security 9(11):1765–1779
Barros J, Rodrigues M (2006) Secrecy capacity of wireless channels. In: Proc IEEE ISIT’06, Seattle, WA, USA, pp 356–360
Zhang S, Fan L, Peng M, Poor HV (2016) Near-optimal modulo-and-forward scheme for the untrusted relay channel. IEEE Trans Inf Theory 62(5):2545–2556
Smith G (2011) Quantifying information flow using min-entropy. In: Proc QEST, 2011 Aachen, Germany, pp 159–167
Simon MK, Alouini M-S (2005) Digital communication over fading channels, 2nd edn. Wiley, New York
Gradshteyn IS, Ryzhik IM (2007) Table of integrals, series, and products, Academic Press, Cambridge
Papoulis A (2002) Probability, random variables, and stochastic processes, 4th edn. Mc-Graw Hill, New York
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Proof of Lemma 1
Given \(Y=\frac {a^{2}X}{b^{2}X + 1}\) and X = c|Z|2 where c is a positive constant, it can be deduced that a2 ≥ b2Y. The cdf of Y can be computed by [41]
Note that the pdf and cdf of X are given by
respectively. Substituting Eq. 44 into Eq. 42, we have
The pdf of Y can be therefore obtained by
Appendix B: Proof of Theorem 1
For brevity, let \(X=\gamma _{\mathcal {SR}}\), \(Y=\gamma _{\mathcal {SD}}\), \(Z=\gamma _{\mathcal {RD}}\), \(U=\gamma _{\mathcal {SE}}\) and \(V=\gamma _{\mathcal {RE}}\). We can rewrite Eq. 14 as
Note that the secure communication is possible with a positive secrecy capacity if the legitimate links, including the direct and/or relaying links, have higher channel gains over the eavesdropper links. In order to prevent the secrecy outage from always happening, it is assumed that min{X, Y + Z} > U + V. From Eq. 47, we have
Considering two scenarios of X ≤ Y + Z and X > Y + Z, Eq. 48 can be rewritten by Eq. 49 (see the top of next page).
Deriving P1 and P2 in Eq. 49, it can be observed that, if \(X\leqslant \min \{Y,2^{2 \theta R_{s}}-1\}\), then \(\Pr \{2^{-2 \theta R_{s}}(1+X)-1<U+V<X\}= 1\) and Pr{X ≤ Y + Z} = 1 since \(U+V\geqslant 0\) and \(Z\geqslant 0\). This means P1 = 1 and P2 = 0, i. e. \(P_{out}^{(PMF)}= 1\) (outage occurs). Similarly, if \(Y+Z\leqslant \min \{X,2^{2 \theta R_{s}}-1\}\), then \(\Pr \{2^{-2 \theta R_{s}}(1+Y+Z)-1<U+V<Y+Z\}= 1\) and Pr{X > Y + Z} = 1 since \(U+V\geqslant 0\), and thus outage happens. Therefore, in order to avoid the outage, by considering all these above conditions, we can arrive at Eqs. 50 and 51 (see the top of next page).
For simplicity, let us define
Substituting Eqs. 50 and 51 into Eq. 49 with I1(x) and I2(x), the theorem is proved.
Appendix C: Proof of Proposition 1
From \(\frac {d f(x)}{d x}>\frac {d g(x)}{d x}>0\), there exist x1 > 0 and x2 > 0 such that
If f(0) < g(0), then there exists a crossing point x′ = x1 = x2 > 0 such that f(x′) = g(x′) and thus (f(x′) − f(0))/x′ > (g(x′) − g(0))/x′ satisfying Eq. 54. Conversely, if there exists a crossing point x′ = x1 = x2 > 0 satisfying Eq. 54, then we can easily deduce that f(0) < g(0).
Proof of uniqueness: Let us assume that there exists 0 < x″ ≠ x′ satisfying f(x″) = g(x″) and f(x′) = g(x′). We have
which contradicts the fact that \(\frac {d f(x)}{d x}>\frac {d g(x)}{d x}\).
Therefore, we can conclude that ∃!x′ > 0 : f(x′) = g(x′) if and only if f(0) < g(0).
Appendix D: Proof of Theorem 2
In the DT protocol, as Rs → 0, it can be observed from Eq. 26 that
In the RT protocol, as Rs → 0, Φ(x) in Eq. 37 approaches
Substituting Eq. 57 into Eq. 36, the limit of \(P^{(RT)}_{out}\) can be obtained by Eq. 58.
Denote \({\Delta }=P^{(RT)}_{0}-P^{(DT)}_{0}\). Solving Δ < 0, after some mathematical manipulations, we obtain the condition of the channel quality of various links as in Eq. 59.
It can be seen that, if \(\bar {\gamma }_{\mathcal {SD}}\bar {\gamma }_{\mathcal {SE}}<\bar {\gamma }^{2}_{\mathcal {SR}}\), \(\bar {\gamma }_{\mathcal {SD}}<\sqrt {\bar {\gamma }_{\mathcal {SR}}\bar {\gamma }_{\mathcal {SE}}/2}\) and \(\bar {\gamma }_{\mathcal {SD}}<\sqrt {\bar {\gamma }_{\mathcal {SR}}\bar {\gamma }_{\mathcal {RD}}/2}\), then Δ < 0, i.e. \(P^{(RT)}_{0}<P^{(DT)}_{0}\). Additionally, as in the conventional relaying scheme, the gradient of the GSOP performance of the RT scheme is higher than that of the DT scheme and the GSOP of both schemes increases as a function of the target secrecy rate, i.e. \(\frac {dP^{(RT)}_{out}}{dR_{s}}>\frac {dP^{(DT)}_{out}}{dR_{s}}>0\). Therefore, from Proposition 1, we can conclude that \(\exists ! R^{\prime }_{s}>0: P^{(DT)}_{out}(R^{\prime }_{s})=P^{(RT)}_{out}(R^{\prime }_{s})\).
Rights and permissions
About this article
Cite this article
Vien, QT., Le, T.A., Nguyen, H.X. et al. A Physical Layer Network Coding Based Modify-and-Forward with Opportunistic Secure Cooperative Transmission Protocol. Mobile Netw Appl 24, 464–479 (2019). https://doi.org/10.1007/s11036-018-1157-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11036-018-1157-1