Energy functional driven by multiple features for brain lesion segmentation

Abstract

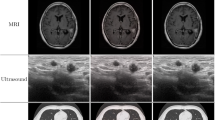
Brain lesion segmentation can provide useful information for diagnosis and treatment planning. The extracted features are beneficial to the accuracy of brain lesion segmentation. However, due to complex structures of different tissues in different brain modalities, i.e., magnetic resonance imaging (MRI) and computed tomography (CT), the extraction of useful features is a challenging task. In this paper, the effectiveness of four different features, i.e., local intensity, shape, and area to discriminate brain lesion from other normal tissues is explored. Here, the performance of each feature in brain images is analyzed. Next, an energy functional framework integrated with multiple features is implemented. The experiments show that the proposed method can perform well in both real MRI brain tumor and other CT encephalorrhagia segmentation obtained from Quzhou People’s hospital. The concrete innovations are as follows: (1) in view of the complexity of brain imaging and the difficulty of identifying lesion region, the proposed method can be applied to the segmentation of more complex brain lesions; (2) multiple features, i.e., local intensity, shape, and area are extracted to construct the proposed energy functional; (3) the proposed model is demonstrated using 32 real MRI images from ten pediatric patients and three different similarity metrics are evaluated. To verify the performance of the proposed algorithm, more than representative 20 images are randomly selected in databases of Quzhou People’s hospital for evaluation. The average DICE coefficient, the Jaccard (JAC) distance, the Recall, and Root Mean Square Error (RMSE) are 0.95, 0.90, 0.92, and 0.07, respectively. The proposed method can reach better accuracy performance than the traditional energy functional-based methods and other state-of-the-art brain lesion segmentation methods.

Appendices

6. Appendix A

Modeling of the proposed energy functional (10) and its solution. According to the gradient descent method, the proposed energy functional is defined as:

$$\begin{gathered} \frac{\partial \varphi }{{\partial t}} = - \frac{\partial E\left( \varphi \right)}{{\partial \varphi }} \\ = - \left( {\frac{{\partial E_{J} \left( \varphi \right)}}{\partial \varphi } + \frac{{\partial E_{A} \left( \varphi \right)}}{\partial \varphi } + \frac{{\partial E_{S} \left( \varphi \right)}}{\partial \varphi }} \right) \\ \end{gathered}$$

(13)

Each term used here is defined. For convenience, let

$$Den_{1} = \int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * H\left( {\varphi \left( {x,y} \right)} \right)dx} dy$$

(14)

and

$$Den_{2} = \int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left( {1{ - }H\left( {\varphi \left( {x,y} \right)} \right)} \right)dx} dy$$

(15)

$$Num_{1} = \int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)H\left( {\varphi \left( {x,y} \right)} \right)} \right]dx} dy$$

(16)

and

$$Num_{2} = \int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)\left( {{1 - }H\left( {\varphi \left( {x,y} \right)} \right)} \right)} \right]dx} dy$$

(17)

Then, we can get:

$$\begin{gathered} J_{1} = \frac{{Num_{1} }}{{Den_{1} }} \\ = \frac{{\int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)H\left( {\varphi \left( {x,y} \right)} \right)} \right]dx} dy}}{{\int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * H\left( {\varphi \left( {x,y} \right)} \right)dx} dy}} \\ { = }\frac{{W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)H\left( {\varphi \left( {x,y} \right)} \right)} \right]}}{{W\left( {I_{x,y}^{C} ,r} \right) * H\left( {\varphi \left( {x,y} \right)} \right)}} \\ \end{gathered}$$

(18)

and

$$\begin{gathered} J_{2} = \frac{{Num_{2} }}{{Den_{2} }} \\ = \frac{{\int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)\left( {1{ - }H\left( {\varphi \left( {x,y} \right)} \right)} \right)} \right]dx} dy}}{{\int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left( {1{ - }H\left( {\varphi \left( {x,y} \right)} \right)} \right)dx} dy}} \\ { = }\frac{{W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)\left( {1{ - }H\left( {\varphi \left( {x,y} \right)} \right)} \right)} \right]}}{{W\left( {I_{x,y}^{C} ,r} \right) * \left( {1{ - }H\left( {\varphi \left( {x,y} \right)} \right)} \right)}} \\ \end{gathered}$$

(19)

To solve the above equation, the following partial derivatives need to be calculated firstly:

$$\begin{gathered} \frac{{\partial J_{1} }}{\partial \varphi } = \frac{{Num_{1}^{\prime } Den_{1} - Num_{1} Den_{1}^{\prime } }}{{Den_{1}^{2} }} = \frac{{Num_{1}^{\prime } - J_{1} Den_{1}^{\prime } }}{{Den_{1} }} \\ = \frac{{\int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)\delta \left( {\varphi \left( {x,y} \right)} \right)} \right]dx} dy - J_{1} \int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \delta \left( {\varphi \left( {x,y} \right)} \right)dx} dy}}{{\int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * H\left( {\varphi \left( {x,y} \right)} \right)dx} dy}} \\ = \frac{{W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)\delta \left( {\varphi \left( {x,y} \right)} \right)} \right] - J_{1} \left[ {W\left( {I_{x,y}^{C} ,r} \right) * \delta \left( {\varphi \left( {x,y} \right)} \right)} \right]}}{{W\left( {I_{x,y}^{C} ,r} \right) * H\left( {\varphi \left( {x,y} \right)} \right)}} \\ \end{gathered}$$

(20)

and

$$\begin{gathered} \frac{{\partial J_{2} }}{\partial \varphi } = \frac{{Num_{2}^{\prime } Den_{2} - Num_{2} Den_{2}^{\prime } }}{{Den_{2}^{2} }} = \frac{{Num_{2}^{\prime } - J_{2} Den_{2}^{\prime } }}{{Den_{2} }} \\ = \frac{{ - \int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)\left( {1{ - }\delta \left( {\varphi \left( {x,y} \right)} \right)} \right)} \right]dx} dy + J_{2} \int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left( {{\mathbf{1}}{ - }\delta \left( {\varphi \left( {x,y} \right)} \right)} \right)dx} dy}}{{\int_{\Omega } {W\left( {I_{x,y}^{C} ,r} \right) * \left( {{\mathbf{1}}{ - }H\left( {\varphi \left( {x,y} \right)} \right)} \right)dx} dy}} \\ = - \frac{{W\left( {I_{x,y}^{C} ,r} \right) * \left[ {I\left( {x,y} \right)\left( {1{ - }\delta \left( {\varphi \left( {x,y} \right)} \right)} \right)} \right] - J_{2} \left[ {W\left( {I_{x,y}^{C} ,r} \right) * \left( {{\mathbf{1}}{ - }\delta \left( {\varphi \left( {x,y} \right)} \right)} \right)} \right]}}{{W\left( {I_{x,y}^{C} ,r} \right) * \left( {{\mathbf{1}}{ - }H\left( {\varphi \left( {x,y} \right)} \right)} \right)}} \\ \end{gathered}$$

(21)

where ${\mathbf{1}}$ denotes a constant matrix with value 1;

So

$$\begin{gathered} \frac{{\partial E_{J} }}{\partial \varphi }{ = }2\left[ {\left( {I\left( {x,y} \right) - J_{1} \left( {W,c} \right)} \right) \cdot \frac{{\partial J_{1} }}{\partial \varphi }{ - }\left( {I\left( {x,y} \right) - J_{2} \left( {W,c} \right)} \right) \cdot \frac{{\partial J_{2} }}{\partial \varphi }} \right] \hfill \\ { = }2\left[ {\left( {I\left( {x,y} \right) - J_{1} \left( {W,c} \right)} \right) \cdot \frac{{W * \left( {I\delta } \right) - J_{1} \left( {W * \delta } \right)}}{W * H}{ + }\left( {I\left( {x,y} \right) - J_{2} \left( {W,c} \right)} \right) \cdot \frac{{W * \left( {I\left( {{\mathbf{1}} - \delta } \right)} \right) - J_{2} \left( {W * \left( {{\mathbf{1}} - \delta } \right)} \right)}}{{W * \left( {{\mathbf{1}} - H} \right)}}} \right] \hfill \\ \end{gathered}$$

(22)

Here, the parameters of some variables, i.e., $W$, $I$, $H$, and $\delta$ have been omitted to make them more descriptive.

Besides, by the interpretation of Euler Lagrange and integration, we get

$$\frac{{\partial E_{S} }}{\partial \varphi } = 2\delta \left( \varphi \right)\left( {Z_{1} H\left( \varphi \right) - Z_{2} \left( {1 - H\left( \varphi \right)} \right)} \right)\left( {Z_{1} + Z_{2} } \right)$$

(23)

and

$$\frac{{\partial E_{A} }}{\partial \varphi } = \delta \left( \varphi \right)$$

(24)

Theorem 1.

The proposed energy functional (10) is uniformly bounded in Sobolev space $W^{k,p} \left( \Omega \right)$.

Theorem 2.

The convergence value is the minimum in the energy functional (10).

Proof.

From Theorem 1, there exists a minimal sequence ${\lbrace} \varphi_{n} {\rbrace} \in W^{k,p} \left( \Omega \right),n \in N$. By the property of Sobolev Space $W^{k,p} \left( \Omega \right)$, one can get that there exists a convergent subsequence $\varphi_{n}$ that converges to $\varphi$, that is $\varphi_{n} \to \varphi$.

Appendix B

Theorem 1.

The proposed energy functional (10) is uniformly bounded in Sobolev space $W^{k,p} \left( \Omega \right)$.

Theorem 2.

The convergence value is the minimum in the energy functional (10).

Proof.

From Theorem 1, there exists a minimal sequence ${\lbrace}\varphi_{n} {\rbrace} \in W^{k,p} \left( \Omega \right),n \in N$. By the property of Sobolev Space $W^{k,p} \left( \Omega \right)$, one can get that there exists a convergent subsequence $\varphi_{n}$ that converges to $\varphi$, that is $\varphi_{n} \to \varphi$.

Let $\Omega \to R$ be the bounded open subset, and $\xi$ denote the integrable function in Sobolev space $W^{k,p} \left( \Omega \right)$ (Sobolev space is defined as a vector space of functions equipped with a kp -norm). Then, the energy functional (10) is set as:

$$\begin{gathered} \xi { = }\sup {\lbrace}\left. {\int {\left( {E_{J} \left( \varphi \right) + E_{A} \left( \varphi \right) + E_{S} \left( \varphi \right)} \right) \cdot \nabla \varphi d\Omega } } \right|\varphi \\ = \left( {\varphi_{1} ,\varphi_{2} , \cdots ,\varphi_{N} } \right) \in W^{0,1} \left( \varphi \right)^{N} ,|\varphi |_{{W^{\infty } \left( \Omega \right)}} < 1{\rbrace } \\ \end{gathered}$$

(25)

where $N$ is the maximum iteration of the level set $\varphi$, $d\Omega$ is the Lebesgue measure $\Omega = \sup {{\lbrace}\Omega_{\varphi > 0} ,\Omega_{\varphi < 0} {\rbrace}}$, and

$$\nabla \varphi = \sum\limits_{i = 1}^{N} {\frac{{\partial \varphi_{i} }}{{\partial x_{i} }}}$$

(26)

Then, one can get that $\xi \in W\left( \Omega \right)$, $\nabla \xi \in W^{0,1} \left( \Omega \right)$, i.e.,

$$- \int {\left( {E_{J} \left( \varphi \right) + E_{A} \left( \varphi \right) + E_{S} \left( \varphi \right)} \right) \cdot \nabla \varphi d\Omega } = \int {\left( {\nabla \left( {E_{J} \left( \varphi \right) + E_{A} \left( \varphi \right) + E_{S} \left( \varphi \right)} \right)} \right) \cdot \varphi d\Omega }$$

(27)

and the corresponding bounded variation space $BV\left( \Omega \right)$ is

$$BV\left( \Omega \right){ = }\left\{ {\left. \varphi \right|\varphi \in W^{0,1} \left( \Omega \right)} \right\}$$

(28)

By the characteristics of the space $BV\left( \Omega \right)$, we can get that if $\varphi \in BV\left( \Omega \right)$, then

$$\xi \left( {E_{J} ,E_{A} ,E_{S} } \right) = \int_{ - \infty }^{ + \infty } {W^{0,1} \left( {\partial \Omega_{\sigma } } \right)} d\sigma$$

(29)

Here, $\partial \Omega_{\sigma }$ is the boundary and $W^{0,1} \left( {\partial \Omega_{\sigma } } \right)$ denotes the length of $\partial \Omega_{\sigma }$.

In conclusion, the proposed energy functional (10) is uniformly bounded in the Sobolev space $W^{k,p} \left( \Omega \right)$.

Appendix C

Theorem 2.

The convergence value is the minimum in the energy functional (10).

Proof.

From Theorem 1, there exists a minimal sequence ${\lbrace}\varphi_{n} {\rbrace} \in W^{k,p} \left( \Omega \right),n \in N$. By the property of Sobolev Space $W^{k,p} \left( \Omega \right)$, one can get that there exists a convergent subsequence $\varphi_{n}$ that converges to $\varphi$, that is $\varphi_{n} \to \varphi$.

For the first item $E_{J}$, by the properties of the uniform boundedness and the lower semicontinuous of the norm,

$$E_{J}^{ + } = \left( {I\left( {x,y} \right) - J_{1} \left( {W,c} \right)} \right) \le M_{1}$$

(30)

and

$$E_{J}^{ - } = \left( {I\left( {x,y} \right) - J_{2} \left( {W,c} \right)} \right) \le M_{2}$$

(31)

Consider that the characteristics of the window function $W$ and the average intensities $\left\{ {J_{1} ,J_{2} } \right\}$, we can get that

$$\frac{{W * \left( {I\delta } \right) - J_{1} \left( {W * \delta } \right)}}{W * H} \le M_{3}$$

(32)

and

$$\frac{{W * \left( {I\left( {{\mathbf{1}} - \delta } \right)} \right) - J_{2} \left( {W * \left( {{\mathbf{1}} - \delta } \right)} \right)}}{{W * \left( {{\mathbf{1}} - H} \right)}} \le M_{4}$$

(33)

where $M_{i} ,i = 1, \cdots ,4$ are constants. For the other items, by the mandatory of the function $\delta \left( \varphi \right) \cdot V$ ($V$ is a constant) and taking the characteristics of the function $E_{A}$ ($V = Z_{1} H\left( \varphi \right) - Z_{2} \left( {1 - H\left( \varphi \right)} \right)$) and $E_{S}$ ($V = 1$) into account: $\partial E_{A} \left( \varphi \right) \le M$, $\partial E_{s} \left( \varphi \right) \le N$. Here, $M$ and $N$ are constants. In addition, BV space is compact, so $\varphi_{n}$ is convergent to $\varphi$. By Fatou’s lemma, we can get: $\varphi \le \mathop {\lim }\limits_{n \to \infty } \inf \varphi_{n}$, and $\varphi$ convergences and there exists a minimum. Therefore, the energy functional (10) is uniformly bounded, convergences and there exists a minimum.