Boundedness analysis for open Chemical Reaction Networks with mass-action kinetics

Abstract

This paper describes the working principles of an algorithm for boundedness analysis of open Chemical Reaction Networks endowed with mass-action kinetics. Such models can be thought of both as a special class of compartmental systems or a particular type of continuous Petri Nets, in which the firing rates of transitions are not constant or preassigned, but expressed as a function of the continuous marking of the network (function which in chemistry is referred to as the “kinetics”). The algorithm can be applied to a broad class of such open networks, and returns, as an outcome, a classification of the possible dynamical behaviors that are compatible with the network structure, by classifying each variable either as bounded, converging to 0 or diverging to ∞. This can be viewed as a qualitative study of Input–Output Stability for chemical networks, or more precisely, as a classification of its possible I–O instability patterns. Our goal is to analyze the system irrespectively of values of kinetic parameters. More precisely, we attempt to analyze it simultaneously for all possible values. Remarkably, tests on non-trivial examples (one of which is discussed in this paper) showed that, as the kinetic constants of the network are varied, all the compatible behaviors could be observed in simulations. Finally, we discuss and illustrate how the results relate to previous works on the qualitative dynamics of closed reaction networks.

Appendices

A. Proof of technical lemmas

1.1 A.1 Proof of the main technical lemma

Consider a scalar linear time-varying system as in (9); it is well-known that its unique solution can be computed as:

$$ x(t) = e^{ - \int_T^t a(s) ds } x(T) + \int\limits_T^t e^{ - \int_s^t a(\tau) } d \tau b(s) ds. $$

(13)

The main technical lemma follows, on a case by case basis, by considering the following inequalities:

• 1. Let a(t) ∈ [ a _min, a _max ] for all t ≥ T and some a _min > 0; by virtue of (13) we have:

  $$ \begin{aligned} x(t)\,&\leq\,e^{-(t-T) a_{\min} } x(T) + \int\limits_T^t e^{- (t-s) a_{\min} } b(s) ds\\ x(t)\,&\geq\,e^{-(t-T) a_{\max} } x(T) + \int\limits_T^t e^{- (t-s) a_{\max} } b(s) ds. \end{aligned} $$

  (14)

  Assume next b(t) ∈ [b _min, b _max ], for some b _min > 0. Then, we may estimate x(t) as reported below:

  $$ \begin{aligned} x(t)\,&\leq\,e^{-(t-T) a_{\min} } x(T) + \int\limits_T^t e^{- (t-s) a_{\min} } b_{\max} ds\\ x(t)\,&\geq\,e^{-(t-T) a_{\max} } x(T) + \int\limits_T^t e^{- (t-s) a_{\max} } b_{\min} ds. \end{aligned} $$

  (15)

  Hence, for all t ≥ T we find:

  $$ x(t) \in \left [ \frac{b_{\min}}{ a_{\max} }, x(T) + \frac{b_{\max}}{a_{\min}} \right ]. $$

  Let us treat next the case b(t) → 0. Notice, first, that B _T : = max{b(t) : t ≥ T} also tends to 0 as T grows to infinity. Furthermore, by continuity of b(t), it holds B ₀ < +∞. Then, it is straightforward to prove boundedness of x(t) by virtue of (14):

  $$ x(t) \leq x(0) + \int\limits_0^t e^{- (t-s) a_{\min} } B_0 ds \leq x(0) + B_0 / a_{\min} < + \infty. $$

  Substituting this upper-bound again in the same equation allows to state:

  $$ x(t)\,\leq\,e^{-(t-T) a_{\min} } [x(0) + B_0/a_{\min} ] + \int\limits_T^t e^{- (t-s) a_{\min} } ds B_T $$

  so that, taking the limit, we obtain:

  $$ \limsup_{t \rightarrow + \infty} x(t)\,\leq\,B_T/ a_{\min} \qquad \forall T> 0 $$

  Now, by arbitrariness of T we may conclude $\lim_{t \rightarrow+\infty} x(t) =0$ as desired.

  The case, b(t) → +∞ can be treated in a symmetric way. Indeed, b _T : = min{b(t): t ≥ T} tends to +∞ as T grows unbounded. In turn, this allows to claim:

  $$ x(t) \geq \int\limits_T^t e^{- (t-s) a_{\max} } b_T ds $$

  which taking limits as t → +∞ yields

  $$ \liminf_{t \rightarrow + \infty} x(t) \geq \int\limits_T^{+ \infty} e^{- (t-s) a_{\max} } b_T = b_T / a_{\max}. $$

  Hence, by arbitrariness of T, and the fact that b _T → +∞ as T → +∞ we may conclude x(t)→ +∞ as t → +∞.

• 2. Let us consider next the case a(t) → +∞ as t→ +∞. We define a _T : = min{a(t): t ≥ T}. Clearly a _T → +∞ as T → +∞. Let b(t)  ∈ [0, b _max] for all t ≥ T. Then, we may estimate x(t) as follows:

  $$ x(t)\,\leq\,e^{- (t-T) a_T} x(T) + \int\limits_T^t e^{- \int_s^t a_T d \tau } b_{\max} ds. $$

  Letting t → +∞ we obtain for any T > 0:

  $$ \limsup_{t \rightarrow + \infty} x(t)\,\leq\,b_{\max} / a_T $$

  Indeed, by arbitrariness of T we may conclude x(t) →0 as t → +∞.

• 3. The only remaining case is a(t) → 0. Assume b(t)  ∈ [b _min +∞) for some b _min > 0. Indeed, we may consider the quantity a _T : = max{a(t): t ≥ T} and remark that a _T → 0 as T → +∞. Then, x(t) can be bounded from below as follows:

  $$ x(t) \geq \int\limits_T^t e^{- \int_s^t a_T d \tau } b_{\min} ds $$

  Let T > 0 be arbitrary and take the limit as t → +∞; this yields:

  $$ \liminf_{t \rightarrow + \infty} x(t) \geq b_{\min} / a_T. $$

  Hence, by arbitrariness of T, x(t) → +∞ as t→ +∞. This concludes the proof of the main technical Lemma.

B. Description of the algorithm

Efficient implementation of the algorithm is based on the selective exploration of the tree of all possible labelings and on efficient exclusion of branches which are to be found inconsistent, according to the standard principle of branch and bound depth search. Thanks to the connection with siphon’s computation discussed in Sect. 6, it can be seen as some non trivial extension of the algorithm described in Boer and Murata (1994) for the computation of minimal siphons, which however only uses 2 types of labels, 0 and 1, respectively for places which do belong and do not belong to the siphon currently being tested for. These are fairly complex algorithms, both computationally and in terms of the source code which is needed to implement them. Their description, to be intelligible, would require the space and accuracy of a stand-alone paper. We feel that is beyond the scope of the present paper, which mainly deals with the working principles of such an algorithm. For those interested in computational aspects though, it might be helpful to know that, rather than proceeding with the computation of all possible labelings and some a posteriori check of consistency, we gradually update the currently explored configuration by making use of set-valued labels, viz. labels corresponding to the following 7 different possibilities: 0, 1, ∞, 01, 1∞, 0∞, 01∞. Those involving more than one symbol are meant to be associated to variables for which more than one possible asymptotic behavior is still plausible and has to be simultaneously taken into account. The tree is explored thanks to a branch and bound technique which performs consistency checks all the way down from the root to the leaves. In such a way, incompatible labelings are discarded much earlier in the construction of the tree. Tables for addition and multiplication among such labels are constructed by trivially generalizing those for labels involving a single symbol in order to further speed up operations. Whenever consistency of a stage is tested, the tree is branched by splitting into 2 or 3 different cases, by attaching a single-valued label to one of the species that was still ambiguously marked. Then we proceed to recomputation of all the labels and to consistency check. Indeed the algorithm performed very rapidly on networks of reasonable size as the one included in this paper; for the example discussed here an answer was obtained in less than 3 s on a standard PC.

C. How to reproduce different scenarios

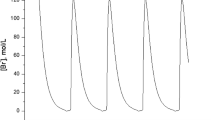
Hereby we provide parameters values which allow to reproduce the different scenarios exhibited by example (6). Initial conditions can always be picked to be simply [1, 1, 1, 1, 1, 1, 1, 1, 1]. See Table 6.

Table 6 Parameters values to reproduce in simulation the 4 possible scenarios