Skip to main content
SpringerLink
Log in

An Application of Generalized Fuzzy Hyperbolic Model for Solving Fractional Optimal Control Problems with Caputo–Fabrizio Derivative

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

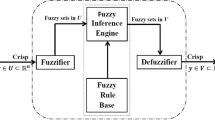
Abstract

In this paper we present a new approach for solving a class of fractional optimal control problems based on generalized fuzzy hyperbolic model. The fractional derivatives are described in the Caputo–Fabrizio sense. In order to solve this problem, the necessary optimality conditions associated to the fractional optimal control problem is first derived. The solution of these conditions is then approximated by fuzzy solution based on generalized fuzzy hyperbolic model. A learning algorithm is used to achieve the adjustable parameters of the obtained fuzzy solution. In order to confirm the efficiency and accuracy of the proposed approach, some illustrative examples are implemented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Sun H, Zhang Y, Baleanu D, Chen W (2018) Chen Y A new collection of real world applications of fractional calculus in science and engineering. Commun Nonlinear Sci Numer Simulat 64:213–231

    MATH  Google Scholar 

  2. Pham VT, Vaidyanathan S, Volos C, Kapitaniak T (2018) Nonlinear dynamical systems with self-excited and hidden attractors. Springer, Berlin

    MATH  Google Scholar 

  3. Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, New York

    MATH  Google Scholar 

  4. Riewe F (1996) Nonconservative Lagrangian and Hamiltonian mechanics. Phys Rev E 53(2):1890–1899

    MathSciNet  Google Scholar 

  5. Riewe F (1997) Mechanics with fractional derivatives. Phys Rev E 55(3):3582–3592

    MathSciNet  Google Scholar 

  6. Agrawal O (2004) A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn 38:323–337

    MathSciNet  MATH  Google Scholar 

  7. Bhrawy AH, Doha EH, Baleanu D, Ezz-Eldien SS, Abdelkawy MA (2015) An accurate numerical technique for solving fractional optimal control problems. Proc Roman Acad Ser A 16:47–54

    MathSciNet  MATH  Google Scholar 

  8. Bhrawy AH, Ezz-Eldien SS (2016) A new Legendre operational technique for delay fractional optimal control problems. Calcolo 53:521–543

  9. Bhrawy AH, Doha EH, Machado JA, Ezz-Eldien SS (2015) An efficient numerical scheme for solving multi-dimensional fractional optimal control problems with a quadratic performance index. Asian J Control 17(6):2389–2402

    MathSciNet  MATH  Google Scholar 

  10. Zaky MA (2018) A Legendre collocation method for distributed-order fractional optimal control problems. Nonlinear Dyn 91(4):2667–2681

    MATH  Google Scholar 

  11. Keshavarz E, Ordokhani Y, Razzaghi M (2016) A numerical solution for fractional optimal control problems via Bernoulli polynomials. J Vib Control 22(18):1–15

    MathSciNet  MATH  Google Scholar 

  12. Behroozifar M, Habibi N (2018) A numerical approach for solving a class of fractional optimal control problems via operational matrix Bernoulli polynomials. J Vib Control 24(12):2494–2511

    MathSciNet  MATH  Google Scholar 

  13. Zaky MA, Tenreiro Machado JA (2017) On the formulation and numerical simulation of distributed-order fractional optimal control problems. Commun Nonlinear Sci Numer Simul 52:177–189

    MathSciNet  MATH  Google Scholar 

  14. Heydari MH, Hooshmandasl MR, Maalek Ghaini FM, Cattani C (2016) Wavelets method for solving fractional optimal control problems. Appl Math Comput 286:139–154

    MathSciNet  MATH  Google Scholar 

  15. Hosseinpour S, Nazemi AR (2016) Solving fractional optimal control problems with fixed or free final states by Haar wavelet collocation method. IMA J Math Control Inf 33(2):543–561

    MathSciNet  MATH  Google Scholar 

  16. Almeida R, Torres D (2015) A discrete method to solve fractional optimal control problems. Nonlinear Dyn 80:1811–1816

    MathSciNet  MATH  Google Scholar 

  17. Baleanu D, Jajarmi A, Hajipour M (2017) A new formulation of the fractional optimal control problems involving Mittag–Leffler nonsingular kernel. J Optim Theory Appl 157(3):718–737

    MathSciNet  MATH  Google Scholar 

  18. Jajarmi A, Hajipour M, Mohammadzadeh E, Baleanu D (2018) A new approach for the nonlinear fractional optimal control problems with external persistent disturbances. J Frankl Inst 355:3938–3967

    MathSciNet  MATH  Google Scholar 

  19. Agrawal OP, Defterli O, Baleanu D (2010) Fractional optimal control problems with several state and control variable. J Vib Control 16(3):1967–1976

    MathSciNet  MATH  Google Scholar 

  20. Tohidi E, Saberi Nik H (2015) A Bessel collocation method for solving fractional optimal control problems. Appl Math Model 39(2):455–465

    MathSciNet  MATH  Google Scholar 

  21. Bhrawy AH, Ezz-Eldien SS, Doha EH, Abdelkawy MA, Baleanu D (2017) Solving fractional optimal control problems within a Chebyshev–Legendre operational technique. Int J Control 90(6):1230–1244

    MathSciNet  MATH  Google Scholar 

  22. Doha EH, Bhrawy AH, Baleanu D, Ezz-Eldien SS, Hafez RM (2015) An efficient numerical scheme based on the shifted orthonormal Jacobi polynomials for solving fractional optimal control problems. Adv Differ Equ 15:1–17

    MathSciNet  MATH  Google Scholar 

  23. Dehghan M, Hamedi EA, Khosravian-Arab H (2016) A numerical scheme for the solution of a class of fractional variational and optimal control problems using the modified Jacobi polynomials. J Vib Control 22(6):1–13

    MathSciNet  MATH  Google Scholar 

  24. Rabiei K, Ordokhani Y, Babolian E (2017) The Boubaker polynomials and their application to solve fractional optimal control problems. Nonlinear Dyn 88(2):1013–1026

    MathSciNet  MATH  Google Scholar 

  25. Nemati A, Yousefi S, Soltanian F, Ardabili JS (2016) An efficient numerical solution of fractional optimal control problems by using the Ritz method and Bernstein operational matrix. Asian J Control 18(6):2272–2282

    MathSciNet  MATH  Google Scholar 

  26. Rahimkhani P, Ordokhani Y, Babolian E (2016) An efficient approximate method for solving delay fractional optimal control problems. Nonlinear Dyn 86(3):1649–1661

    MathSciNet  MATH  Google Scholar 

  27. Moradi L, Mohammadi F, Baleanu D (2019) A direct numerical solution of time-delay fractional optimal control problems by using Chelyshkov wavelets. J Vibr Control 25(2):1–15

    MathSciNet  Google Scholar 

  28. Bello Salati A, Shamsi F, Torres D (2019) Direct transcription methods based on fractional integral approximation formulas for solving nonlinear fractional optimal control problems. Commun Nonlinear Sci Numer Simul 67:334–350

    MathSciNet  MATH  Google Scholar 

  29. Sabermahani S, Ordokhani Y, Youse S (2019) Fractional-order Lagrange polynomials: an application for solving delay fractional optimal control problems.Trans Inst Meas Control 41:2997–3009

  30. Peng L, Zhou Y, Debbouche A (2019) Approximation techniques of optimal control problems for fractional dynamic systems in separable Hilbert spaces. Chaos Solitons Fract 118:234–241

    MathSciNet  MATH  Google Scholar 

  31. Hassani H, Tenreiro Machado JA, Naraghirad E (2019) Generalized shifted Chebyshev polynomials for fractional optimal control problems. Commun Nonlinear Sci Numer Simul 75:50–61

    MathSciNet  MATH  Google Scholar 

  32. Lotfi A (2019) Epsilon penalty method combined with an extension of the Ritz method for solving a class of fractional optimal control problems with mixed inequality constraints. Appl Numer Math 135:497–509

    MathSciNet  MATH  Google Scholar 

  33. Hosseinpour S, Nazemi AR, Tohidi E (2019) Muntz–Legendre spectral collocation method for solving delay fractional optimal control problems. J Comput Appl Math 351:344–363

    MathSciNet  MATH  Google Scholar 

  34. Rooh UA, Li A, Ali MM (2015) Fuzzy, neural network and expert systems methodologies and applications: a review. J Mob Multimed 11(1):157–176

    Google Scholar 

  35. Yu X, Zhou Z, Gao Q, Li D, Ríha K (2018) Infrared image segmentation using growing immune field and clone threshold. Infrared Phys Technol 88:184–193

    Google Scholar 

  36. Yu X, Ye X, Gao Q (2019) Pipeline image segmentation algorithm and heat loss calculation based ongene-regulated apoptosis mechanism. Int J Press Vessels Pip 172:329–336

    Google Scholar 

  37. Duan L, Fang X, Huang C (2017) Global exponential convergence in a delayed almost periodic nicholsons blowflies model with discontinuous harvesting. Math Methods Appl Sci 41(5):1954–1965

    MathSciNet  MATH  Google Scholar 

  38. Duan L, Huang L, Guo Z, Fang X (2017) Periodic attractor for reaction–diffusion high-order hopfield neural networks with time-varying delays. Comput Math Appl 73(2):233–245

    MathSciNet  MATH  Google Scholar 

  39. Yang C, Huang L, Li F (2018) Exponential synchronization control of discontinuous nonautonomous networks and autonomous coupled networks. Complexity 2018:1–10

    MATH  Google Scholar 

  40. Huang C, Su R, Cao J, Xiao S (2020) Asymptotically stable of high-order neutral cellular neural networks with proportional delays and D operators. Math Comput Simul 171:127–135

    MathSciNet  Google Scholar 

  41. Chen D, Zhang W, Cao J, Huang C (2020) Fixed time synchronization of delayed quaternion-valued memristor-based neural networks. Adv Differ Equ 2020:92

    MathSciNet  Google Scholar 

  42. Ghasemi S, Nazemi AR, Hosseinpour S (2017) Nonlinear fractional optimal control problems with neural network and dynamic optimization schemes. Nonlinear Dyn 89(4):2669–2682

    MathSciNet  MATH  Google Scholar 

  43. Kheyrinataj F, Nazemi AR (2020) Fractional power series neural network for solving delay fractional optimal control problems. Connect Sci 32:53–80

  44. Yavari M, Nazemi AR (2019) An efficient numerical scheme for solving fractional infinite-horizon optimal control problems. ISA Trans 94:108–118

    Google Scholar 

  45. Ghasemi S, Nazemi AR (2018) A neural network method based on Mittag-Leffer function for solving a class of fractional optimal control problems. AUT J Model Simul 50:211–218

  46. Kheyrinataj F, Nazemi AR (2020) Fractional Chebyshev functional link neural network-optimization method for solving delay fractional optimal control problems with Atangana-Baleanu derivative. Optim Control Appl Methods 41:808–832

    MathSciNet  Google Scholar 

  47. Yavari M, Nazemi AR (2020) On fractional infinite-horizon optimal control problems with a combination of conformable and Caputo-Fabrizio fractional derivatives. ISA Trans 101:78–90

    Google Scholar 

  48. Boulkaibet I, Belarbi K, Bououden S, Marwala T, Chadli M (2017) A new T–S fuzzy model predictive control for nonlinear processes. Expert Syst Appl 88:132–151

    Google Scholar 

  49. Zhu Q, Azar AT (2015) Complex system modelling and control through intelligent soft computations. Springer, Berlin

    MATH  Google Scholar 

  50. Wu ZG, Dong SH, Shi P, Su H, Huang T, Lu R (2017) Fuzzy-model-based nonfragile guaranteed cost control of nonlinear Markov jump systems. IEEE Trans Syst Man Cybern Syst 47(8):1–10

    Google Scholar 

  51. Mirzajani S, PourmahmoodAghababa M, Heydari A (2019) Adaptive T–S fuzzy control design for fractional-order systems withparametric uncertainty and input constraint. Fuzzy Sets Syst 365(15):22–39

    MATH  Google Scholar 

  52. Zhang HG, Yongbing Q (2001) Modeling, identification, and control of a class of nonlinear systems. IEEE Trans Fuzzy Syst 9(2):349–354

    MATH  Google Scholar 

  53. Zhang HG, Wang Z, Liu D (2003) Chaotifying fuzzy hyperbolic model using adaptive inverse optimal control approach. Int J Bifurc Chaos 12:32–43

    Google Scholar 

  54. Takagi T, Sugeno M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern 15(1):116–132

    MATH  Google Scholar 

  55. Dang QV et al (2017) Robust stabilizing controller design for Takagi–Sugeno fuzzy descriptor systems under state constraints and actuator saturation. Fuzzy Sets Syst 329:77–90

    MathSciNet  MATH  Google Scholar 

  56. Muthukumar P, Balasubramaniam P, Ratnavelu K (2016) T–S fuzzy predictive control for fractional order dynamical systems and its applications. Nonlinear Dyn 86(2):751–763

    MATH  Google Scholar 

  57. Dong J, Fu Y (2017) A design method for T–S fuzzy systems with partly immeasurable premise variables subject to actuator saturation. Neurocomputing 225:164–173

    Google Scholar 

  58. Shen H, Su L, Park JH (2017) Reliable mixed/passive control for T–S fuzzy delayed systems based on a semi-Markov jump model approach. Fuzzy Sets Syst 314:79–98

    MathSciNet  MATH  Google Scholar 

  59. Chen YY, Chang YT, Chen BS (2009) Fuzzy solutions to partial differential equations: adaptive approach. IEEE Trans Fuzzy Syst 17(1):116–127

    Google Scholar 

  60. Zhou Ya, Wan Xiaoxiao, Huang Chuangxia, Yang Xinsong (2020) Finite-time stochastic synchronization of dynamic networks with nonlinear coupling strength via quantized intermittent control. Appl Math Comput 376:125157

    MathSciNet  MATH  Google Scholar 

  61. Pakdaman M, Effati S (2016) Approximating the solution of optimal control problems by fuzzy systems. Neural Process Lett 43(3):667–686

    Google Scholar 

  62. Kosko B (1994) Fuzzy systems as universal approximators. IEEE Trans Comput 43(11):1329–1333

    MATH  Google Scholar 

  63. Buckley JJ (1992) Universal fuzzy controllers. Automatica 28:1245–1248

    MathSciNet  MATH  Google Scholar 

  64. Wang LX (1992) Fuzzy systems are universal approximators. In: Proceedings of the IEEE international conference on fuzzy systems. San Diego, pp 1163–1170

  65. Ying H (1994) Sufficient conditions on general fuzzy systems as function approximators. Automatica 30:521–525

    MATH  Google Scholar 

  66. Zeng XJ, Singh MG (1995) Approximation theory of fuzzy systems–MIMO case. IEEE Trans Fuzzy Syst 3(4):219–235

    Google Scholar 

  67. Kreinovich V, Nguyen HT, Yam Y (2000) Fuzzy systems are universal approximators for a smooth function and its derivatives. Int J Intell Syst 15(6):565–574

    MATH  Google Scholar 

  68. Zak SH (2003) Systems and control. Oxford University Press, Oxford

    Google Scholar 

  69. Zhang M, Zhang H (2006) Robust adaptive fuzzy control scheme for nonlinear system with uncertainty. J Control Theory Appl 4(2):209–216

    MathSciNet  MATH  Google Scholar 

  70. Zhang HG, Wang ZL, Li M, Quan B, Zhang MJ (2004) Generalized fuzzy hyperbolic model: a universal approximator. Acta Autom Sin 30(3):416–422

    MathSciNet  Google Scholar 

  71. Zhang JL, Zhang HG, Luo YH, Liang HJ (2013) Nearly optimal control scheme using adaptive dynamic programming based on generalized fuzzy hyperbolic model. Acta Autom Sin 39(2):142–148

    MathSciNet  MATH  Google Scholar 

  72. Sun Q, Wang Q, Yang J, Qiu Y, Zhang H (2014) Chaotic dynamics in smart grid and suppression scheme via generalized fuzzy hyperbolic model. Math Probl Eng 2014:Article ID 761271

  73. Cui Y, Zhang HG, Wang Y, Gao W (2016) Adaptive control for a class of uncertain strict-feedback nonlinear systems based on a generalized fuzzy hyperbolic model. Fuzzy Sets Syst 302:52–64

    MathSciNet  MATH  Google Scholar 

  74. Zhang H, Liu D (2006) Fuzzy modeling and fuzzy control. Springer, Berlin

    MATH  Google Scholar 

  75. ZhangM, Zhang H and Liu D (2004) A generalized fuzzy hyperbolicmodeling and control scheme. IEEE Int Conf Fuzzy Syst 3:1203–1207

  76. Zhang M, Zhang H (2005) Modeling and control based on generalized fuzzy hyperbolic model. In: American control conference (2005)

  77. Mortezaee M, Ghovatmand M, Nazemi A (2020) Solving variable-order fractional differential algebraic equations via generalized fuzzy hyperbolic model with application in electric circuit modeling. Soft Comput. https://doi.org/10.1007/s00500-020-04969-7

  78. Yepez-Martinez H, Gomez-Aguilar JF (2019) A new modified definition of Caputo–Fabrizio fractional-order derivative and their applications to the multi step homotopy analysis method. J Comput Appl Math 346:247–260

    MathSciNet  MATH  Google Scholar 

  79. Yildiz TA, Jajarmi A, Yildiz B, Baleanu D (2019) New aspects of time fractional optimal control problems within operators with nonsingular kernel. Discrete Continu Dyn Syst 13:407–428

    MathSciNet  MATH  Google Scholar 

  80. Bastos N (2018) Calculus of variations involving Caputo–Fabrizio fractional differentiation. Stat Optim Inf Comput 6:12–21

    MathSciNet  Google Scholar 

  81. Caputo M, Fabrizio M (2015) A new definition of fractional derivative without singular kernel Progr. Fract Differ Appl 1(2):73–85

    Google Scholar 

  82. Atanacković TM, Pilipović S, Zorica D (2018) Properties of the Caputo–Fabrizio fractional derivative and its distributional settings. Fract Calc Appl Anal 21(1):29–44

    MathSciNet  MATH  Google Scholar 

  83. Bazaraa MS, Sherali HD, Shetty CM (2006) Nonlinear programming—theory and algorithms, 3rd edn. Wiley, NJ, p 2006

    MATH  Google Scholar 

  84. Nocedal J, Wright S (2006) Numerical optimization, 2nd edn. Springer, NewYork

    MATH  Google Scholar 

  85. Lee KY, El-Sharkawi KY (2008) Modern heuristic optimization techniques: theory and applications to power systems. IEEE Press Series Power Eng

  86. Mei W, Bullo W (2017) LaSalle invariance principle for discrete-time dynamical systems: a concise and self-contained tutorial. arXiv:1710.03710

Download references

Funding

This study was not funded by any grant.

Author information

Authors and Affiliations

  1. Faculty of Mathematical Sciences, Shahrood University of Technology, Shahrood, Iran

    Marzieh Mortezaee, Mehdi Ghovatmand & Alireza Nazemi

Authors
  1. Marzieh Mortezaee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mehdi Ghovatmand
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alireza Nazemi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mehdi Ghovatmand.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mortezaee, M., Ghovatmand, M. & Nazemi, A. An Application of Generalized Fuzzy Hyperbolic Model for Solving Fractional Optimal Control Problems with Caputo–Fabrizio Derivative. Neural Process Lett 52, 1997–2020 (2020). https://doi.org/10.1007/s11063-020-10334-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-020-10334-4

Keywords

Search

Navigation