Abstract
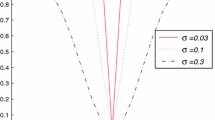
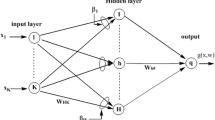
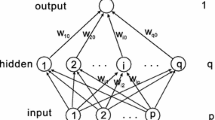
\(L_0\) regularization is an ideal pruning method for neural networks as it can generate the sparsest results of all \(L_p\) regularization method. However, the solving of \(L_0\) regularization is an NP-hard problem, and the existing training algorithm with \(L_0\) regularization can only prune the networks weights, but not neurons. To this end, in this paper we propose a batch gradient training method with smoothing Group \(L_0\) regularization (\(\hbox {BGSGL}_0\)). \(\hbox {BGSGL}_0\) not only overcomes the NP-hard nature of the \(L_0\) regularizer, but also prunes the network from the neuron level. The working mechanism for \(\hbox {BGSGL}_0\) to prune hidden neurons is analysed, and the convergence is theoretically established under mild conditions. Simulation results are provided to validate the theoretical finding and the the superiority of the proposed algorithm.


Similar content being viewed by others
References
Zhang H, Wang J, Sun Z, Zurada JM, Pal NR (2020) Feature selection for neural networks using Group Lasso regularization. IEEE Trans Knowl Data Eng 32(4):659–673
Liu T, Xiao J, Huang Z, Kong E, Liang Y (2019) BP neural network feature selection based on Group Lasso regularization. Proc. Chin. Autom. Congr. 2786-2790
Alemu HZ, Zhao J, Li F, Wu W (2019) Group \(L_{1/2}\) regularization for pruning hidden layer nodes of feedforward neural networks. IEEE Access 7:9540–9557
Augasta MG, Kathirvalavakumar T (2011) A novel pruning algorithm for optimizing feedforward neural network of classifification problems. Neural Process Lett 34:241–258
Zeng XQ, Yeung DS (2006) Hidden neuron pruning of multilayer perceptrons using a quantified sensitivity measure. Neurocomputing 69:825–837
Wang J, Chang Q, Chang Q, Liu Y, Pal NR (2019) Weight noise injection-based MLPs with Group Lasso penalty: asymptotic convergence and application to node pruning. IEEE T Cybern 49:4346–4364
Wang J, Xu C, Yang X, Zurada JM (2018) A novel pruning algorithm for smoothing feedforward neural networks based on Group Lasso method. IEEE Trans Neural Netw Learn Syst 29(5):2012–2024
Dheeru D, Taniskidou EK (2017) UCI machine learning repository. Comput. Sci. Univ. California, Irvine, CA, USA, Tech. Rep, School Inf
Moody JO, Antsaklis PJ (1996) The dependence identification neural network construction algorithm. IEEE Trans Neural Netw 7:3–15
Augasta MG, Kathirvalavakumar T (2013) Pruning algorithms of neural networks a comparative study. Central Eur J Comput Sci 3:105–115
Reed R (1993) Pruning algorithms: a survey. IEEE Trans Neural Netw 4:740–747
Wang XY, Wang J, Zhang K, Lin F, Chang Q (2021) Convergence and objective functions of noise-injected multilayer perceptrons with hidden multipliers. Neurocomputing 452:796–812
Xu ZB, Chang XY, Xu FM, Zhang H (2012) \(L_{1/2}\) regularization: a thresholding representation theory and a fast solver. IEEE Trans Neural Netw Learn Syst 23(7):1013–27
Miao C, Yu H (2016) Alternating iteration for \(L_p(0 < p)\) regularized CT reconstruction. IEEE Access 4:4355–4363
Treadgold NK, Gedeon TD (1998) Simulated annealing and weight decay in adaptive learning: the SARPROP algorithm. IEEE Trans Neural Netw 9(4):662–8
Wu W, Fan Q, Zurada JM, Wang J, Yang D, Liu Y (2014) Batch gradient method with smoothing \(L_{1/2}\) regularization for training of feedforward neural networks. Neural Netw 50:72–78
Zhang HS, Zhang Y, Zhu S, Xu DP (2020) Deterministic convergence of complex mini-batch gradient learning algorithm for fully complex-valued neural networks. Neurocomputing 407:185–193
Wu W, Wang J, Cheng MS, Li ZX (2011) Convergence analysis of online gradient method for BP neural networks. Neural Netw 24(1):91–8
Zhang HS, Tang YL (2017) Online gradient method with smoothing \(L_0\) regularization for feedforward neural networks. Neurocomputing 224:1–8
Wang J, Wu W, Zurada JM (2011) Deterministic convergence of conjugate gradient mehtod for feedforward neural networks. Neurocomputing 74:2368–2376
Zhang HS, Wu W, Yao MC (2012) Boundedness and convergence of batch back-propagation algorithm with penalty for feedforward neural networks. Neurocomputing 89:141–146
Yang DK, Liu Y (2018) \(L_{1/2}\) regularization learning for smoothing interval neural networks: Algorithms and convergence analysis. Neurocomputing 272:122–129
Kurkova V, Sanguineti M (2001) Bounds on rates of variable-basis and neural-network approximation. IEEE Trans Inf Theory 47(6):2659–2665
Gnecco G, Sanguineti M (2011) On a variational norm tailored to variable-basis approximation schemes. IEEE Trans Inf Theory 57(1):549–558
Xu ZB, Zhang H, Wang Y, Chang XY, Liang Y (2010) \(L_{1/2}\) regularization. Sci China-Inf Sci 6:1159–1169
Kurt H, Maxwell S, Halbert W (1989) Multilayer feedforward networks are universal approximators. Neural Netw 2:359–366
Li F, Zurada JM, Wu W (2018) Smooth Group \(L_{1/2}\) regularization for input layer of feedforward neural networks. Neurocomputing 314:109–119
Li F, Zurada JM, Liu Y, Wu W (2017) Input layer regularization of multilayer feedforward neural networks. IEEE Access 5:10979–10985
Wang J, Zhang H, Wang J, Pu YF, Pal NR (2021) Feature selection using a neural network with Group Lasso regularization and controlled redundancy. IEEE Trans Neural Netw Learn Syst 32(3):1110–1123
Scardapane S, Comminiello D, Hussain A, Uncini A (2017) Group sparse regularization for deep neural networks. Neurocomputing 241:81–89
Xie XT, Zhang HQ, Wang Chang Q, Wang J, Pal NR (2020) Learning optimized structure of neural networks by hidden node pruning with \(L_1\) regularization. IEEE T Cybern 50:1333–1346
Formanek A, Hadhzi D (2019) Compressing convolutional neural networks by \(L_0\) regularization. Proceeding International Conference on Control, Artificial Intelligence, Robotics & Optimization pp 155-162
Scardapane S, Comminiello D, Hussain A, Uncini A (2017) Group sparse regularization for deep neural networks. Neurocomputing 241:81–89
Zhang HS, Tang YL, Liu XD (2015) Batch gradient training method with smoothing regularization for \(L_0\) feedforward neural networks. Neural Comput & Applic 26(2):383–390
Xie Q, Li C, Diao B, An Z, Xu Y (2019) \(L_0\) regularization based fine-grained neural network pruning method. Proc. Int. Conf. Electron. Comput. Artif. Intell. p 11:1-4
Wang J, Cai Q, Zurada JM, Chang Q, Zurada JM (2017) Convergence analyses on sparse feedforward neural networks via Group Lasso regularization. Inf Sci 381:250–269
Fan Q, Peng J, Li H, Lin S (2021) Convergence of a gradient-based learning algorithm with penalty for ridge polynomial neural networks. IEEE Access 9:28742–28752
Kang Q, Fan Q, Zurada JM (2021) Deterministic convergence analysis via smoothing Group Lasso regularization and adaptive momentum for Sigma-Pi-Sigma neural network. Inf Sci 553:66–82
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Nos. 61671099, 62176051).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In this appendix, we present the proof of Theorem 1. For brevity, we list the following constants which will be used in the sequel.
For the sake of simplicity, we also define the following notations
The following two lemmas are crucial to our convergence analysis.
Lemma 1
Suppose Assumptions (A1) and (A2) are valid, then we have
where the constant \(C_5\) is defined in (20), \(m=1,2,\dots ,M\), \(l=1,2,\dots ,L\), and \(j=1,2,\dots ,J\).
Proof
Using (2) we have
Using Lagrangian mean value theorem, Assumption (A1), and Eq.(23), we have:
where \(t^{m,j}_l\) is between \({{\textbf {v}}}^{m+1}_l{{\textbf {x}}}^j\) and \({{\textbf {v}}}^{m}_l{{\textbf {x}}}^j\) . \(\square \)
Lemma 2
(See Lemma 3 in [21]) Let \(F:\varPhi \subset R^k \rightarrow R^q(k,q\ge 1)\) be continuous for a bounded closed region \(\varPhi \), and \(\varOmega = \{{{\textbf {z}}}\in \varPhi : F({{\textbf {z}}})=0\}\). The projection of \(\varOmega \) on each coordinate axis does not contain any interior point. Let the sequence \(\{{{\textbf {z}}}^m\}\) satisfy
Then, there exists a unique \({{\textbf {z}}}^*\in \varOmega \) such that \(\lim \limits _{m \rightarrow \infty }{{\textbf {z}}}^m={{\textbf {z}}}^*\).
\({\textbf {Proof to (1) of theorem}}\) 1. Applying Taylor formula to the cost function defined in (11), we have
where \(t_0^{j,q}\) is between \({{\textbf {u}}}^{m+1}_{r_q}{{\textbf {F}}}^{m+1,j}\) and \({{\textbf {u}}}^{m}_{r_q}{{\textbf {F}}}^{m,j}\).
By (21) and Taylor formula, we have
Substituting (27) into (26), we have
where
Combining (13)-(15), (27)-(29), we have
Applying Taylor formula, we have
where \(\xi ^{m}_l\) is between \(\parallel {{\textbf {w}}}^{m+1}_l\parallel ^2\) and \(\parallel {{\textbf {w}}}^{m}_l\parallel ^2\).
In order to give a further estimation of the Eq. (29), we apply the triangular inequality and obtain
and
Combining the above two equations, we have
where \(C_1=\max \{\frac{JQC^2_5}{2}(C_3+ C_4+2C_3C^2_4),\frac{JC_3}{2}(1+2C^2_5)\}\).
Substituting (31)-(34) into (30), we have
where \(C_7=C_6+\sup _{t\in R}h'_{\sigma }(t)\).
Thus, if the learning rate \(\eta \) satisfies \(0<\eta < \frac{1}{C_7\lambda +C_1}\), then we have \(E({{\textbf {w}}}^{m+1})\le E({{\textbf {w}}}^{m})\). This ends the proof for the monotonicity of the error function.
\({\textbf {Proof to (2) of theorem}}\) 1. As \(E({{\textbf {w}}}^m)\) is monotonically decreasing and \(E({{\textbf {w}}}^m)\ge 0\), there exists a constant \(E^*\ge 0\) such that
\({\textbf {Proof to (3) of theorem}}\) 1. Let \(\beta = \frac{1}{\eta }- C_7\lambda - C_1>0\). By (35), we have
Since \(E({{\textbf {w}}}^{m}) \ge 0\) holds for any \(m\ge 1\), we have
Considering \(E({{\textbf {w}}}^{m}) \ge 0\), let \(m\rightarrow \infty \), then we have
Then we have
\({\textbf {Proof to (4) of theorem}}\) 1. Obviously \(\parallel E_{{{\textbf {w}}}}({{\textbf {w}}}) \parallel \) is a continuous function under Assumptions \((A1)-(A4)\). Using (12), we have
By virtue of Lemma 2, there exists a constant \({{\textbf {w}}}^*\) such that \(\lim \limits _{m\rightarrow \infty }{{\textbf {w}}}^m={{\textbf {w}}}^*\). This completes the proof to (4) of Theorem 1.
This completes the proof of Theorem 1.
Rights and permissions
About this article
Cite this article
Zhang, Y., Wei, J., Xu, D. et al. Batch Gradient Training Method with Smoothing Group \(L_0\) Regularization for Feedfoward Neural Networks. Neural Process Lett 55, 1663–1679 (2023). https://doi.org/10.1007/s11063-022-10956-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-022-10956-w