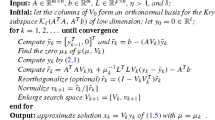Abstract
Tikhonov regularization often is applied with a finite difference regularization operator that approximates a low-order derivative. This paper proposes the use of orthogonal projections as regularization operators, e.g., with the same null space as commonly used finite difference operators. Applications to iterative and SVD-based methods for Tikhonov regularization are described. Truncated iterative and SVD methods are also considered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Björck, Å.: Numerical Methods for Least Squares Problems. SIAM, Philadelphia (1996)
Calvetti, D., Lewis, B., Reichel, L.: On the choice of subspace for iterative methods for linear discrete ill-posed problems. Int. J. Appl. Math. Comput. Sci. 11, 1069–1092 (2001)
Calvetti, D., Reichel, L.: Tikhonov regularization of large linear problems. BIT 43, 263–283 (2003)
Eldén, L.: Algorithms for the regularization of ill-conditioned least squares problems. BIT 17, 134–145 (1977)
Eldén, L.: A weighted pseudoinverse, generalized singular values, and constrained least squares problems. BIT 22, 487–501 (1982)
Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems. Kluwer, Dordrecht (1996)
Golub, G.H., von Matt, U.: Tikhonov regularization for large scale problems. In: Golub, G.H., Lui, S.H., Luk, F., Plemmons, R. (eds.) Workshop on Scientific Computing, pp. 3–26. Springer, New York (1997)
Hanke, M.: Conjugate Gradient Type Methods for Ill-Posed Problems. Longman, Essex (1995)
Hanke, M., Hansen, P.C.: Regularization methods for large-scale problems. Surv. Math. Ind. 3, 253–315 (1993)
Hansen, P.C.: Regularization tools: a Matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 6, 1–35 (1994) (Software is available in Netlib at the web site http://www.netlib.org)
Hansen, P.C.: Rank-Deficient and Discrete Ill-Posed Problems. SIAM, Philadelphia (1998)
Paige, C.C., Saunders, M.A.: LSQR: An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. 8, 43–71 (1982)
Phillips, D.L.: A technique for the numerical solution of certain integral equations of the first kind. J. ACM 9, 84–97 (1962)
Reichel, L., Ye, Q.: Breakdown-free GMRES for singular systems. SIAM J. Matrix Anal. Appl. 26, 1001–1021 (2005)
Author information
Authors and Affiliations
Corresponding author
Additional information
Research of L. Reichel was supported in part by an OBR Research Challenge Grant.
Research of F. Sgallari was supported in part by PRIN 2004 grant 2004014411-005.
Rights and permissions
About this article
Cite this article
Morigi, S., Reichel, L. & Sgallari, F. Orthogonal projection regularization operators. Numer Algor 44, 99–114 (2007). https://doi.org/10.1007/s11075-007-9080-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-007-9080-8