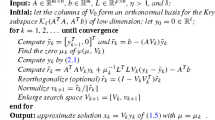Skip to main content
SpringerLink
Log in

On the choice of solution subspace for nonstationary iterated Tikhonov regularization

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

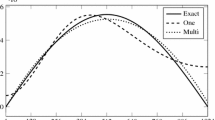
Tikhonov regularization is a popular method for the solution of linear discrete ill-posed problems with error-contaminated data. Nonstationary iterated Tikhonov regularization is known to be able to determine approximate solutions of higher quality than standard Tikhonov regularization. We investigate the choice of solution subspace in iterative methods for nonstationary iterated Tikhonov regularization of large-scale problems. Generalized Krylov subspaces are compared with Krylov subspaces that are generated by Golub–Kahan bidiagonalization and the Arnoldi process. Numerical examples illustrate the effectiveness of the methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bianchi, D., Buccini, A., Donatelli, M., Serra–Capizzano, S.: Iterated fractional Tikhonov regularization. Inverse Prob. 31, 055005 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  2. Björck, Å.: A bidiagonalization algorithm for solving large and sparse ill-posed systems of linear equations. BIT 28, 659–670 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  3. Björck, Å.: Numerical Methods in Matrix Computations. Springer, New York (2015)

    Book  MATH  Google Scholar 

  4. Calvetti, D., Hansen, P.C., Reichel, L.: L-curve curvature bounds via Lanczos bidiagonalization. Electron. Trans. Numer. Anal. 14, 20–35 (2002)

    MathSciNet  MATH  Google Scholar 

  5. Calvetti, D., Morigi, S., Reichel, L., Sgallari, F.: Tikhonov regularization and the L-curve for large, discrete ill-posed problems. J. Comput. Appl. Math. 123, 423–446 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  6. Daniel, J.W., Gragg, W.B., Kaufman, L., Stewart, G.W.: Reorthogonalization and stable algorithms for updating the Gram–Schmidt QR factorization. Math. Comp. 30, 772–795 (1976)

    MathSciNet  MATH  Google Scholar 

  7. Donatelli, M., Hanke, M.: Fast nonstationary preconditioned iterative methods for ill-posed problems, with application to image deblurring. Inverse Prob. 29, 095008 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Dykes, L., Noschese, S., Reichel, L.: Rescaling the GSVD with application to ill-posed problems. Numer. Algorithms 68, 531–545 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Dykes, L., Reichel, L.: A family of range restricted iterative methods for linear discrete ill-posed problems. Dolomites Research Notes on Approximation 6, 27–36 (2013)

    MATH  Google Scholar 

  10. Eldén, L.: A weighted pseudoinverse, generalized singular values, and constrained least squares problems. BIT 22, 487–502 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  11. Engl, H.W.: On the choice of the regularization parameter for iterated Tikhonov regularization of ill-posed problems. J. Approx. Theory 49, 55–63 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  12. Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems. Kluwer, Dordrecht (1996)

    Book  MATH  Google Scholar 

  13. Gazzola, S., Novati, P., Russo, M.R.: On Krylov projection methods and Tikhonov regularization. Electron. Trans. Numer. Anal. 44, 83–123 (2015)

    MathSciNet  MATH  Google Scholar 

  14. Hanke, M., Groetsch, C.W.: Nonstationary iterated Tikhonov regularization. J. Optim. Theory Appl. 436, 37–53 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  15. Hansen, P.C.: Rank-Deficient and Discrete Ill-Posed Problems. SIAM, Philadelphia (1998)

    Book  Google Scholar 

  16. Hansen, P.C.: Regularization tools version 4.0 for Matlab 7.3. Numer. Algorithms 46, 189–194 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  17. Hochstenbach, M.E., Reichel, L.: An iterative method for Tikhonov regularization with a general linear regularization operator. J. Integral Equations Appl. 22, 463–480 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Huang, G., Reichel, L., Yin, F.: Projected nonstationary iterated Tikhonov regularization. BIT (in press)

  19. Kilmer, M.E., Hansen, P.C., Español, M.I.: A projection-based approach to general-form Tikhonov regularization. SIAM J. Sci. Comput. 29, 315–330 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  20. Lampe, J., Reichel, L., Voss, H.: Large-scale Tikhonov regularization via reduction by orthogonal projection. Linear Algebra Appl. 436, 2845–2865 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  21. Lampe, J., Voss, H.: A fast algorithm for solving regularized total least squares problems. Electron. Trans. Numer. Anal. 31, 12–24 (2008)

    MathSciNet  MATH  Google Scholar 

  22. Lampe, J., Voss, H.: Large-scale dual regularized total least squares. Electron. Trans. Numer. Anal. 42, 13–40 (2014)

    MathSciNet  MATH  Google Scholar 

  23. Morigi, S., Reichel, L., Sgallari, F.: Orthogonal projection regularization operators. Numer. Algorithms 44, 99–114 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Neuman, A., Reichel, L., Sadok, H.: Implementations of range restricted iterative methods for linear discrete ill-posed problems. Linear Algebra Appl. 436, 3974–3990 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  25. O’Leary, D.P., Simmons, J.A.: A bidiagonalization-regularization procedure for large scale discretizations of ill-posed problems. SIAM J. Sci. Stat. Comput. 2, 474–489 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  26. Paige, C.C., Saunders, M.A.: LSQR: an algorithm for sparse linear equations and sparse least squares problems. ACM Trans. Math. Softw. 8, 43–71 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  27. Reichel, L., Sgallari, F., Ye, Q.: Tikhonov regularization based on generalized Krylov subspace methods. Appl. Numer. Math. 62, 474–489 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  28. Reichel, L., Yu, X.: Matrix decompositions for Tikhonov regularization. Electron. Trans. Numer. Anal. 43, 223–243 (2015)

    MathSciNet  MATH  Google Scholar 

  29. Saad, Y.: Iterative Methods for Sparse Linear Systems. SIAM, Philadelphia (2003)

    Book  MATH  Google Scholar 

  30. Shaw Jr., C.B.: Improvements of the resolution of an instrument by numerical solution of an integral equation. J. Math. Anal. Appl. 37, 83–112 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  31. Voss, H.: An Arnoldi method for nonlinear eigenvalue problems. BIT 44, 387–401 (2004)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Geomathematics Key Laboratory of Sichuan, Chengdu University of Technology, Chengdu, 610059, People’s Republic of China

    Guangxin Huang & Feng Yin

  2. College of Management Science, Chengdu University of Technology, Chengdu, 610059, People’s Republic of China

    Guangxin Huang

  3. Department of Mathematical Sciences, Kent State University, Kent, OH, 44242, USA

    Lothar Reichel

  4. School of Sciences, Sichuan University of Science and Engineering, Zigong, 643000, People’s Republic of China

    Feng Yin

Authors
  1. Guangxin Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lothar Reichel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Feng Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lothar Reichel.

Additional information

Dedicated to Gerhard Opfer on the occasion of his 80th birthday.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, G., Reichel, L. & Yin, F. On the choice of solution subspace for nonstationary iterated Tikhonov regularization. Numer Algor 72, 1043–1063 (2016). https://doi.org/10.1007/s11075-015-0079-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-015-0079-2

Keywords

Mathematics Subject Classification (2010)

Search

Navigation